
Dieser Artikel führt Sie hauptsächlich in die relevanten Informationen zur Verwendung von Python zur Lösung des Doppelfeder-Masse-Energie-Systems in der Physik ein. Der Artikel stellt es detailliert anhand von Beispielcode vor, der einen gewissen Referenz-Lernwert für jedermanns Studium oder Arbeit hat ., Freunde, die es brauchen, folgen Sie bitte dem Herausgeber, um gemeinsam zu lernen.
Vorwort
Dieser Artikel stellt hauptsächlich den relevanten Inhalt zur Verwendung von Python zur Lösung des Doppelfeder-Masse-Energie-Systems in der Physik vor Bitte beziehen Sie sich darauf. Ich werde im Folgenden nicht viel mehr sagen. Schauen wir uns die ausführliche Einleitung an.
Das physikalische Modell ist wie folgt:
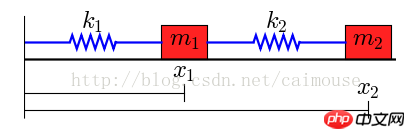
In diesem System gibt es zwei Objekte, ihre Massen Sie sind m1 bzw. m2, durch zwei Federn miteinander verbunden, das Teleskopsystem ist k1 und k2 und das linke Ende ist fest. Unter der Annahme, dass keine äußere Kraft einwirkt, betragen die Längen der beiden Federn L1 und L2.
Da die beiden Objekte Schwerkraft haben, entsteht auf der Ebene Reibung und die Reibungskoeffizienten sind b1 bzw. b2. Die Differentialgleichung kann also wie folgt geschrieben werden:
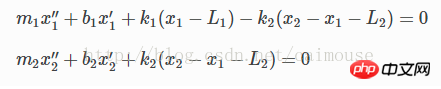
Dies ist eine Differentialgleichung zweiter Ordnung. Um sie mit Python zu lösen, muss sie in a umgewandelt werden Differentialgleichung erster Ordnung. Daher werden die folgenden zwei Variablen eingeführt:

Diese beiden entsprechen der Bewegungsgeschwindigkeit. Durch die Operation kann es wie folgt geändert werden:
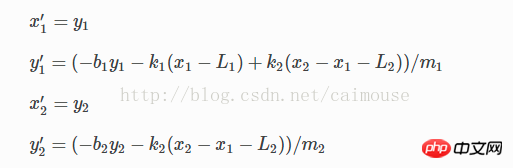
Zu diesem Zeitpunkt kann die lineare Gleichung in ein Vektorarray geändert werden und Python kann zum Definieren von
verwendet werdenDer Code lautet wie folgt:
# Use ODEINT to solve the differential equations defined by the vector field
from scipy.integrate import odeint
def vectorfield(w, t, p):
"""
Defines the differential equations for the coupled spring-mass system.
Arguments:
w : vector of the state variables:
w = [x1,y1,x2,y2]
t : time
p : vector of the parameters:
p = [m1,m2,k1,k2,L1,L2,b1,b2]
"""
x1, y1, x2, y2 = w
m1, m2, k1, k2, L1, L2, b1, b2 = p
# Create f = (x1',y1',x2',y2'):
f = [y1,
(-b1 * y1 - k1 * (x1 - L1) + k2 * (x2 - x1 - L2)) / m1,
y2,
(-b2 * y2 - k2 * (x2 - x1 - L2)) / m2]
return f
# Parameter values
# Masses:
m1 = 1.0
m2 = 1.5
# Spring constants
k1 = 8.0
k2 = 40.0
# Natural lengths
L1 = 0.5
L2 = 1.0
# Friction coefficients
b1 = 0.8
b2 = 0.5
# Initial conditions
# x1 and x2 are the initial displacements; y1 and y2 are the initial velocities
x1 = 0.5
y1 = 0.0
x2 = 2.25
y2 = 0.0
# ODE solver parameters
abserr = 1.0e-8
relerr = 1.0e-6
stoptime = 10.0
numpoints = 250
# Create the time samples for the output of the ODE solver.
# I use a large number of points, only because I want to make
# a plot of the solution that looks nice.
t = [stoptime * float(i) / (numpoints - 1) for i in range(numpoints)]
# Pack up the parameters and initial conditions:
p = [m1, m2, k1, k2, L1, L2, b1, b2]
w0 = [x1, y1, x2, y2]
# Call the ODE solver.
wsol = odeint(vectorfield, w0, t, args=(p,),
atol=abserr, rtol=relerr)
with open('two_springs.dat', 'w') as f:
# Print & save the solution.
for t1, w1 in zip(t, wsol):
out = '{0} {1} {2} {3} {4}\n'.format(t1, w1[0], w1[1], w1[2], w1[3]);
print(out)
f.write(out);Geben Sie die Ergebnisse hier in die Datei two_springs.dat aus. Schreiben Sie dann ein Programm, um die Daten als Bild anzuzeigen. Sie können das Papier veröffentlichen. Der Code lautet wie folgt:
# Plot the solution that was generated from numpy import loadtxt from pylab import figure, plot, xlabel, grid, hold, legend, title, savefig from matplotlib.font_manager import FontProperties t, x1, xy, x2, y2 = loadtxt('two_springs.dat', unpack=True) figure(1, figsize=(6, 4.5)) xlabel('t') grid(True) lw = 1 plot(t, x1, 'b', linewidth=lw) plot(t, x2, 'g', linewidth=lw) legend((r'$x_1$', r'$x_2$'), prop=FontProperties(size=16)) title('Mass Displacements for the\nCoupled Spring-Mass System') savefig('two_springs.png', dpi=100)
Schließlich überprüfen wir das Ausgabe-PNG Bild wie folgt:
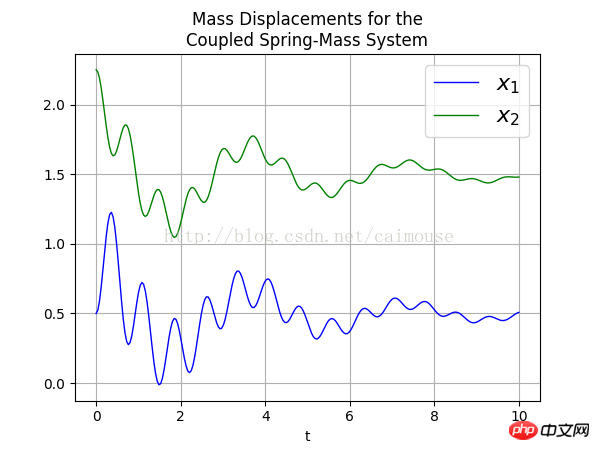
Zusammenfassung
Das obige ist der detaillierte Inhalt vonPython-Codebeispiel zur Lösung des Doppelfeder-Masse-Energie-Systems in der Physik. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




