Schnelle Sortiermethode
HTML5 Academy-Code Craftsman: In den vorherigen Ausgaben von „Algorithm Journey“ habe ich Ihnen die Blasensortiermethode und die Auswahlsortiermethode vorgestellt. Beide haben eine Zeitkomplexität von O (n^ 2) „Langsame“ Sortierung. Heute möchte ich Ihnen den am weitesten verbreiteten und schnellsten Sortieralgorithmus unter den verschiedenen Sortieralgorithmen vorstellen – die schnelle Sortierung [durchschnittliche Zeitkomplexität beträgt O (n logn)].
Tipps 1: Die Grundkenntnisse zu „Algorithmus“ und „Sortierung“ wurden im vorherigen Abschnitt „Auswahlsortiermethode“ ausführlich erläutert. Sie können auf den entsprechenden Artikellink am Ende des Artikels klicken, um ihn anzuzeigen es, und ich werde es hier nicht wiederholen.
Tipps 2: Sofern nicht anders angegeben, erfolgt die Schnellsortierung in diesem Artikel von klein nach groß.
Prinzip der Schnellsortierung
Schnellsortierung ist eine Partitionierungs- und Austauschsortierung. Sie verwendet die Divide-and-Conquer-Strategie, die üblicherweise als Divide-and-Conquer-Methode bezeichnet wird.
Teile-und-Herrsche-Methode
Grundidee: Zerlegen Sie das ursprüngliche Problem in mehrere kleinere Unterprobleme, die jedoch ähnliche Strukturen wie das ursprüngliche Problem haben. Lösen Sie diese Teilprobleme rekursiv und kombinieren Sie dann die Ergebnisse dieser Teilprobleme mit den Ergebnissen des ursprünglichen Problems.
Grundprinzip
Wählen Sie eine beliebige Zahl aus der Folge als „Basis“ aus.
Alle Zahlen, die kleiner als die „Basis“ sind, werden nach links von der „Basis“ verschoben. ; Zahlen, die größer oder gleich der „Grundlinie“ sind, werden nach rechts von der „Grundlinie“ verschoben.
Nach Abschluss dieser Verschiebung befindet sich die „Grundlinie“ in der Mitte der beiden Sequenzen und wird nicht angezeigt mehr an der nachfolgenden Sortierung teilnehmen;
Wiederholen Sie die obigen Schritte für die beiden Teilsequenzen links und rechts der „Grundlinie“, bis in allen Teilsequenzen nur noch eine Zahl übrig bleibt.
Prinzipielle Darstellung
Die vorhandene Reihenfolge ist [8, 4, 7, 2, 0, 3, 1]. Im Folgenden wird gezeigt, wie sie mit der Schnellsortierungsmethode sortiert wird.
Aufschlüsselung der Schritte zur Implementierung der Schnellsortierung
Wählen Sie „Baseline“ aus und trennen Sie es vom ursprünglichen Array
Rufen Sie den Index der ab Geben Sie zunächst den Basiswert ein und verwenden Sie dann die Splice-Array-Methode, um den Benchmark-Wert zu erhalten.
Tipps: In diesem Beispiel ist der Indexwert des Benchmarks = parseInt (Sequenzlänge / 2)
Tipps: Die Spleißmethode ändert das Original Array. Beispiel: arr = [1, 2, 3]; Der Basisindexwert ist 1, der Basiswert ist 2 und das ursprüngliche Array wird zu arr = [1, 3];
Durchlaufen Sie die Sequenz und teilen Sie sie auf die Sequenz
Vergleichen Sie die Größe mit der „Grundlinie“ und teilen Sie sie in zwei Teilsequenzen auf
Zahlen, die kleiner als die „Grundlinie“ sind, werden im Array leftArr gespeichert, und Zahlen, die größer oder gleich der sind „baseline“ werden im rightArr-Array gespeichert
Tipps: Natürlich können Sie auch die Zahl kleiner oder gleich der „baseline“ in leftArr und die Zahl speichern größer als die „Grundlinie“ in rightArr
Da die Sequenz durchlaufen werden muss, vergleichen Sie jede Zahl mit der „Benchmark“, sodass Sie zur Implementierung die for-Anweisung verwenden müssen
Rekursiver Aufruf, Durchlaufen der Teilsequenz und Kombinieren der Ergebnisse der Teilsequenz
Definieren Sie eine Funktion, deren formale Parameter zum Empfangen der Array-
Funktion verwendet werden quickSort(arr) { };
Rekursive Aufrufdurchquerung implementieren Sequenz, verwenden Sie die Concat-Array-Methode, um die Ergebnisse der Teilsequenz zu kombinieren
Bestimmen Sie die Länge der Teilsequenz
Wenn während des rekursiven Aufrufs die Länge der Teilsequenz gleich 1 ist, stoppen Sie den rekursiven Aufruf und geben Sie das aktuelle Array zurück.
Vollständiger Code der Schnellsortierung
Effizienz der Schnellsortierung
Zeitkomplexität
Worst-Case-Szenario: Die jeweils ausgewählte „Basislinie“ ist die kleinste/größte Zahl in der Reihenfolge. Diese Situation ähnelt der Blasensortierungsmethode (es kann jeweils nur eine Zahl [Basisliniennummer] ermittelt werden). ), die zeitliche Komplexität beträgt O(n^2)
Bester Fall: Die jeweils ausgewählte „Basislinie“ ist die mittlere Zahl in der Sequenz (es ist der Median, nicht die Position) Mitte), dann die Die aktuelle Sequenz wird jeweils in zwei gleich lange Teilsequenzen unterteilt. Zu diesem Zeitpunkt gibt es beim ersten Mal zwei Teilfolgen n/2 und n/2, beim zweiten Mal vier Teilfolgen n/4, n/4, n/4, n/4 usw., n Zahlen Es dauert insgesamt logn Zeiten, um die Sortierung abzuschließen (2^x=n, x=logn), und dann ist die Komplexität jedes Mal n. Die Zeitkomplexität ist O(n logn)
Raumkomplexität
Schlimmster Fall: n-1 rekursive Aufrufe sind erforderlich und die Raumkomplexität beträgt O(n)
Bester Fall: logn-rekursive Aufrufe sind erforderlich und die Raumkomplexität beträgt O(logn)
Stabilität des Algorithmus
Schnellsortierung ist ein instabiler Sortieralgorithmus
Zum Beispiel: Die vorhandene Sequenz ist [1, 0, 1, 3] und die Nummernauswahl „Grundlinie“. ist Die zweite 1
nach der ersten Vergleichsrunde wird zu [0, 1, 1, 3], die linke Sequenz ist [0] und die rechte Sequenz ist [1, 3] (die 1 von die richtige Reihenfolge Es ist die erste vor 1)
Es ist nicht schwer festzustellen, dass die Reihenfolge der beiden Einsen in der ursprünglichen Reihenfolge zerstört wurde und die Reihenfolge geändert wurde, was natürlich ein „ instabiler“ Sortieralgorithmus
Über O
Im vorherigen Artikel „Blasensortiermethode“ haben wir ausführlich erklärt, was O ist, daher werde ich hier nicht auf Details eingehen, sondern einfach darauf eingehen Bild
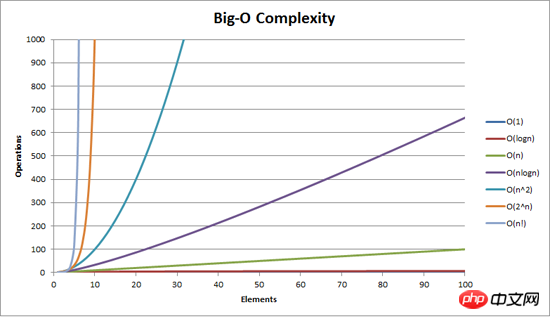
Das obige ist der detaillierte Inhalt vonSo implementieren Sie eine schnelle Sortierung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
