
Der zwanzigste und letzte Artikel in der JavaScript-Themenreihe, der den Sortierquellcode der Version 8 interpretiert
v8 ist die JavaScript-Engine von Chrome, die Informationen zu Arrays enthält Die Sortierung ist vollständig in JavaScript implementiert.
Der zum Sortieren verwendete Algorithmus hängt von der Länge des Arrays ab. Wenn die Array-Länge kleiner oder gleich 10 ist, wird die Einfügungssortierung verwendet. Wenn die Array-Länge größer als 10 ist, wird die Schnellsortierung verwendet . (Natürlich ist diese Aussage nicht streng).
Werfen wir zunächst einen Blick auf die Einfügesortierung und die Schnellsortierung.
Betrachten Sie das erste Element als geordnete Sequenz, durchlaufen Sie das Array und fügen Sie nachfolgende Elemente in die konstruierte geordnete Sequenz ein.
function insertionSort(arr) {
for (var i = 1; i < arr.length; i++) {
var element = arr[i];
for (var j = i - 1; j >= 0; j--) {
var tmp = arr[j];
var order = tmp - element;
if (order > 0) {
arr[j + 1] = tmp;
} else {
break;
}
}
arr[j + 1] = element;
}
return arr;
}
var arr = [6, 5, 4, 3, 2, 1];
console.log(insertionSort(arr));Zeitkomplexität Grad bezieht sich zum Rechenaufwand, der zur Ausführung des Algorithmus erforderlich ist. Es wird die Situation untersucht, in der sich die Größe des Eingabewerts der Unendlichkeit nähert. Im Allgemeinen ist die Anzahl der Wiederholungen der Grundoperationen im Algorithmus eine Funktion der Problemgröße n.
Der beste Fall: Das Array ist in aufsteigender Reihenfolge angeordnet, die zeitliche Komplexität beträgt: O(n)
Der schlechteste Fall: Das Array ist in absteigender Reihenfolge angeordnet, die zeitliche Komplexität beträgt: O(n²)
Stabilität bezieht sich darauf, ob dieselben Elemente nach dem Sortieren ihre relative Position beibehalten.
Es ist zu beachten, dass für instabile Sortieralgorithmen lediglich ein Beispiel zur Veranschaulichung der Instabilität angegeben werden muss, während für stabile Sortieralgorithmen der Algorithmus analysiert werden muss, um stabile Eigenschaften zu erhalten.
Zum Beispiel ist [3, 3, 1] nach der Sortierung immer noch [3, 3, 1], aber tatsächlich liegt die zweite 3 vor der ersten 3, dann handelt es sich um einen instabilen Sortieralgorithmus.
Einfügesortierung ist ein stabiler Algorithmus.
Wenn das Array sortiert werden soll oder die Problemgröße relativ klein ist, ist die Einfügungssortierung effizienter. Aus diesem Grund verwendet Version 8 die Einfügungssortierung, wenn die Array-Länge kleiner oder gleich 10 ist.
Wählen Sie ein Element als „Grundlinie“
kleiner als „Grundlinie“. " Elemente, die größer als „base“ sind, werden nach links von „base“ verschoben; Elemente, die größer als „base“ sind, werden nach rechts von „base“ verschoben.
Wiederholen Sie den ersten und zweiten Schritt für die beiden Teilmengen links und rechts der „Grundlinie“, bis in allen Teilmengen nur noch ein Element übrig bleibt.
Das Beispiel und die folgende Implementierung stammen aus „Javascript Implementation of Quicksort (Quicksort)“ von Lehrer Ruan Yifeng
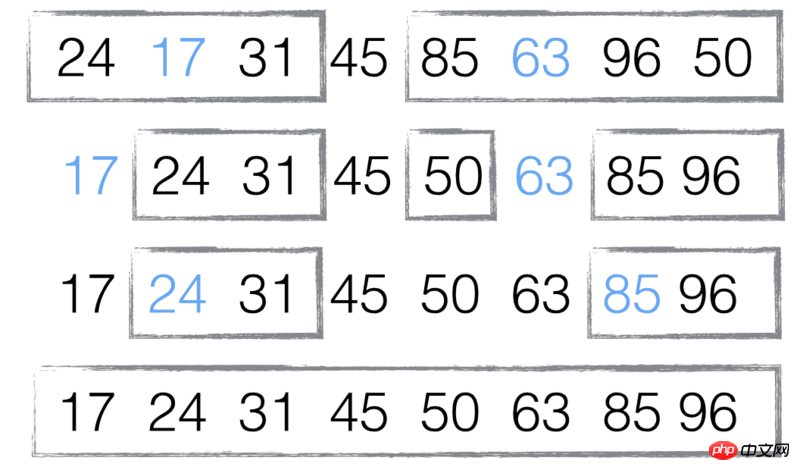
Mit Array [ 85 , 24, 63, 45, 17, 31, 96, 50] Zum Beispiel:
Wählen Sie im ersten Schritt das mittlere Element 45 als „Basis“ aus. (Der Basiswert kann beliebig gewählt werden, es ist jedoch einfacher zu verstehen, den Mittelwert zu wählen.)

Der zweite Schritt, der Reihe nach, Kombinieren Sie jedes Element mit Die „Grundlinie“ wird verglichen und bildet zwei Teilmengen, eine „weniger als 45“ und die andere „größer oder gleich 45“.

Der dritte Schritt besteht darin, den ersten und zweiten Schritt für die beiden Teilmengen zu wiederholen, bis nur noch ein Element in allen Teilmengen übrig bleibt.
var quickSort = function(arr) {
if (arr.length <= 1) { return arr; }
// 取数组的中间元素作为基准
var pivotIndex = Math.floor(arr.length / 2);
var pivot = arr.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++){
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right));
};Diese Implementierung erfordert jedoch zusätzlichen Platz zum Speichern der linken und rechten Teilmengen, daher gibt es eine andere Eine Implementierung der In-Place-Sortierung.
Werfen wir einen Blick auf das Implementierungssymbol der In-Place-Sortierung:
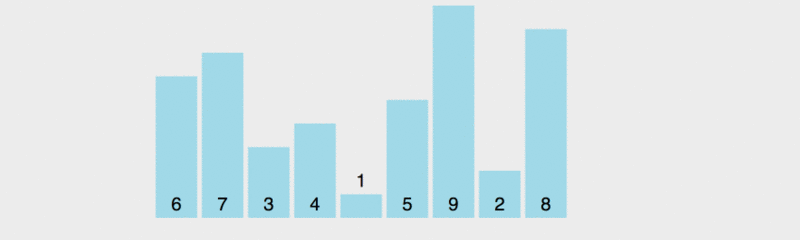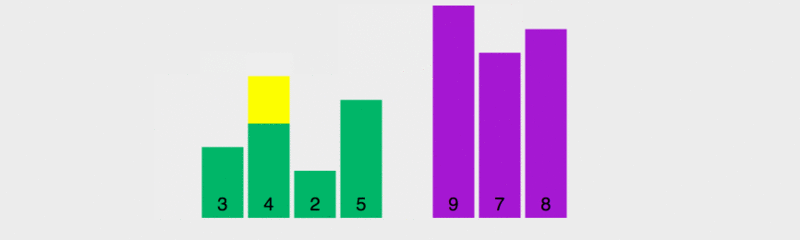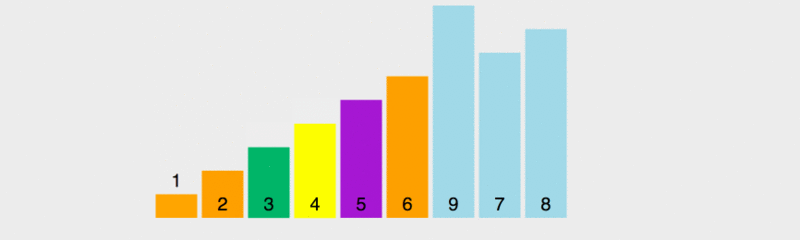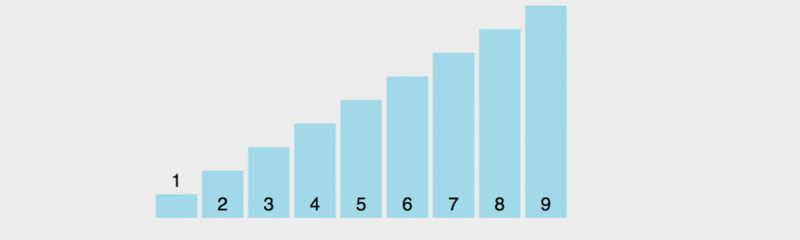
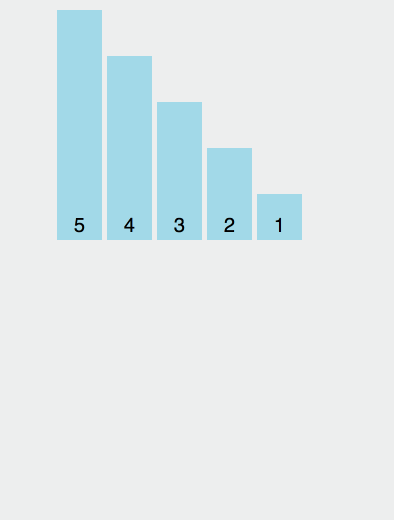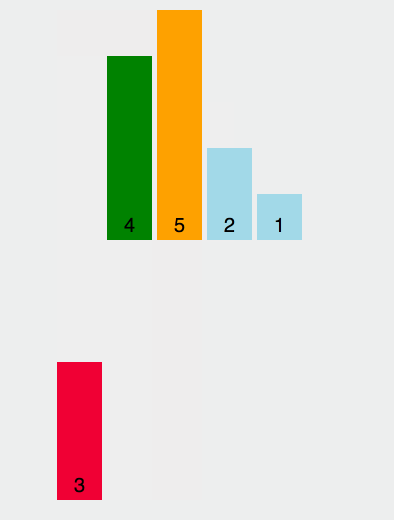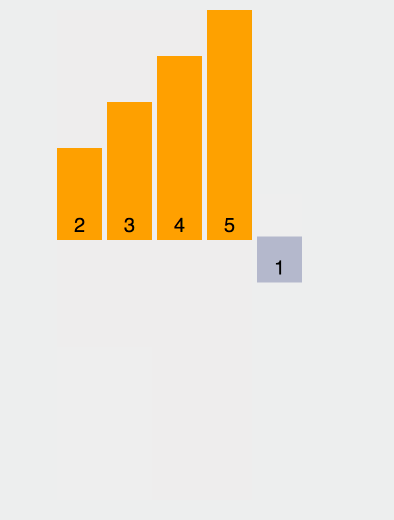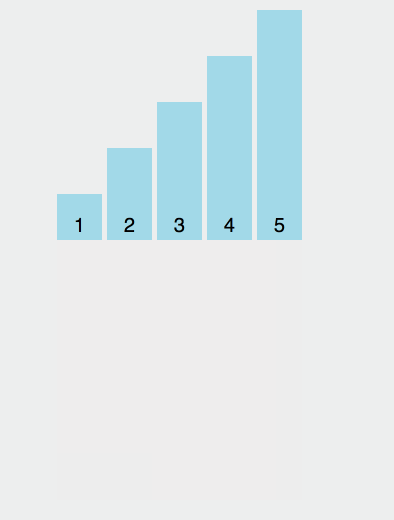
In der Reihenfolge Um es allen zu ermöglichen, das Prinzip der schnellen Sortierung zu verstehen, habe ich die Ausführungsgeschwindigkeit verlangsamt.
In diesem Diagramm besteht die Werteregel für den Benchmark darin, das Element ganz links zu verwenden. Gelb stellt den aktuellen Benchmark dar, Grün stellt Elemente dar, die kleiner als der Benchmark sind, und Lila stellt Elemente dar, die größer als der Benchmark sind.
Wir werden feststellen, dass sich das grüne Element unmittelbar rechts vom Drehpunkt befindet, das violette Element nach hinten verschoben wird und dann der Drehpunkt und das letzte grüne Element vertauscht werden. Der Pivot befindet sich an der richtigen Position, d. h. Die vorherigen Elemente sind alle kleiner als der Basiswert und die folgenden Elemente sind alle größer als der Basiswert. Nehmen Sie dann die Grundlage der vorherigen und folgenden mehreren Elemente und sortieren Sie sie.
function quickSort(arr) {
// 交换元素
function swap(arr, a, b) {
var temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
function partition(arr, left, right) {
var pivot = arr[left];
var storeIndex = left;
for (var i = left + 1; i <= right; i++) {
if (arr[i] < pivot) {
swap(arr, ++storeIndex, i);
}
}
swap(arr, left, storeIndex);
return storeIndex;
}
function sort(arr, left, right) {
if (left < right) {
var storeIndex = partition(arr, left, right);
sort(arr, left, storeIndex - 1);
sort(arr, storeIndex + 1, right);
}
}
sort(arr, 0, arr.length - 1);
return arr;
}
console.log(quickSort(6, 7, 3, 4, 1, 5, 9, 2, 8))Schnellsortierung ist eine instabile Sortierung. Wenn Sie beweisen möchten, dass eine Sortierung instabil ist, müssen Sie nur ein Beispiel nennen.
Also lasst uns eins geben~
就以数组 [1, 2, 3, 3, 4, 5] 为例,因为基准的选择不确定,假如选定了第三个元素(也就是第一个 3) 为基准,所有小于 3 的元素在前面,大于等于 3 的在后面,排序的结果没有问题。可是如果选择了第四个元素(也就是第二个 3 ),小于 3 的在基准前面,大于等于 3 的在基准后面,第一个 3 就会被移动到 第二个 3 后面,所以快速排序是不稳定的排序。
阮一峰老师的实现中,基准取的是中间元素,而原地排序中基准取最左边的元素。快速排序的关键点就在于基准的选择,选取不同的基准时,会有不同性能表现。
快速排序的时间复杂度最好为 O(nlogn),可是为什么是 nlogn 呢?来一个并不严谨的证明:
在最佳情况下,每一次都平分整个数组。假设数组有 n 个元素,其递归的深度就为 log2n + 1,时间复杂度为 O(n)[(log2n + 1)],因为时间复杂度考察当输入值大小趋近无穷时的情况,所以会忽略低阶项,时间复杂度为:o(nlog2n)。
如果一个程序的运行时间是对数级的,则随着 n 的增大程序会渐渐慢下来。如果底数是 10,lg1000 等于 3,如果 n 为 1000000,lgn 等于 6,仅为之前的两倍。如果底数为 2,log21000 的值约为 10,log21000000 的值约为 19,约为之前的两倍。我们可以发现任意底数的一个对数函数其实都相差一个常数倍而已。所以我们认为 O(logn)已经可以表达所有底数的对数了,所以时间复杂度最后为: O(nlogn)。
而在最差情况下,如果对一个已经排序好的数组,每次选择基准元素时总是选择第一个元素或者最后一个元素,那么每次都会有一个子集是空的,递归的层数将达到 n,最后导致算法的时间复杂度退化为 O(n²)。
这也充分说明了一个基准的选择是多么的重要,而 v8 为了提高性能,就对基准的选择做了很多优化。
v8 选择基准的原理是从头和尾之外再选择一个元素,然后三个值排序取中间值。
当数组长度大于 10 但是小于 1000 的时候,取中间位置的元素,实现代码为:
// 基准的下标 // >> 1 相当于除以 2 (忽略余数) third_index = from + ((to - from) >> 1);
当数组长度大于 1000 的时候,每隔 200 ~ 215 个元素取一个值,然后将这些值进行排序,取中间值的下标,实现的代码为:
// 简单处理过
function GetThirdIndex(a, from, to) {
var t_array = new Array();
// & 位运算符
var increment = 200 + ((to - from) & 15);
var j = 0;
from += 1;
to -= 1;
for (var i = from; i < to; i += increment) {
t_array[j] = [i, a[i]];
j++;
}
// 对随机挑选的这些值进行排序
t_array.sort(function(a, b) {
return comparefn(a[1], b[1]);
});
// 取中间值的下标
var third_index = t_array[t_array.length >> 1][0];
return third_index;
}也许你会好奇 200 + ((to - from) & 15) 是什么意思?
& 表示是按位与,对整数操作数逐位执行布尔与操作。只有两个操作数中相对应的位都是 1,结果中的这一位才是 1。
以 15 & 127 为例:
15 二进制为: (0000 1111)
127 二进制为:(1111 1111)
按位与结果为:(0000 1111)= 15
所以 15 & 127 的结果为 15。
注意 15 的二进制为: 1111,这就意味着任何和 15 按位与的结果都会小于或者等于 15,这才实现了每隔 200 ~ 215 个元素取一个值。
终于到了看源码的时刻!源码地址为:https://github.com/v8/v8/blob/master/src/js/array.js#L758。
function InsertionSort(a, from, to) {
for (var i = from + 1; i < to; i++) {
var element = a[i];
for (var j = i - 1; j >= from; j--) {
var tmp = a[j];
var order = comparefn(tmp, element);
if (order > 0) {
a[j + 1] = tmp;
} else {
break;
}
}
a[j + 1] = element;
}
};
function QuickSort(a, from, to) {
var third_index = 0;
while (true) {
// Insertion sort is faster for short arrays.
if (to - from <= 10) {
InsertionSort(a, from, to);
return;
}
if (to - from > 1000) {
third_index = GetThirdIndex(a, from, to);
} else {
third_index = from + ((to - from) >> 1);
}
// Find a pivot as the median of first, last and middle element.
var v0 = a[from];
var v1 = a[to - 1];
var v2 = a[third_index];
var c01 = comparefn(v0, v1);
if (c01 > 0) {
// v1 < v0, so swap them.
var tmp = v0;
v0 = v1;
v1 = tmp;
} // v0 <= v1.
var c02 = comparefn(v0, v2);
if (c02 >= 0) {
// v2 <= v0 <= v1.
var tmp = v0;
v0 = v2;
v2 = v1;
v1 = tmp;
} else {
// v0 <= v1 && v0 < v2
var c12 = comparefn(v1, v2);
if (c12 > 0) {
// v0 <= v2 < v1
var tmp = v1;
v1 = v2;
v2 = tmp;
}
}
// v0 <= v1 <= v2
a[from] = v0;
a[to - 1] = v2;
var pivot = v1;
var low_end = from + 1; // Upper bound of elements lower than pivot.
var high_start = to - 1; // Lower bound of elements greater than pivot.
a[third_index] = a[low_end];
a[low_end] = pivot;
// From low_end to i are elements equal to pivot.
// From i to high_start are elements that haven&#39;t been compared yet.
partition: for (var i = low_end + 1; i < high_start; i++) {
var element = a[i];
var order = comparefn(element, pivot);
if (order < 0) {
a[i] = a[low_end];
a[low_end] = element;
low_end++;
} else if (order > 0) {
do {
high_start--;
if (high_start == i) break partition;
var top_elem = a[high_start];
order = comparefn(top_elem, pivot);
} while (order > 0);
a[i] = a[high_start];
a[high_start] = element;
if (order < 0) {
element = a[i];
a[i] = a[low_end];
a[low_end] = element;
low_end++;
}
}
}
if (to - high_start < low_end - from) {
QuickSort(a, high_start, to);
to = low_end;
} else {
QuickSort(a, from, low_end);
from = high_start;
}
}
}
var arr = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0];
function comparefn(a, b) {
return a - b
}
QuickSort(arr, 0, arr.length)
console.log(arr)我们以数组 [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0] 为例,分析执行的过程。
1.执行 QuickSort 函数 参数 from 值为 0,参数 to 的值 11。
2.10 < to - from < 1000 第三个基准元素的下标为 (0 + 11 >> 1) = 5,基准值 a[5] 为 5。
3.比较 a[0] a[10] a[5] 的值,然后根据比较结果修改数组,数组此时为 [0, 9, 8, 7, 6, 5, 4, 3, 2, 1, 10]
4.将基准值和数组的第(from + 1)个即数组的第二个元素互换,此时数组为 [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10],此时在基准值 5 前面的元素肯定是小于 5 的,因为第三步已经做了一次比较。后面的元素是未排序的。
我们接下来要做的就是把后面的元素中小于 5 的全部移到 5 的前面。
5.然后我们进入 partition 循环,我们依然以这个数组为例,单独抽出来写个 demo 讲一讲
// 假设代码执行到这里,为了方便演示,我们直接设置 low_end 等变量的值
// 可以直接复制到浏览器中查看数组变换效果
var a = [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10]
var low_end = 1;
var high_start = 10;
var pivot = 5;
console.log(&#39;起始数组为&#39;, a)
partition: for (var i = low_end + 1; i < high_start; i++) {
var element = a[i];
console.log(&#39;循环当前的元素为:&#39;, a[i])
var order = element - pivot;
if (order < 0) {
a[i] = a[low_end];
a[low_end] = element;
low_end++;
console.log(a)
}
else if (order > 0) {
do {
high_start--;
if (high_start == i) break partition;
var top_elem = a[high_start];
order = top_elem - pivot;
} while (order > 0);
a[i] = a[high_start];
a[high_start] = element;
console.log(a)
if (order < 0) {
element = a[i];
a[i] = a[low_end];
a[low_end] = element;
low_end++;
}
console.log(a)
}
}
console.log(&#39;最后的结果为&#39;, a)
console.log(low_end)
console.log(high_start)6.此时数组为 [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10],循环从第三个元素开始,a[i] 的值为 8,因为大于基准值 5,即 order > 0,开始执行 do while 循环,do while 循环的目的在于倒序查找元素,找到第一个小于基准值的元素,然后让这个元素跟 a[i] 的位置交换。
第一个小于基准值的元素为 1,然后 1 与 8 交换,数组变成 [0, 5, 1, 7, 6, 9, 4, 3, 2, 8, 10]。high_start 的值是为了记录倒序查找到哪里了。
7. Zu diesem Zeitpunkt wird der Wert von a[i] 1 und dann 1 mit dem Basiswert 5 ausgetauscht. Das Array wird zu [0, 1, 5, 7, 6, 9, 4, 3, 2, 8, 10] und der Wert von low_end wird um 1 erhöht. Der Wert von low_end besteht darin, den Basiswert aufzuzeichnen.
8. Die Schleife wird dann ausgeführt und durchläuft das vierte Element 7, was mit den Schritten 6 und 7 übereinstimmt. Das Array wird zuerst zu [0, 1, 5, 2, 6, 9, 4, 3, 7, 8, 10] und dann zu [0, 1, 2, 5, 6, 9, 4, 3, 7, 8, 10]
9 . Durchlaufen Sie das fünfte Element 6, genau wie in den Schritten 6 und 7. Das Array wird zuerst zu [0, 1, 2, 5, 3, 9, 4, 6, 7, 8, 10] und dann zu [0, 1, 2, 3, 5, 9, 4, 6, 7, 8, 10]
10. Durchlaufen Sie das sechste Element 9 und befolgen Sie die Schritte 6 und 7. Die Schritte Sind gleich, wird das Array zuerst zu [0, 1, 2, 3, 5, 4, 9, 6, 7, 8, 10] und dann zu [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10]
11. Da i == high_start bedeutet, dass die Vorwärts- und Rückwärtssuche schließlich zusammen gefunden wird. Die folgenden Elemente sind definitiv größer als der Basiswert. Verlassen Sie die Schleife
12. Das Ergebnis nach dem Durchlaufen ist [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10]. Die Elemente vor dem Basiswert 5 sind alle kleiner als 5. und die folgenden Elemente sind alle größer als 5. Dann führen wir QuickSort
13 für die beiden Teilmengen durch. Zu diesem Zeitpunkt ist der Low_End-Wert 5, der High_Start-Wert 6 und der Wert von to immer noch 10 , der Wert von from ist immer noch 0 und das Ergebnis von to - high_start < low_end - from ist true, wir sortieren QuickSort(a, 6, 10), also die folgenden Elemente, aber beachten Sie, dass im neuen QuickSort, weil die Wenn der Wert von „von – bis“ kleiner als 10 ist, wird diesmal tatsächlich die Einfügungssortierung verwendet. Um genau zu sein: Wenn die Array-Länge größer als 10 ist, verwendet v8 eine hybride Sortiermethode aus Schnellsortierung und Einfügungssortierung.
14. Dann wird to = low_end auf 5 gesetzt. Aufgrund von while(true) wird es erneut ausgeführt. Der Wert von to - from ist 5 und InsertionSort(a, 0, 5 ausgeführt), d. h. eine Einfügungssortierung für das Element vor dem Referenzwert durchführen.
15. Da es in der Beurteilung von to - from <= 10 eine Return-Anweisung gibt, endet die while-Schleife.
16.v8 Nachdem Sie eine schnelle Sortierung für das Array durchgeführt haben, dann eine Einfügungssortierung für die beiden Teilmengen durchgeführt und schließlich das Array in ein korrekt sortiertes Array geändert haben.
Schließlich nehmen wir ein schematisches Diagramm, um die Einfügungssortierung und die schnelle Sortierung zu erleben:

Das Das Bild stammt von https://www.toptal.com/developers/sorting-algorithms
JavaScript Special Series-Verzeichnisadresse: https://github.com/mqyqingfeng/Blog.
Die JavaScript-Themenreihe wird voraussichtlich etwa zwanzig Artikel umfassen und sich hauptsächlich mit der Implementierung einiger Funktionspunkte in der täglichen Entwicklung befassen, z. B. Anti-Shake, Drosselung, Deduplizierung, Typbeurteilung, Kopieren, Maximalwert, Abflachung, Curry, Rekursion, Neuordnung, Sortierung usw. zeichnen sich durch das Studium (Chao) der Implementierung von Unterstrichen und jQuery aus.
![]()
Das obige ist der detaillierte Inhalt vonProbleme mit der Sortierung des Quellcodes der Version 8 in JavaScript. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




