Dynamische Programmierbeispielanalyse von erweiterten JavaScript-Algorithmen

Tatsächlich werden in unserer Front-End-Entwicklung nicht viele fortgeschrittene Algorithmen verwendet. In den meisten Fällen können if-Anweisungen, for-Anweisungen, switch-Anweisungen usw. gelöst werden. Wenn es etwas komplizierter ist, könnten Sie darüber nachdenken, es mithilfe der Rekursion zu lösen. In diesem Artikel wird hauptsächlich die dynamische Programmierung fortgeschrittener JavaScript-Programmieralgorithmen vorgestellt und die Prinzipien, Implementierungstechniken und zugehörigen Verwendungsvorkehrungen des dynamischen JavaScript-Programmieralgorithmus anhand von Beispielen analysiert.

Es sollte jedoch beachtet werden, dass die Rekursion einfach zu schreiben ist, die tatsächliche Ausführungseffizienz jedoch nicht hoch ist.

Schauen wir uns noch einmal den dynamischen Programmieralgorithmus an:

Die dynamische Programmierlösung beginnt von unten, um das Problem zu lösen, löst alle kleinen Probleme und führt sie dann zu einer Gesamtlösung zusammen, um das Problem zu lösen ganzes Problem. Großes Problem.

Beispiel (Berechnung der Fibonacci-Folge)

Fibonacci-Folge bezieht sich auf eine Folge von 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 , 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368...

Diese Sequenz beginnt mit dem 3. Element. Anfangs ist jeder Term gleich der Summe des vorherigen zwei Begriffe.

Für diese Sequenz kann eine rekursive Funktion verwendet werden, um den n-ten Wert zu berechnen

// 斐波那契数列
function recurFib(n) {
    if(n < 2){
      return n ;
    }else {
//          document.write("第"+(n-1)+"次计算 n-1="+(n-1)+recurFib(n-1)+&#39;   &#39;);
//          document.write("n-2="+(n-2)+recurFib(n-2)+"<br>");
      return recurFib(n-1)+recurFib(n-2)
    }
}

Indeed It ist ein sehr prägnanter Code, der verwendet wird, um auszudrücken, wie oft die Funktion ausgeführt werden muss, wenn n = ist. Eine anspruchsvolle Person kann jedoch auf einen Blick erkennen, dass mit zunehmendem n auch die Anzahl der Ausführungen zunimmt sehr groß sein.

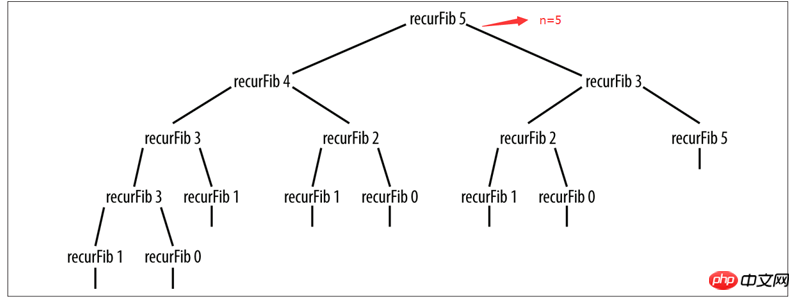
Wenn n=5, ist der Rekursionsbaum sehr groß geworden... Es kann vorhergesagt werden, dass, wenn n=10 oder sogar n=100...

Um den Unterschied in der Ausführungseffizienz rekursiver Funktionen zu verstehen, schauen wir uns an, wie dynamische Programmierung durchgeführt wird

function dynFib(n) {
  let val = [];
  for(let i = 0; i <= n; ++i){
    val[i]=0;
  }
  if(n ===1 || n === 2){
    return 1;
  }
  else {
    val[1] =1;
    val[2] = 2;
    for(let i = 3; i <= n; ++i){
      val[i] = val [i-1] +val[i-2] ;
    }
  }
  return val[n-1]
}

Bestanden Das Zwischenergebnis wird im Array val gespeichert. Wenn die zu berechnende Fibonacci-Zahl 1 oder 2 ist, dann gibt die if-Anweisung 1 zurück. Andernfalls werden die Werte 1 und 2 an den Positionen 1 und 2 im Val-Array gespeichert.

Die Schleife durchläuft von 3 zu den Eingabeparametern und weist jedes Element des Arrays der Summe der ersten beiden Elemente zu. Die Schleife endet und der letzte Elementwert des Arrays ist der endgültig berechnete Fibonacci-Wert Wert, dieser Wert wird auch als Rückgabewert der Funktion verwendet.

Als nächstes können Sie eine einfache Testfunktion schreiben, um die Laufzeit der beiden zu vergleichen.

// 定义一个测试函数，将待测函数作为参数传入
function test(func,n){
  let start = new Date().getTime();//起始时间
  let res = func(n);//执行待测函数
  document.write(&#39;<br>&#39;+&#39;当n=&#39;+n+&#39;的时候 &#39;+res+&#39;<br>&#39;);
  let end = new Date().getTime();//结束时间
  return (end - start)+"ms";//返回函数执行需要时间
}

Funktionsausführung drucken

let time = test(recurFib,40);
document.write(time);
let time2 = test(dynFib,40);
document.write(time2);

Die Ergebnisse sind wie folgt:

Schließlich haben Sie vielleicht erkannt, dass Sie bei der Berechnung der Fibonacci-Folge mithilfe eines iterativen Schemas darauf verzichten können unter Verwendung eines Arrays von.

Der Grund, warum Arrays benötigt werden, liegt darin, dass dynamische Programmieralgorithmen normalerweise Zwischenergebnisse speichern müssen.

Das Folgende ist die iterative Version der Fibonacci-Funktionsdefinition

function iterFib(n) {
  let last = 1;
  let nextLast = 1;
  let result = 1;
  for (let i = 2; i < n; ++i) {
    result = last + nextLast;
    nextLast = last;
    last = result;
  }
  return result;
}

Natürlich ist diese iterative Version Das Gleiche wie Die Array-Version ist ebenso effizient.

Verwandte Empfehlungen:

Dynamische Programmierung des PHP-Algorithmus-Lernens

PHP-Algorithmus-Lernen, dynamische Programmierung (2)

Detaillierte Erläuterung des Änderungsproblems der dynamischen Programmierung

Das obige ist der detaillierte Inhalt vonDynamische Programmierbeispielanalyse von erweiterten JavaScript-Algorithmen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!