Künstliches neuronales Netzwerk ist ein algorithmisches mathematisches Modell, das die Verhaltensmerkmale tierischer neuronaler Netzwerke nachahmt und eine verteilte parallele Informationsverarbeitung durchführt. Diese Art von Netzwerk ist auf die Komplexität des Systems angewiesen, um den Zweck der Informationsverarbeitung durch Anpassen der miteinander verbundenen Beziehungen zwischen einer großen Anzahl interner Knoten zu erreichen, und verfügt über die Fähigkeit zum Selbstlernen und Anpassen. Dieser Artikel stellt hauptsächlich die theoretischen Grundlagen des neuronalen Netzwerks und die detaillierte Erklärung der Python-Implementierung vor. Ich hoffe, dass er jedem helfen kann.
1. Mehrschichtiges vorwärtsgerichtetes neuronales Netzwerk
Mehrschichtiges vorwärtsgerichtetes neuronales Netzwerk besteht aus drei Teilen: Ausgabeschicht, verborgene Schicht, Ausgabe Schicht, jede Schicht besteht aus Einheiten;
Die Eingabeschicht wird vom Instanzmerkmalsvektor des Trainingssatzes übergeben und über das Gewicht des Verbindungsknotens an die nächste Schicht übergeben Die Ebene ist die Eingabe der nächsten Ebene. Die Anzahl der ausgeblendeten Ebenen ist beliebig, es gibt nur eine Eingabeebene und nur eine Ausgabeebene. Mit Ausnahme der Eingabeebene beträgt die Summe der ausgeblendeten Ebenen Schichten und Ausgabeschichten sind n, dann wird das neuronale Netzwerk als n-schichtiges neuronales Netzwerk bezeichnet. Die folgende Abbildung zeigt eine gewichtete Summierung in einer Schicht, transformiert und ausgegeben Gleichungen; Theoretisch kann der Trainingssatz jede beliebige Gleichung simulieren, wenn genügend verborgene Schichten vorhanden sind
Verwendung Vor der Verwendung eines neuronalen Netzwerks ist es notwendig, die Anzahl der Schichten des neuronalen Netzwerks und die Anzahl der Einheiten in jeder Schicht zu bestimmen
Um Um den Lernprozess zu beschleunigen, muss der Merkmalsvektor normalerweise auf einen Wert zwischen 0 und 1 standardisiert werden, bevor er an die Eingabeebene übergeben wird.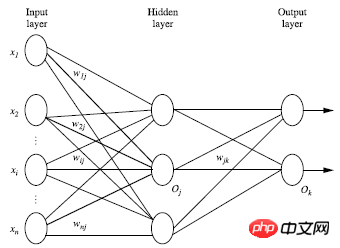 
Zum Beispiel: Eigenwert A kann drei Werte haben (a0, a1, a2), Dann können 3 Eingabeeinheiten verwendet werden, um A darzustellenWenn A=a0 , der Einheitswert, der a0 darstellt, ist 1, und der Rest ist 0; Wenn A=a1, ist der Einheitswert, der a1 darstellt, 1, der Rest ist 0; 1 und der Rest ist 0;
Neuronales Netzwerk löst nicht nur das Klassifizierungsproblem, sondern kann auch Regressionsprobleme lösen. Bei Klassifizierungsproblemen kann bei zwei Kategorien jeweils eine Ausgabeeinheit (0 und 1) zur Darstellung der beiden Kategorien verwendet werden. Bei mehr als zwei Kategorien wird jede Kategorie durch eine Ausgabeeinheit, also die Anzahl der Einheiten, dargestellt in der Ausgabeebene entspricht normalerweise einer Kategoriemenge. Es gibt keine klaren Regeln für die Gestaltung der optimalen Anzahl verborgener Schichten. Experimente werden im Allgemeinen auf der Grundlage experimenteller Testfehler und Genauigkeit verbessert.
3. Kreuzvalidierungsmethode
Wie berechnet man die Genauigkeit? Die einfachste Methode besteht darin, einen Satz von Trainingssätzen und Testsätzen zu verwenden. Der Trainingssatz wird in das Modell eingegeben, um die Testergebnisse zu erhalten Testsatz, um die Genauigkeit zu ermitteln.
Eine häufig verwendete Methode im Bereich des maschinellen Lernens ist die Kreuzvalidierungsmethode. Ein Datensatz wird nicht in 2 Teile unterteilt, sondern kann in 10 Teile unterteilt werden.
Das erste Mal: Der 1. Teil wird als Testsatz verwendet und die restlichen 9 Teile werden als Trainingssatz verwendet ;
Das 2. Mal: Der 2. Teil wird als Testsatzsatz verwendet und die restlichen 9 Sätze werden als Trainingssätze verwendetNach 10 Trainingseinheiten 10 Sätze Es werden die Genauigkeitsgrade ermittelt und die durchschnittliche Genauigkeit dieser 10 Datensätze ermittelt. Hier ist 10 ein Sonderfall. Im Allgemeinen werden die Daten in k Teile unterteilt, und der Algorithmus wird als K-fache Kreuzvalidierung bezeichnet. Das heißt, einer der k Teile wird jedes Mal als Testsatz ausgewählt und die verbleibenden k-1 Teile werden als verwendet Das k-malige Wiederholen des Trainingssatzes ist eine wissenschaftlichere und genauere Methode.
4. BP-Algorithmus
Verarbeiten Sie Instanzen im Trainingssatz durch Iteration; 🎜>Vergleichen Sie die Differenz zwischen dem vorhergesagten Wert und dem wahren Wert nach dem Durchlaufen des neuronalen Netzwerks
Gewichte und Vorspannungen initialisieren: Zufällig zwischen -1 und 1 (oder anders) initialisieren, jede Einheit hat eine Vorspannung für jede Trainingsinstanz X, führen Sie die folgenden Schritte aus:
1 Schichtvorwärtsübertragung: 
Von der Eingabeschicht zur verborgenen Schicht:
Von der verborgenen Ebene zur Ausgabeebene:
Wenn wir die beiden Formeln zusammenfassen, erhalten wir:
Ij ist der Einheitswert der aktuellen Ebene und Oi ist der Einheit des vorherigen Schichtwerts, wij ist der Gewichtungswert, der die beiden Einheitswerte zwischen den beiden Schichten verbindet, und sitaj ist der Bias-Wert jeder Schicht. Wir müssen eine nichtlineare Transformation für die Ausgabe jeder Ebene durchführen. Das schematische Diagramm sieht wie folgt aus:
Die Ausgabe der aktuellen Ebene ist Ij und f ist die nichtlineare Transformation Funktion, auch Aktivierungsfunktion genannt, definiert wie folgt:
Das heißt, die Ausgabe jeder Ebene ist:
Auf diese Weise kann der Eingabewert weitergeleitet werden. Erhalten Sie den Ausgabewert jeder Ebene.
2. Umgekehrte Ausbreitung entsprechend dem Fehler: wobei Tk der wahre Wert und Ok der vorhergesagte Wert ist
Für den verborgenen Ebene:
Gewichtsaktualisierung: wobei l die Lernrate ist
Bias-Aktualisierung:
3. Abbruchbedingungen
Die voreingenommene Aktualisierung liegt unter einem bestimmten Schwellenwert.
Die vorhergesagte Fehlerrate liegt unter einem bestimmten Schwellenwert Zyklen werden erreicht;
tanh(x)=sinh(x)/cosh(x)
sinh(x)=(exp(x)-exp(-x))/2
cosh(x)=( exp( x)+exp(-x))/2
5. Python-Implementierung von BP-Neuronales Netzwerk
Sie müssen zuerst das Numpy-Modul importierenimport numpy as np
def tanh(x): return np.tanh(x) def tanh_deriv(x): return 1.0 - np.tanh(x)*np.tanh(x) def logistic(x): return 1/(1 + np.exp(-x)) def logistic_derivative(x): return logistic(x)*(1-logistic(x))
class NeuralNetwork:
def __init__(self, layers, activation='tanh'):
"""
:param layers: A list containing the number of units in each layer.
Should be at least two values
:param activation: The activation function to be used. Can be
"logistic" or "tanh"
"""
if activation == 'logistic':
self.activation = logistic
self.activation_deriv = logistic_derivative
elif activation == 'tanh':
self.activation = tanh
self.activation_deriv = tanh_deriv
self.weights = []
for i in range(1, len(layers) - 1):
self.weights.append((2*np.random.random((layers[i - 1] + 1, layers[i] + 1))-1)*0.25)
self.weights.append((2*np.random.random((layers[i] + 1, layers[i + 1]))-1)*0.25)
def fit(self, X, y, learning_rate=0.2, epochs=10000):
X = np.atleast_2d(X)
temp = np.ones([X.shape[0], X.shape[1]+1])
temp[:, 0:-1] = X
X = temp
y = np.array(y)
for k in range(epochs):
i = np.random.randint(X.shape[0])
a = [X[i]]
for l in range(len(self.weights)):
a.append(self.activation(np.dot(a[l], self.weights[l])))
error = y[i] - a[-1]
deltas = [error * self.activation_deriv(a[-1])]
for l in range(len(a) - 2, 0, -1):
deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))
deltas.reverse()
for i in range(len(self.weights)):
layer = np.atleast_2d(a[i])
delta = np.atleast_2d(deltas[i])
self.weights[i] += learning_rate * layer.T.dot(delta)
def predict(self, x):
x = np.array(x)
temp = np.ones(x.shape[0]+1)
temp[0:-1] = x
a = temp
for l in range(0, len(self.weights)):
a = self.activation(np.dot(a, self.weights[l]))
return afrom BP import NeuralNetwork import numpy as np nn = NeuralNetwork([2,2,1], 'tanh') x = np.array([[0,0], [0,1], [1,0], [1,1]]) y = np.array([1,0,0,1]) nn.fit(x,y,0.1,10000) for i in [[0,0], [0,1], [1,0], [1,1]]: print(i, nn.predict(i))
([0, 0], array([ 0.99738862])) ([0, 1], array([ 0.00091329])) ([1, 0], array([ 0.00086846])) ([1, 1], array([ 0.99751259]))
Über Numpy zur flexiblen Definition Neuronale Netze in Python Beispiele für Strukturen
Teilen einfacher Beispiele für die Implementierung rekursiver neuronaler Netze in Python
Detaillierte Grafik- und Texterklärung eines einfachen neuronalen Netzes In JavaScript implementierter Algorithmus
Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung der theoretischen Grundlagen des neuronalen Netzwerks und der Python-Implementierungsmethode. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
