Detaillierte Erläuterung des PHP-Sortieralgorithmus Heap-Sortierung

Dieser Artikel stellt hauptsächlich den in PHP implementierten Heap-Sortieralgorithmus vor. Er hat einen gewissen Referenzwert. Ich hoffe, er kann jedem helfen.

Einführung in den Algorithmus:

Hier zitiere ich direkt den Anfang von „Dahua Data Structure“:

Wie bereits erwähnt, ist die einfache Auswahlsortierung das Auswählen Der kleinste Datensatz unter den n zu sortierenden Datensätzen erfordert n - 1 Vergleiche. Das ist verständlich. Es ist normal, dass man die ersten Daten so oft findet, wie man sonst wissen kann, dass es sich um den kleinsten Datensatz handelt.

Leider speichert dieser Vorgang nicht die Vergleichsergebnisse der letzten Fahrt. Viele Vergleiche wurden bei der vorherigen Fahrt durchgeführt, aber aufgrund der vorherigen Fahrt waren diese Vergleichsergebnisse Da die Werte beim Sortieren nicht gespeichert wurden, wurden diese Vergleichsvorgänge beim nächsten Sortierdurchgang wiederholt, sodass eine größere Anzahl von Vergleichen aufgezeichnet wurde.

Wenn Sie jedes Mal den kleinsten Datensatz auswählen und basierend auf den Vergleichsergebnissen entsprechende Anpassungen an anderen Datensätzen vornehmen können, ist die Gesamteffizienz der Sortierung sehr hoch. Die Heap-Sortierung ist eine Verbesserung gegenüber der einfachen Auswahlsortierung, und die Auswirkung dieser Verbesserung ist sehr offensichtlich.

Grundidee:

Bevor wir die Heap-Sortierung einführen, stellen wir zunächst den Heap vor:

Die Definition in „Dahua Data Structure“: Heap Es ist ein vollständiger Binärbaum mit den folgenden Eigenschaften: Der Wert jedes Knotens ist größer oder gleich dem Wert seines linken und rechten untergeordneten Knotens und wird zu einem Big-Top-Heap (großer Root-Heap); oder der Wert jedes Knotens ist kleiner als oder gleich dem Wert seiner linken und rechten Knoten und wird zum kleinen oberen Stapel (kleiner Wurzelstapel).

Als ich das sah, hatte ich auch Zweifel, ob der Heap ein vollständiger Binärbaum ist. Es gibt auch Leute im Internet, die sagen, dass es sich nicht um einen vollständigen Binärbaum handelt, aber egal, ob der Heap Da es sich um einen vollständigen Binärbaum handelt, behalte ich mir meine Meinung vor. Wir müssen nur wissen, dass wir hier einen großen Root-Heap (kleinen Root-Heap) in Form eines vollständigen Binärbaums verwenden, hauptsächlich um die Speicherung und Berechnung zu erleichtern (wir werden die Bequemlichkeit später sehen).

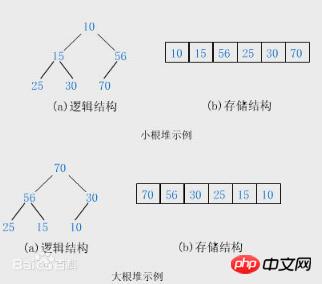
Heap-Sortieralgorithmus:

Heap-Sortierung ist eine Sortiermethode mithilfe eines Heaps (vorausgesetzt, es handelt sich um einen großen Root-Heap). Die Grundidee besteht darin, die zu sortierende Sequenz in einen großen Root-Heap zu konstruieren. Zu diesem Zeitpunkt ist der Maximalwert der gesamten Sequenz der Wurzelknoten oben im Heap. Entfernen Sie es (tauschen Sie es tatsächlich mit dem letzten Element des Heap-Arrays aus, wobei das letzte Element den Maximalwert hat) und rekonstruieren Sie dann die verbleibenden n-1 Sequenzen in einem Heap, sodass Sie die n Elemente erhalten Der nächstkleinere Wert. Wenn Sie dies wiederholt ausführen, können Sie eine geordnete Reihenfolge erhalten.

Grundoperationen des großen Root-Heap-Sortieralgorithmus:

① Beim Erstellen eines Heaps wird der Heap ständig angepasst, beginnend bei len/2 und bis zum erster Knoten, hier ist len ​​die Anzahl der Elemente im Heap. Der Prozess zum Erstellen eines Heaps ist ein linearer Prozess. Der Prozess zum Anpassen des Heaps wird immer von len/2 auf 0 aufgerufen, was o(h1) + o(h2) ... + o(hlen/2) entspricht. wobei h die Tiefe des Knotens darstellt, len /2 die Anzahl der Knoten darstellt. Dies ist ein Summierungsprozess und das Ergebnis ist linear O(n).

②Anpassungsheap: Der Anpassungsheap wird beim Aufbau des Heaps und auch beim Heap-Sortierungsprozess verwendet. Die Idee besteht darin, Knoten i mit seinen untergeordneten Knoten links (i) und rechts (i) zu vergleichen und den größten (oder kleinsten) der drei auszuwählen, wenn der größte (kleinste) Wert nicht Knoten i, sondern einer seiner untergeordneten Knoten ist Dort interagiert der Knoten i mit dem Knoten, und dann wird der Heap-Anpassungsprozess aufgerufen. Dies ist ein rekursiver Prozess. Die zeitliche Komplexität des Prozesses zum Anpassen des Heaps hängt von der Tiefe des Heaps ab. Es handelt sich um einen Vorgang von lgn, da er entlang der Tiefenrichtung angepasst wird.

③Heap-Sortierung: Die Heap-Sortierung wird mithilfe der beiden oben genannten Prozesse durchgeführt. Die erste besteht darin, einen Heap basierend auf Elementen zu erstellen. Nehmen Sie dann den Wurzelknoten des Heaps heraus (normalerweise tauschen Sie ihn gegen den letzten Knoten aus), setzen Sie den Heap-Anpassungsprozess mit den ersten Len-1-Knoten fort und nehmen Sie dann den Wurzelknoten heraus, bis alle Knoten entfernt wurden. Die zeitliche Komplexität des Heap-Sortierprozesses beträgt O(nlgn). Da die Zeitkomplexität beim Erstellen eines Heaps O (n) beträgt (ein Aufruf); die Zeitkomplexität beim Anpassen des Heaps beträgt lgn und wird n-1-mal aufgerufen, sodass die Zeitkomplexität der Heap-Sortierung O (nlgn) beträgt.

Dieser Prozess erfordert viele Diagramme, um ihn klar zu verstehen, aber ich bin faul. . . . . .

Algorithmusimplementierung:

<?php

//堆排序（对简单选择排序的改进）

function swap(array &$arr,$a,$b){
 $temp = $arr[$a];
 $arr[$a] = $arr[$b];
 $arr[$b] = $temp;
}

//调整 $arr[$start]的关键字，使$arr[$start]、$arr[$start+1]、、、$arr[$end]成为一个大根堆（根节点最大的完全二叉树）
//注意这里节点 s 的左右孩子是 2*s + 1 和 2*s+2 （数组开始下标为 0 时）
function HeapAdjust(array &$arr,$start,$end){
 $temp = $arr[$start];
 //沿关键字较大的孩子节点向下筛选
 //左右孩子计算（我这里数组开始下标识 0）
 //左孩子2 * $start + 1，右孩子2 * $start + 2
 for($j = 2 * $start + 1;$j <= $end;$j = 2 * $j + 1){
  if($j != $end && $arr[$j] < $arr[$j + 1]){
   $j ++; //转化为右孩子
  }
  if($temp >= $arr[$j]){
   break; //已经满足大根堆
  }
  //将根节点设置为子节点的较大值
  $arr[$start] = $arr[$j];
  //继续往下
  $start = $j;
 }
 $arr[$start] = $temp;
}

function HeapSort(array &$arr){
 $count = count($arr);
 //先将数组构造成大根堆（由于是完全二叉树，所以这里用floor($count/2)-1，下标小于或等于这数的节点都是有孩子的节点)
 for($i = floor($count / 2) - 1;$i >= 0;$i --){
  HeapAdjust($arr,$i,$count);
 }
 for($i = $count - 1;$i >= 0;$i --){
  //将堆顶元素与最后一个元素交换，获取到最大元素（交换后的最后一个元素），将最大元素放到数组末尾
  swap($arr,0,$i); 
  //经过交换，将最后一个元素（最大元素）脱离大根堆，并将未经排序的新树($arr[0...$i-1])重新调整为大根堆
  HeapAdjust($arr,0,$i - 1);
 }
}

$arr = array(9,1,5,8,3,7,4,6,2);
HeapSort($arr);
var_dump($arr);

Zeitkomplexitätsanalyse:

Solange seine Laufzeit beträgt Nehmen Sie sich Zeit, um das erste Build-Paar zu sichten und den Stapel neu aufzubauen.

Insgesamt beträgt die zeitliche Komplexität der Heap-Sortierung O(nlogn). Da die Heap-Sortierung nicht auf den Sortierstatus der Originaldatensätze reagiert, beträgt ihre beste, schlechteste und durchschnittliche Zeitkomplexität O(nlogn). Dies ist offensichtlich in der Leistung weitaus besser als die O(n^2)-Zeitkomplexität von Bubbling, einfacher Auswahl und direkter Einfügung.

Verwandte Empfehlungen:

Detaillierte Erläuterung der Direktauswahlsortierung von PHP-Sortieralgorithmusreihen

Detaillierte Erläuterung der Zusammenführungssortierung des PHP-Sortieralgorithmus

Detaillierte Erläuterung der Bucket-Sortierung des PHP-Sortieralgorithmus series_php skills

Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung des PHP-Sortieralgorithmus Heap-Sortierung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!