Three.js implementiert die gemeinsame Nutzung von 3D-Karteninstanzen-js-Tutorial-php.cn

Dieser Artikel führt Sie hauptsächlich in den praktischen Prozess der Verwendung von Three.js zum Entwickeln und Implementieren von 3D-Karten ein. Der Artikel stellt ihn ausführlich anhand von Beispielcode vor. Er bietet einen gewissen Referenz-Lernwert, damit jeder Three.js lernen oder verwenden kann . Freunde, die es brauchen. Lasst uns mit dem Herausgeber unten lernen. Ich hoffe, es hilft allen.

Vorwort

In diesem Artikel werden hauptsächlich die Entwicklungsgrundlagen und Grundprinzipien von Three.js sowie die Realisierung eines 3D-Panoramas vorgestellt. Wer den Effekt eines 3D-Panoramas im Web erzielen möchte, muss sich neben Panoramabildern und WebGL auch mit vielen Details auseinandersetzen. Soweit ich weiß, ist KrPano derzeit der beste ausländische 3D-Panoramadienst, und viele inländische 3D-Panoramadienste nutzen Krpano-Tools.

Ich habe vor einiger Zeit einen Monat lang gearbeitet und Überstunden gemacht, um ein 3D-Projekt fertigzustellen. Es kann als Übergang von der traditionellen Web- zur Webgl-Grafikentwicklung angesehen werden, und es gibt viele Fallstricke. Ich habe eine Zusammenfassung erstellt und sie geteilt.

Three.js

Mit dem Ziel, die Komplexität der WebGL-Entwicklung zu vereinfachen und die Schwierigkeit des Einstiegs zu verringern, hat mrdoob) eine leichte JS-3D-Bibliothek basierend auf dem WebGL-Standard gekapselt – Three .js .

Meiner Meinung nach hat Three.js die folgenden Eigenschaften:

Es verfügt im Wesentlichen über die vollständigen Funktionen, die für die 3D-Entwicklung erforderlich sind, die mit WebGL erzielt werden können kann mit Three erreicht werden. .js kann einfacher implementiert werden
Das benutzerfreundliche Architekturdesign ist klarer und vernünftiger, leicht zu verstehen, hat eine gute Skalierbarkeit und die Entwicklung Die Effizienz ist höher als bei WebGL
Das Open-Source-Projekt ist Open Source und verfügt über eine Gruppe aktiver Mitwirkender. Es wird kontinuierlich gewartet und aktualisiert

Three.js macht WebGL einfacher zu verwenden und kann tolle 3D-Effekte erzielen, zum Beispiel:

Game hellorun
Datenvisualisierung armsglobe

1. Normalenvektorproblem

Normalen sind Vektoren senkrecht zur Oberfläche des Objekts, das wir beleuchten möchten. Normalen stellen die Richtung einer Oberfläche dar und spielen daher eine entscheidende Rolle bei der Modellierung der Wechselwirkung zwischen Lichtquellen und Objekten. Jedem Scheitelpunkt ist ein Normalenvektor zugeordnet.

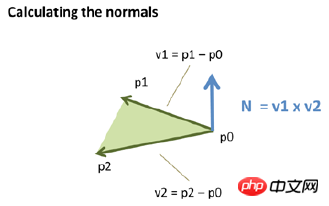
Wenn ein Scheitelpunkt von mehreren Dreiecken gemeinsam genutzt wird, ist der Normalenvektor des gemeinsamen Scheitelpunkts gleich der Summe der Normalenvektoren des gemeinsamen Scheitelpunkts in verschiedenen Dreiecken. N=N1+N2;

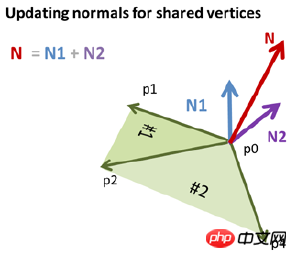
Wenn Sie also keine Verarbeitung durchführen und die Punkte des 3D-Objekts direkt an BufferGeometry übergeben, dann wird der Normalenvektor synthetisiert, es wird durch das Fragment gefärbt. Nach der Interpolation erhalten Sie diesen Schwarz-Weiß-Effekt

Meine Verarbeitungsmethode hält den Normalenvektor des Scheitelpunkts einzigartig, daher müssen Sie ihn kopieren einen Scheitelpunkt am gemeinsamen Scheitelpunkt und berechnen Sie den Index neu. Ja, jeder Scheitelpunkt, der von mehreren Flächen geteilt wird, hat mehrere Kopien, jede Kopie hat einen separaten Normalenvektor, sodass jede Fläche die gleiche Farbe hat

2. Lichtquelle und Oberflächenblockfarbe

Während des Entwicklungsprozesses wurde eine Reihe von Farbkombinationen entworfen. Sobald jedoch eine Lichtquelle vorhanden ist, wird die endgültige Farbe des Oberflächenblocks gemischt Natürlich weicht die Farbe stark vom endgültigen Design ab. Das Folgende ist der Hybridalgorithmus des Lambert-Beleuchtungsmodells.

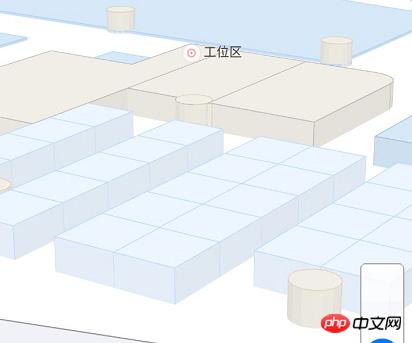
Und die Anforderung des Produkts besteht darin, dass die Oberseite die Designfarbe beibehält und der Lichtquellenwechseleffekt an der Seite hinzugefügt werden muss, wenn die Karte bedient wird , muss sich die Seitenfarbe je nach Betrachtungswinkel ändern. Dann gehe ich damit um, indem ich die obere Fläche und die seitliche Fläche getrennt zeichne (zwei Mesh-Elemente erstellen), um die Selbstbeleuchtungsfarbe auf der oberen Fläche so einzustellen, dass sie mit der Designfarbe übereinstimmt Es entsteht kein Lichteffekt. Verwenden Sie Emssive und die Seitenfläche umfassend, um Lichteffekte anzuwenden.

var material1 = new __WEBPACK_IMPORTED_MODULE_0_three__["MeshLambertMaterial"]({
 emissive: new __WEBPACK_IMPORTED_MODULE_0_three__["Color"](style.fillStyle[0], style.fillStyle[1], style.fillStyle[2]),
 side: __WEBPACK_IMPORTED_MODULE_0_three__["DoubleSide"],
 shading: __WEBPACK_IMPORTED_MODULE_0_three__["FlatShading"],
 vertexColors: __WEBPACK_IMPORTED_MODULE_0_three__["VertexColors"]
 });

 var material2 = new __WEBPACK_IMPORTED_MODULE_0_three__["MeshLambertMaterial"]({
 color: new __WEBPACK_IMPORTED_MODULE_0_three__["Color"](style.fillStyle[0] * 0.1, style.fillStyle[1] * 0.1, style.fillStyle[2] * 0.1),
 emissive: new __WEBPACK_IMPORTED_MODULE_0_three__["Color"](style.fillStyle[0] * 0.9, style.fillStyle[1] * 0.9, style.fillStyle[2] * 0.9),
 side: __WEBPACK_IMPORTED_MODULE_0_three__["DoubleSide"],
 shading: __WEBPACK_IMPORTED_MODULE_0_three__["FlatShading"],
 vertexColors: __WEBPACK_IMPORTED_MODULE_0_three__["VertexColors"]
 });

Nach dem Login kopieren

3. POI-Anmerkung

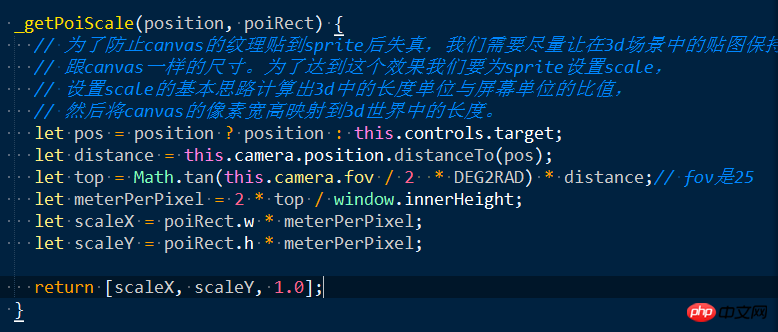
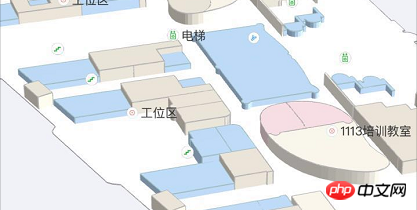
Drei können die Sprite-Klasse verwenden, um einen POI zu erstellen, der immer der Kamera zugewandt ist, und Sie können Text zeichnen und Bilder auf der Leinwand platzieren. Platzieren Sie die Leinwand als Texturkarte auf dem Sprite. Ein Problem hierbei ist jedoch, dass das Leinwandbild verzerrt wird. Der Grund dafür ist, dass der Maßstab des Sprites nicht richtig eingestellt ist, wodurch das Bild gestreckt oder skaliert und verzerrt wird.

Die Lösung des Problems besteht darin, sicherzustellen, dass die Zoomgröße in der 3D-Welt nach einer Reihe von Transformationen und Projektionen mit der Größe der Leinwand auf dem Bildschirm übereinstimmt dem Kamerabildschirm. Dazu müssen wir das Verhältnis von Bildschirmpixeln zu Längeneinheiten in der 3D-Welt berechnen und dann das Sprite auf die entsprechende 3D-Länge skalieren.

4. Click-to-Pick-Problem

Das Zeichnen von 3D-Objekten auf dem Bildschirm in Webgl geht durch die folgenden Phasen

所以要在3D应用做点击拾取，首先要将屏幕坐标系转化成ndc坐标系，这时候得到ndc的xy坐标，由于2d屏幕并没有z值所以，屏幕点转化成3d坐标的z可以随意取值，一般取0.5（z在-1到1之间

function fromSreenToNdc(x, y, container) {
 return {
 x: x / container.offsetWidth * 2 - 1,
 y: -y / container.offsetHeight * 2 + 1,
 z: 1
 };
}
function fromNdcToScreen(x, y, container) {
 return {
 x: (x + 1) / 2 * container.offsetWidth,
 y: (1 - y) / 2 * container.offsetHeight
 };
}

Nach dem Login kopieren

然后将ndc坐标转化成3D坐标：　　ndc = P * MV * Vec4　　Vec4 = MV-1 * P -1 * ndc　　这个过程在Three中的Vector3类中已经有实现：

unproject: function () {

 var matrix = new Matrix4();

 return function unproject( camera ) {

 matrix.multiplyMatrices( camera.matrixWorld, matrix.getInverse( camera.projectionMatrix ) );
 return this.applyMatrix4( matrix );

 };

 }(),

Nach dem Login kopieren

将得到的3d点与相机位置结合起来做一条射线，分别与场景中的物体进行碰撞检测。首先与物体的外包球进行相交性检测，与球不相交的排除，与球相交的保存进入下一步处理。将所有外包球与射线相交的物体按照距离相机远近进行排序，然后将射线与组成物体的三角形做相交性检测。求出相交物体。当然这个过程也由Three中的RayCaster做了封装，使用起来很简单：

mouse.x = ndcPos.x;
 mouse.y = ndcPos.y;

 this.raycaster.setFromCamera(mouse, camera);

 var intersects = this.raycaster.intersectObjects(this._getIntersectMeshes(floor, zoom), true);

Nach dem Login kopieren

5、性能优化

随着场景中的物体越来越多，绘制过程越来越耗时，导致手机端几乎无法使用。

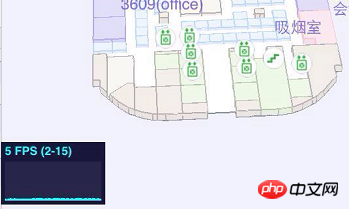
在图形学里面有个很重要的概念叫“one draw all”一次绘制，也就是说调用绘图api的次数越少，性能越高。比如canvas中的fillRect、fillText等，webgl中的drawElements、drawArrays；所以这里的解决方案是对相同样式的物体，把它们的侧面和顶面统一放到一个BufferGeometry中。这样可以大大降低绘图api的调用次数，极大的提升渲染性能。

这样解决了渲染性能问题，然而带来了另一个问题，现在是吧所有样式相同的面放在一个BufferGeometry中（我们称为样式图形），那么在面点击时候就无法单独判断出到底是哪个物体（我们称为物体图形）被选中，也就无法对这个物体进行高亮缩放处理。我的处理方式是，把所有的物体单独生成物体图形保存在内存中，做面点击的时候用这部分数据来做相交性检测。对于选中物体后的高亮缩放处理，首先把样式面中相应部分裁减掉，然后把选中的物体图形加入到场景中，对它进行缩放高亮处理。裁剪方法是，记录每个物体在样式图形中的其实索引位置，在需要裁切时候将这部分索引制零。在需要恢复的地方在把这部分索引恢复成原状。

6、面点击移动到屏幕中央

这部分也是遇到了不少坑，首先的想法是：

面中心点目前是在世界坐标系内的坐标，先用center.project（camera）得到归一化设备坐标，在根据ndc得到屏幕坐标，而后根据面中心点屏幕坐标与屏幕中心点坐标做插值，得到偏移量，在根据OribitControls中的pan方法来更新相机位置。这种方式最终以失败告终，因为相机可能做各种变换，所以屏幕坐标的偏移与3d世界坐标系中的位置关系并不是线性对应的。　　

最终的想法是：　　

我们现在想将点击面的中心点移到屏幕中心，屏幕中心的ndc坐标永远都是（0,0）我们的观察视线与近景面的焦点的ndc坐标也是0,0；也就是说我们要将面中心点作为我们的观察点（屏幕的中心永远都是相机的观察视线），这里我们可以直接将面中心所谓视线的观察点，利用lookAt方法求取相机矩阵，但如果这样简单处理后的效果就会给人感觉相机的姿态变化了，也就是会感觉并不是平移过去的，所以我们要做的是保持相机当前姿态将面中心作为相机观察点。　　

回想平移时我们将屏幕移动转化为相机变化的过程是知道屏幕偏移求target，这里我们要做的就是知道target反推屏幕偏移的过程。首先根据当前target与面中心求出相机的偏移向量，根据相机偏移向量求出在相机x轴和up轴的投影长度，根据投影长度就能返推出应该在屏幕上的平移量。　

this.unprojectPan = function(deltaVector, moveDown) {
 // var getProjectLength()
 var element = scope.domElement === document ? scope.domElement.body : scope.domElement;

 var cxv = new Vector3(0, 0, 0).setFromMatrixColumn(scope.object.matrix, 0);// 相机x轴
 var cyv = new Vector3(0, 0, 0).setFromMatrixColumn(scope.object.matrix, 1);// 相机y轴
 // 相机轴都是单位向量
 var pxl = deltaVector.dot(cxv)/* / cxv.length()*/; // 向量在相机x轴的投影
 var pyl = deltaVector.dot(cyv)/* / cyv.length()*/; // 向量在相机y轴的投影

 // offset=dx * vector(cx) + dy * vector(cy.project(xoz).normalize)
 // offset由相机x轴方向向量+相机y轴向量在xoz平面的投影组成
 var dv = deltaVector.clone();
 dv.sub(cxv.multiplyScalar(pxl));
 pyl = dv.length();

 if ( scope.object instanceof PerspectiveCamera ) {
 // perspective

 var position = scope.object.position;
 var offset = new Vector3(0, 0, 0);
 offset.copy(position).sub(scope.target);
 var distance = offset.length();
 distance *= Math.tan(scope.object.fov / 2 * Math.PI / 180);

 // var xd = 2 * distance * deltaX / element.clientHeight;
 // var yd = 2 * distance * deltaY / element.clientHeight;
 // panLeft( xd, scope.object.matrix );
 // panUp( yd, scope.object.matrix );

 var deltaX = pxl * element.clientHeight / (2 * distance);
 var deltaY = pyl * element.clientHeight / (2 * distance) * (moveDown ? -1 : 1);

 return [deltaX, deltaY];
 } else if ( scope.object instanceof OrthographicCamera ) {

 // orthographic
 // panLeft( deltaX * ( scope.object.right - scope.object.left ) / scope.object.zoom / element.clientWidth, scope.object.matrix );
 // panUp( deltaY * ( scope.object.top - scope.object.bottom ) / scope.object.zoom / element.clientHeight, scope.object.matrix );
 var deltaX = pxl * element.clientWidth * scope.object.zoom / (scope.object.right - scope.object.left);
 var deltaY = pyl * element.clientHeight * scope.object.zoom / (scope.object.top - scope.object.bottom);

 return [deltaX, deltaY];
 } else {

 // camera neither orthographic nor perspective
 console.warn( 'WARNING: OrbitControls.js encountered an unknown camera type - pan disabled.' );

 }
 }

Nach dem Login kopieren

7、2/3D切换

23D切换的主要内容就是当相机的视线轴与场景的平面垂直时，使用平行投影，这样用户只能看到顶面给人的感觉就是2D视图。所以要根据透视的视锥体计算出平行投影的世景体。

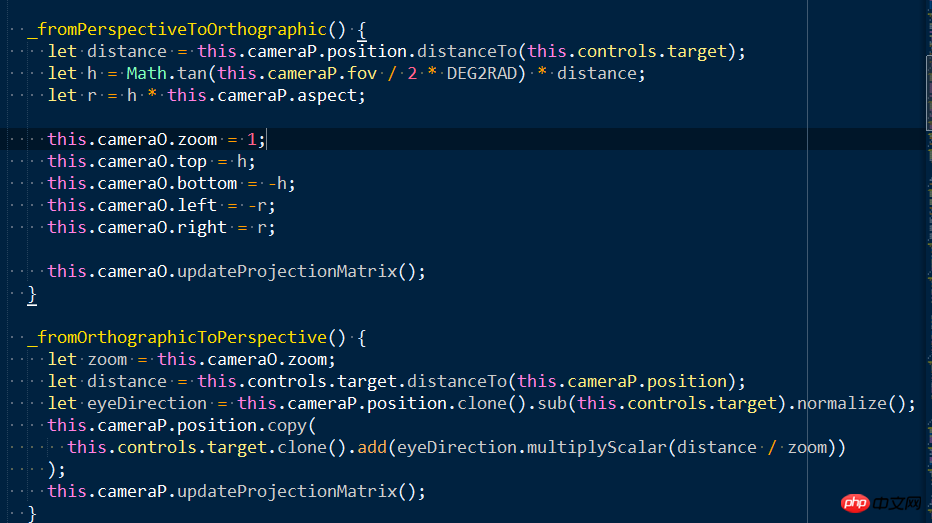
因为用户会在2D、3D场景下做很多操作，比如平移、缩放、旋转，要想无缝切换，这个关键在于将平行投影与视锥体相机的位置、lookAt方式保持一致；以及将他们放大缩小的关键点：distance的比例与zoom来保持一致。

平行投影中，zoom越大代表六面体的首尾两个面面积越小，放大越大。

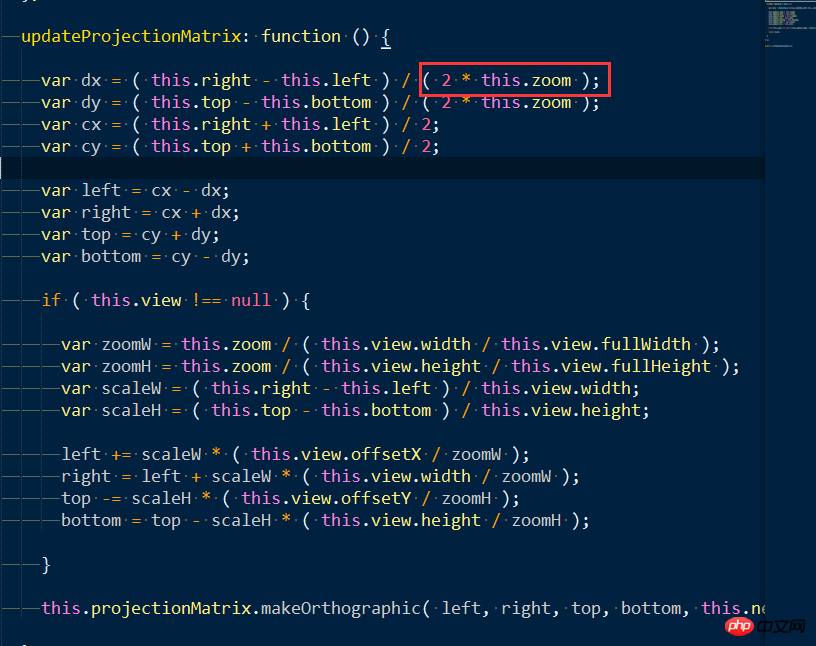
8、3D中地理级别　　

地理级别实际是像素跟墨卡托坐标系下米的对应关系，这个有通用的标准以及计算公式：

r=6378137
resolution=2*PI*r/(2^zoom*256)

Nach dem Login kopieren

各个级别中像素与米的对应关系如下：

resolution zoom 2048 blocksize 256 blocksize scale(dpi=160)
156543.0339 0 320600133.5 40075016.69 986097851.5
78271.51696 1 160300066.7 20037508.34 493048925.8
39135.75848 2 80150033.37 10018754.17 246524462.9
19567.87924 3 40075016.69 5009377.086 123262231.4
9783.939621 4 20037508.34 2504688.543 61631115.72
4891.96981 5 10018754.17 1252344.271 30815557.86
2445.984905 6 5009377.086 626172.1357 15407778.93
1222.992453 7 2504688.543 313086.0679 7703889.465
611.4962263 8 1252344.271 156543.0339 3851944.732
305.7481131 9 626172.1357 78271.51696 1925972.366
152.8740566 10 313086.0679 39135.75848 962986.1831
76.4370283 11 156543.0339 19567.87924 481493.0916
38.2185141 12 78271.51696 9783.939621 240746.5458
19.1092571 13 39135.75848 4891.96981 120373.2729
9.5546285 14 19567.87924 2445.984905 60186.63645
4.7773143 15 9783.939621 1222.992453 30093.31822
2.3886571 16 4891.96981 611.4962263 15046.65911
1.1943286 17 2445.984905 305.7481131 7523.329556
0.5971643 18 1222.992453 152.8740566 3761.664778
0.2985821 19 611.4962263 76.43702829 1880.832389
0.1492911 20 305.7481131 38.21851414 940.4161945
0.0746455 21
0.0373227 22

Nach dem Login kopieren

3D中的计算策略是，首先需要将3D世界中的坐标与墨卡托单位的对应关系搞清楚，如果已经是以mi来做单位，那么就可以直接将相机的投影屏幕的高度与屏幕的像素数目做比值，得出的结果跟上面的ranking做比较，选择不用的级别数据以及比例尺。注意3D地图中的比例尺并不是在所有屏幕上的所有位置与现实世界都满足这个比例尺，只能说是相机中心点在屏幕位置处的像素是满足这个关系的，因为平行投影有近大远小的效果。

9、poi碰撞

由于标注是永远朝着相机的，所以标注的碰撞就是把标注点转换到屏幕坐标系用宽高来计算矩形相交问题。至于具体的碰撞算法，大家可以在网上找到，这里不展开。下面是计算poi矩形的代码

export function getPoiRect(poi, zoomLevel, wrapper) {
 let style = getStyle(poi.styleId, zoomLevel);
 if (!style) {
 console.warn("style is invalid!");
 return;
 }
 let labelStyle = getStyle(style.labelid, zoomLevel);
 if (!labelStyle) {
 console.warn("labelStyle is invalid!");
 return;
 }
 if (!poi.text) {
 return;
 }
 let charWidth = (TEXTPROP.charWidth || 11.2) * // 11.2是根据测试得到的估值
 (labelStyle.fontSize / (TEXTPROP.fontSize || 13)); // 13是得到11.2时的fontSize
 // 返回2d坐标
 let x = 0;//poi.points[0].x;
 let y = 0;//-poi.points[0].z;
 let path = [];
 let icon = iconSet[poi.styleId];
 let iconWidh = (icon && icon.width) || 32;
 let iconHeight = (icon && icon.height) || 32;
 let multi = /\//g;
 let firstLinePos = [];
 let textAlign = null;
 let baseLine = null;
 let hOffset = (iconWidh / 2) * ICONSCALE;
 let vOffset = (iconHeight / 2) * ICONSCALE;
 switch(poi.direct) {
 case 2: { // 左
 firstLinePos.push(x - hOffset - 2);
 firstLinePos.push(y);
 textAlign = 'right';
 baseLine = 'middle';
 break;
 };
 case 3: { // 下
 firstLinePos.push(x);
 firstLinePos.push(y - vOffset - 2);
 textAlign = 'center';
 baseLine = 'top';
 break;
 };
 case 4: { // 上
 firstLinePos.push(x);
 firstLinePos.push(y + vOffset + 2);
 textAlign = 'center';
 baseLine = 'bottom';
 break;
 };
 case 1:{ // 右
 firstLinePos.push(x + hOffset + 2);
 firstLinePos.push(y);
 textAlign = 'left';
 baseLine = 'middle';
 break;
 };
 default: {
 firstLinePos.push(x);
 firstLinePos.push(y);
 textAlign = 'center';
 baseLine = 'middle';
 }
 }
 path = path.concat(firstLinePos);

 let minX = null, maxX = null;
 let minY = null, maxY = null;
 let parts = poi.text.split(multi);

 let textWidth = 0;
 if (wrapper) {
 // 汉字和数字的宽度是不同的，所以必须使用measureText来精确测量
 let textWidth1 = wrapper.context.measureText(parts[0]).width;
 let textWidth2 = wrapper.context.measureText(parts[1] || '').width;
 textWidth = Math.max(textWidth1, textWidth2);
 } else {
 textWidth = Math.max(parts[0].length, parts[1] ? parts[1].length : 0) * charWidth;
 }

 if (textAlign === 'left') {
 minX = x - hOffset;
 maxX = path[0] + textWidth; // 只用第一行文本
 } else if (textAlign === 'right') {
 minX = path[0] - textWidth;
 maxX = x + hOffset;
 } else { // center
 minX = x - Math.max(textWidth / 2, hOffset);
 maxX = x + Math.max(textWidth / 2, hOffset);
 }
 if (baseLine === 'top') {
 maxY = y + vOffset;
 minY = y - vOffset - labelStyle.fontSize * parts.length;
 } else if (baseLine === 'bottom') {
 maxY = y + vOffset + labelStyle.fontSize * parts.length;
 minY = y - vOffset;
 } else { // middle
 minY = Math.min(y - vOffset, path[1] - labelStyle.fontSize / 2);
 maxY = Math.max(y + vOffset, path[1] + labelStyle.fontSize * (parts.length + 0.5 - 1));
 }

 return {
 min: {
 x: minX,
 y: minY
 },
 max: {
 x: maxX,
 y: maxY
 }
 };
}

Nach dem Login kopieren

大家学会了吗？赶紧动尝试一下吧。