
Dieser Artikel führt Sie hauptsächlich in die relevanten Informationen zur Verwendung von CSS ein, um Pfeilbeispiele jeder Größe, jeder Richtung und jedes Winkels zu realisieren. Jetzt werde ich es mit Ihnen teilen und Ihnen eine Referenz geben. Ich hoffe, es kann für alle hilfreich sein.
In der Webentwicklung wird häufig der Dropdown-Pfeil

und der Rechtspfeil

So ein Pfeil. Es wird im Allgemeinen mit CSS implementiert:
{
display: inline-block;
margin: 72px;
border-top: 24px solid;
border-right: 24px solid;
width: 120px;
height: 120px;
transform: rotate(45deg);
}, da dies durch die Verwendung von border-top und border-right von p und anschließendes Drehen des p erreicht wird.
Pfeile in jedem Winkel
Hier ist eine Frage: Was ist, wenn Sie einen Pfeil mit einem Winkel von 120 Grad benötigen? Da „Rand oben“ und „Rand rechts“ immer 90 Grad betragen, funktioniert eine einfache Drehung nicht. Wir können p zunächst um 45 Grad drehen, um daraus eine Raute zu machen, und es dann in einen beliebigen Winkel strecken, sodass wir in jedem Winkel einen Pfeil erhalten. Da zwei Transformationen, Rotation und Skalierung, verwendet werden, muss die Transformationsmatrix transform: matrix(a,b,c,d,e,f) verwendet werden. Die 6 Variablen bilden hier eine dreidimensionale Transformationsmatrix
Die Translation, Rotation, Expansionstransformation und verschiedene Kombinationen eines beliebigen Punktes p (x, y) können durch diese Transformationsmatrix erreicht werden:
Hinweis: Zur Darstellung eines Punktes werden hier homogene Koordinaten verwendet. Einfach ausgedrückt wird p(x, y) ausgedrückt als p'(x', y', 1)
Übersetzungsmatrix
v(x, y) verschiebt tx entlang der x-Achse , entlang Verschieben Sie ty entlang der y-Achse. Dann gibt es:
x' = x + tx
y' = y + ty
Also die Übersetzungsmatrix:
Rotationsmatrix
v(x, y)-Punkt dreht θ um den Ursprung zu v'(x', y')
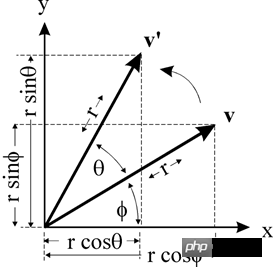
dann Es gilt:
x = r * cos(ϕ )
y = r * sin(ϕ )x' = r * cos(θ + ϕ) = r * cos(θ ) * cos(ϕ) - r * sin(θ) * sin(ϕ ) // Kosinusformel
y' = r * sin(θ + ϕ) = r * sin(θ) * cos( ϕ) + r * cos(θ) * sin(ϕ ) // Sinusformel
Also:
x' = x * cos(θ) - y * sin(θ)
y' = x * sin(θ) + y * cos(θ)
Also die Rotationsmatrix:
Streckmatrix
Angenommen, die Expansions- und Kontraktionsverhältnisse der x-Achse und der y-Achse sind kx bzw. ky. Dann gibt es:
x' = x * kx
y' = y * ky
Also:
Zusammengesetzte Transformation
Was wäre, wenn p(x, y) zuerst verschoben (Transformationsmatrix A), dann gedreht (Transformationsmatrix B) und dann gestreckt (Transformationsmatrix C) wird?
S ' =C(B(Ap)) ==> p' = (CBA)p //Matrixmultiplikationskombinationsrate
Jetzt ist der Pfeil in jedem Winkel o sehr einfach:
Zuerst p wird um 45 Grad gedreht, um eine Raute zu werden, umgewandelt in M1 Teleskopische X-Achse, Y-Achse:
x' = size * cos(o/2) = x * √2 * cos(o/2) y' = size * sin(o/2) = y * √2 * sin(o/2)
Das ist: kx = √2 * cos( o/2); ky = √2 * sin(o/2) Auf diese Weise erhält man einen Pfeil in einem beliebigen Winkel. Verwandeln Sie sich in M2
Wenn die Richtung des Pfeils nicht nach rechts zeigt, können Sie durch eine Drehung einen Pfeil in jede beliebige Richtung erhalten. In M3
transformieren. Aufgrund von p' =C(B(Ap)) ==> p' = (CBA)p können wir dann zuerst M3 M2 M1 berechnen und dann die entsprechende Transformation für p durchführen, um einen beliebigen Winkel zu erhalten Pfeil in eine beliebige Richtung.
Die Breite und Höhe von p sind die Seitenlängen des Pfeils. Durch Anpassen können Sie einen Pfeil mit beliebiger Seitenlänge erhalten.
React-Komponente
Aus Gründen der Benutzerfreundlichkeit ist dieser Pfeil als React-Komponente gekapselt.
Beispiel
Einfacher Pfeil

Auswahl simulieren

Abweichende Pfeile

Requisiten
| name | type | default | description |
|---|---|---|---|
| degree | number | 90 | 箭头的张角, 角度制 |
| offsetDegree | number | 0 | 箭头的方向,默认指向右边 |
| color | string | - | 箭头的颜色 |
| size | string | 10px | 箭头边长 |
安装使用
npm install rc-arrow --save
import Arrow from 'rc-arrow'
class Hw extends Component {
render() {
return (
<Arrow size="20px" color="red"/>
)
}
}相关推荐:
Das obige ist der detaillierte Inhalt vonCSS implementiert Pfeilcode beliebiger Größe, Richtung und Winkel. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




