
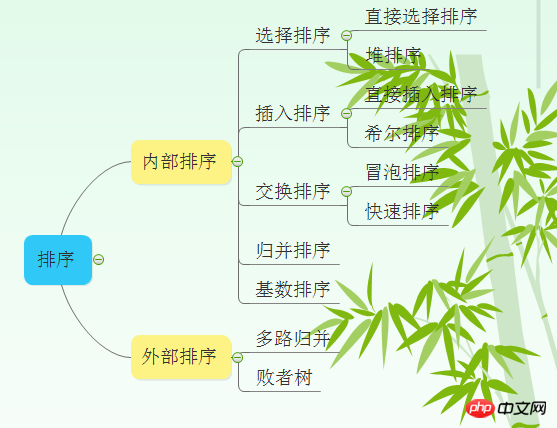
Austauschsortierung: Die Grundidee der Austauschsortierung besteht darin, die Schlüsselwerte zweier Datensätze zu vergleichen. Wenn die Schlüsselwerte der beiden Datensätze in umgekehrter Reihenfolge sind, werden die beiden Datensätze ausgetauscht, sodass der Datensatz entsteht mit dem kleineren Schlüsselwert wird in die entgegengesetzte Richtung verschoben, und Datensätze mit größeren Schlüsselwerten werden an das Ende der Sequenz verschoben.
1. Blasensortierung
Einführung:
Bubble Sort (Bubble Sort, übersetzt aus Taiwan als: Bubble Sort oder Blasensortierung) ist ein einfacher Sortieralgorithmus . Es durchläuft wiederholt die zu sortierende Sequenz, vergleicht jeweils zwei Elemente und vertauscht sie, wenn sie in der falschen Reihenfolge sind. Der Besuch des Arrays wird wiederholt, bis kein Austausch mehr erforderlich ist, was bedeutet, dass das Array sortiert wurde. Der Name dieses Algorithmus rührt von der Tatsache her, dass kleinere Elemente durch den Austausch langsam an die Spitze des Arrays „schweben“.
Schritte:
Benachbarte Elemente vergleichen. Wenn das erste größer als das zweite ist, tauschen Sie beide aus.
Machen Sie dasselbe für jedes Paar benachbarter Elemente, vom ersten Paar am Anfang bis zum letzten Paar am Ende. Zu diesem Zeitpunkt sollte das letzte Element die größte Zahl sein.
Wiederholen Sie die obigen Schritte für alle Elemente außer dem letzten.
Wiederholen Sie die obigen Schritte jedes Mal für immer weniger Elemente, bis keine Zahlenpaare mehr zum Vergleichen vorhanden sind.
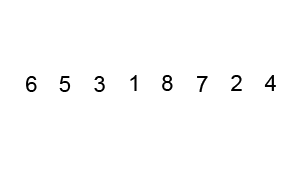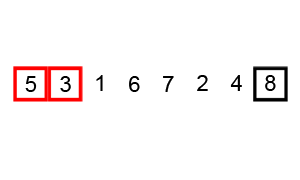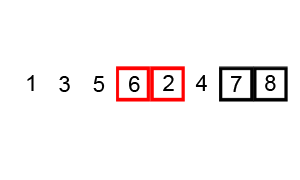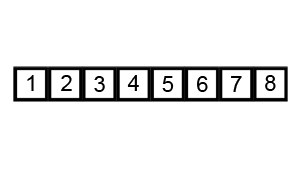
Blasensortierung ist am einfachsten zu verstehen, aber die zeitliche Komplexität ist ( O(n^2)) ist auch einer der größten. Der Implementierungscode lautet wie folgt:
<br/>
$arr=array(1,43,54,62,21 ,66,32,78,36,76,39); $arr
){
$lencount
(); //Legen Sie ein leeres Array fest, um auftauchende Blasen zu empfangen
//Diese Ebenenschleife steuert die Anzahl der Runden, die gesprudelt werden müssen
für($i
=1;<$len;$i++) { //Diese Schleifenebene wird verwendet, um zu steuern, wie oft eine Zahl in jeder Runde verglichen werden muss
für($k=0;$k<$len-$i;$k ++)
{
if ($arr[$k]>$arr [$k+1])
{
$tmp=$arr[$k +1];
$arr[$k+1] =$arr[$k];
$arr[$k]=$tmp; 🎜>
$ arr
} >2. Schnelle Sortierung Einführung: Quick Sort wurde von
Tony HallElementen Ο(
n) Vergleiche. Im schlimmsten Fall sind Ο(n2) Vergleiche erforderlich, aber diese Situation ist ungewöhnlich. Tatsächlich ist die schnelle Sortierung normalerweise deutlich schneller als andere
Ο(n log
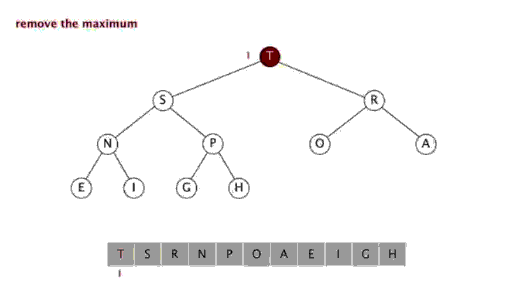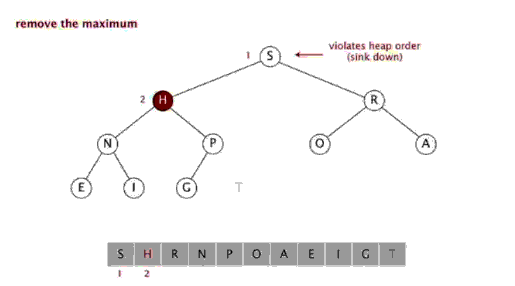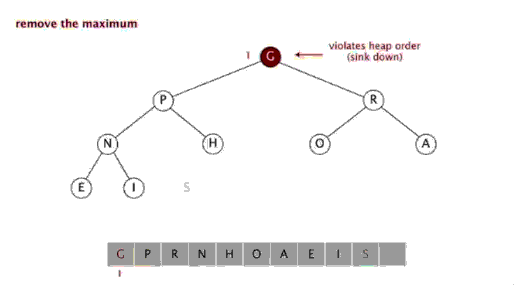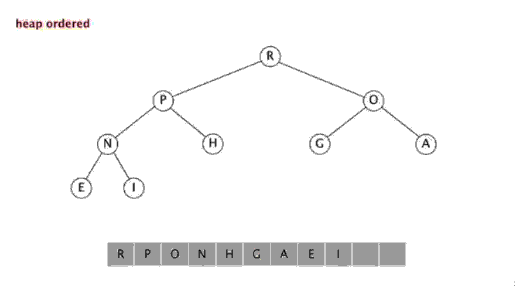
n)-Algorithmen, da ihre innere Schleife in den meisten Architekturen sehr gut implementiert werden kann effizient und in den meisten realen Daten kann die Möglichkeit eines quadratischen Termes die Entwurfsauswahl bestimmen und den Zeitaufwand reduzieren. Schritte: Wählen Sie ein Element aus der Sequenz aus, das als „Pivot“ bezeichnet wird. Ordnen Sie die Sequenz neu, alle Elemente Elemente, die kleiner als der Basiswert sind, werden vor der Basis platziert, und alle Elemente, die größer als der Basiswert sind, werden hinter der Basis platziert (die gleiche Anzahl kann auf beiden Seiten platziert werden). Nachdem diese Partition beendet wurde, befindet sich die Basis in der Mitte der Sequenz. Dies wird als Partition -Vorgang bezeichnet. Rekursiv sortieren Sie das Subarray der Elemente, die kleiner als der Basiswert sind, und das Subarray der Elemente, die größer als der Basiswert sind. Schnellsortierung ist ebenfalls ein effizienter Sortieralgorithmus, und seine zeitliche Komplexität beträgt ebenfalls O( nlogn). Der Code lautet wie folgt: function quick_sort($arr ) { //Bestimmen Sie zunächst, ob Sie fortfahren müssen $length = count($arr); ) { zurück $arr; } 🎜> //Wählen Sie ein Lineal aus //Wählen Sie das erste Element aus $base_num = $arr [0]; //Alle Elemente außer dem Lineal durchlaufen und entsprechend ihrer Größe in zwei Arrays einteilen //Zwei Arrays initialisieren $left_array = array();// kleiner als das Lineal $right_array = array ();// größer als das Lineal für($i=1; $i<$length; $i++) { if($base_num > $arr[$i]) { 🎜> $left_array[] = $arr[$i]; { $right_array[] = $arr[$i]; > //Dann Führen Sie den gleichen Sortiervorgang für das linke bzw. rechte Array aus // Rufen Sie diese Funktion rekursiv auf und zeichnen Sie sie auf das Ergebnis $left_array ); $right_array ); //Füge das linke und das rechte Lineal zusammen return array_merge($left_array , array($base_num), $right_array); } Sortieren auswählen Die Auswahlsortierung umfasst zwei Arten, nämlich die direkte Auswahlsortierung und die Heap-Sortierung. Die Grundidee der Auswahlsortierung besteht darin, dass jedes Mal n- i+ Wählen Sie den Datensatz mit dem kleinsten Schlüsselwert unter 1 (i=1,2,3,...,n-1) Datensätzen als i-ten Datensatz in der geordneten Reihenfolge aus 3. Auswahlsortierung Einführung: Auswahlsortierung ist ein einfacher und intuitiver Sortieralgorithmus. So funktioniert es. Suchen Sie zunächst das kleinste Element in der unsortierten Sequenz und speichern Sie es am Anfang der sortierten Sequenz. Suchen Sie dann weiterhin das kleinste Element aus den verbleibenden unsortierten Elementen und fügen Sie es dann am Ende der sortierten Sequenz ein. Und so weiter, bis alle Elemente sortiert sind. [php]einfach anzeigenkopieren <br/> Funktion select_sort($arr) { //Implementierungsidee: Die Doppelschleife ist abgeschlossen, die äußere Schicht steuert die Anzahl der Runden und den aktuellen Mindestwert. Die Anzahl der von der inneren Ebene gesteuerten Vergleiche //$i Die Position des aktuellen Minimalwerts , die am Vergleich teilnehmen müssen Elemente =0, $len =count($arr) ; $i<$len-1; $i++ ) { $p = $i; für($j=$i+1; $j<$len; 🎜> 🎜> ] $arr[ //Vergleichen, finden der kleinere, notieren Sie die Position des Minimalwerts und im nächsten Vergleich // Zum Vergleich sollte der bekannte Mindestwert herangezogen werden. } 🎜 > //Die aktuelle Minimalwertposition wurde ermittelt und in $p gespeichert. //Wenn festgestellt wird, dass die Position des Minimalwerts von der aktuell angenommenen Position abweicht $i, die Positionen schließen sich gegenseitig aus. Ändern Sie einfach 🎜> != $i) { 🎜> = [$p]; $arr [ ] = $arr [$i]; > $i] = ; //Zurück zum Endergebnis zurück $arr; } 4. Heap-Sortierung <br/> Heap entwickelt wurde. Der Heap ist eine ungefähre vollständige Binärbaumstruktur Struktur und erfüllt gleichzeitig die Heap-Eigenschaft: das heißt, Die untergeordneten Knoten Ein Schlüssel oder Index ist immer kleiner (oder größer) als sein übergeordneter Knoten. Heap-Sortierung bezieht sich auf einen Sortieralgorithmus, der unter Verwendung einer Datenstruktur wie einem gestapelten Baum (Heap) entwickelt wurde. Verwenden der Eigenschaften von Arrays, um das Element schnell am angegebenen Index zu finden. Der Heap ist in einen großen Root-Heap und einen kleinen Root-Heap unterteilt, bei denen es sich um einen vollständigen Binärbaum handelt. Die Anforderung eines großen Root-Heaps besteht darin, dass der Wert jedes Knotens nicht größer ist als der Wert seines übergeordneten Knotens, d. h. A[PARENT[i]] >= A[i]. Bei der nicht absteigenden Sortierung eines Arrays muss ein großer Root-Heap verwendet werden, da gemäß den Anforderungen eines großen Root-Heaps der Maximalwert oben im Heap liegen muss. 堆排序是一种高效的排序算法,它的时间复杂度是O(nlogn)。原理是:先把数组转为一个最大堆,然后把第一个元素跟第i元素交换,然后把剩下的i-1个元素转为最大堆,然后再把第一个元素与第i-1个元素交换,以此类推。实现代码如下: <br/> <br/> 插入排序 五、插入排序 介绍: 插入排序(Insertion Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。 步骤: 从第一个元素开始,该元素可以认为已经被排序 取出下一个元素,在已经排序的元素序列中从后向前扫描 如果该元素(已排序)大于新元素,将该元素移到下一位置 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置 将新元素插入到该位置中 重复步骤2 [php]einfach anzeigenkopieren <br/> function insert_sort($arr) { //Unterscheiden Sie, welcher Teil sortiert wurde / /Welches Teil ist nicht sortiert //Finden Sie eines der Elemente, das sortiert werden muss //Dieses Element beginnt beim zweiten Element und endet mit dem letzten Element, das sortiert werden muss //Schleife verwenden, um es zu markieren //i-Schleife steuert die Elemente, die jedes Mal eingefügt werden müssen. Sobald die Elemente gesteuert werden, die eingefügt werden müssen, //Indirekt wurde das Array in 2 Teile geteilt, der Index ist kleiner als der aktuelle (linke), es ist die sortierte Reihenfolge for($i=1, $len=count($arr); $i< ;$len; $i++) { //Erhalten Sie den aktuellen Elementwert, der verglichen werden muss. [$i]; Vergleichen und einfügen 🎜> =$i >=0;$j --) { //$arr[$i];//Elemente, die eingefügt werden müssen; $arr[$j];//Elemente, die verglichen werden müssen >]) { Elemente werden mit den vorherigen Elementen vertauscht $arr[$j [ $j] = $tmp; } else { //如果碰到不需要移动的元素 //由于是已经排序好是数组,则前面的就不需要再次比较了。 break; } } } //将这个元素 插入到已经排序好的序列内。 //返回 return $arr; } 六、希尔排序 介绍: 希尔排序,也称递减增量排序算法,是插入排序的一种高速而稳定的改进版本。 希尔排序是基于插入排序的以下两点性质而提出改进方法的: 1、插入排序在对几乎已经排好序的数据操作时, 效率高, 即可以达到线性排序的效率 2、但插入排序一般来说是低效的, 因为插入排序每次只能将数据移动一位> 排序效果: <br/> 七、归并排序 介绍: 归并排序(Merge sort,台湾译作:合并排序)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(pide and Conquer)的一个非常典型的应用 步骤: 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列 设定两个指针,最初位置分别为两个已经排序序列的起始位置 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置 重复步骤3直到某一指针达到序列尾 将另一序列剩下的所有元素直接复制到合并序列尾 排序效果: 我们先来看看主函数部分: 在总函数中,我们只调用了一个 MSort() 函数,因为我们要使用递归调用,所以将 MSort() 封装起来。 下面我们来看看 MSort() 函数: 上面的 MSort() 函数实现将数组分半再分半(直到子序列长度为1),然后将子序列合并起来。 现在是我们的归并操作函数 Merge() : 到了这里,我们的归并算法就完了。我们调用试试: 相关推荐: Das obige ist der detaillierte Inhalt vonPHP implementiert mehrere gängige Sortieralgorithmen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!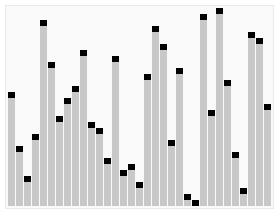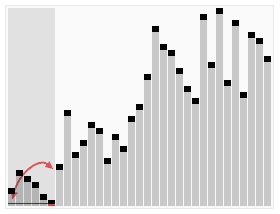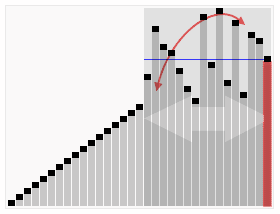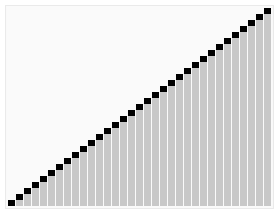
 <br/>
<br/><br/>
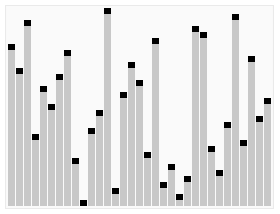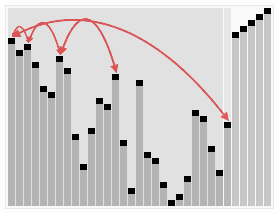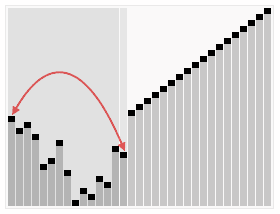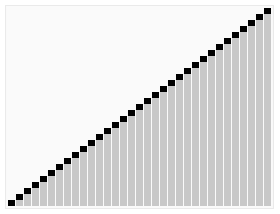 <br/>
<br/>function heapSort($arr) {
$len = count($arr); // 先建立最大堆
for ($i = floor(($len - 1) / 2); $i >= 0; $i--) { $s = $i; $childIndex = $s * 2 + 1; while ($childIndex < $len) { // 在父、左子、右子中 ,找到最大的
if ($childIndex + 1 < $len && $arr[$childIndex] < $arr[$childIndex + 1]) $childIndex++; if ($arr[$s] < $arr[$childIndex]) { $t = $arr[$s]; $arr[$s] = $arr[$childIndex]; $arr[$childIndex] = $t; $s = $childIndex; $childIndex = $childIndex * 2 + 1;
} else { break;
}
}
} // 从最后一个元素开始调整
for ($i = $len - 1; $i > 0; $i--) { $t = $arr[$i]; $arr[$i] = $arr[0]; $arr[0] = $t; // 调整第一个元素
$s = 0; $childIndex = 1; while ($childIndex < $i) { // 在父、左子、右子中 ,找到最大的
if ($childIndex + 1 < $i && $arr[$childIndex] < $arr[$childIndex + 1]) $childIndex++; if ($arr[$s] < $arr[$childIndex]) { $t = $arr[$s]; $arr[$s] = $arr[$childIndex]; $arr[$childIndex] = $t; $s = $childIndex; $childIndex = $childIndex * 2 + 1;
} else { break;
}
}
} return $arr;
}$arr = [3,1,13,5,7,11,2,4,14,9,15,6,12,10,8];
print_r(bubbleSort($arr));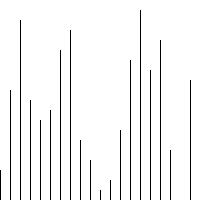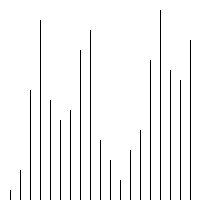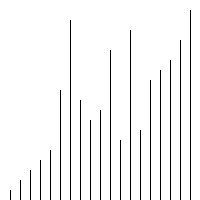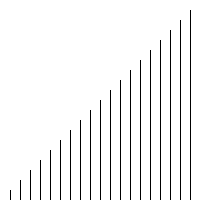 <br/>感觉插入排序跟冒泡排序有点相似,时间复杂度也是O(n^2),实现代码如下:
<br/>感觉插入排序跟冒泡排序有点相似,时间复杂度也是O(n^2),实现代码如下:<br/>
 <br/>希尔排序其实可以理解是插入排序的一个优化版,它的效率跟增量有关,增量要取多少,根据不同的数组是不同的,所以希尔排序是一个不稳定的排序算法,它的时间复杂度为O(nlogn)到O(n^2)之间,实现代码如下:
<br/>希尔排序其实可以理解是插入排序的一个优化版,它的效率跟增量有关,增量要取多少,根据不同的数组是不同的,所以希尔排序是一个不稳定的排序算法,它的时间复杂度为O(nlogn)到O(n^2)之间,实现代码如下:function shellSort($arr) {
$len = count($arr); $stepSize = floor($len / 2); while ($stepSize >= 1) { for ($i = $stepSize; $i < $len; $i++) { if ($arr[$i] < $arr[$i - $stepSize]) { $t = $arr[$i]; $j = $i - $stepSize; while ($j >= 0 && $t < $arr[$j]) { $arr[$j + $stepSize] = $arr[$j]; $j -= $stepSize;
} $arr[$j + $stepSize] = $t;
}
} // 缩小步长,再进行插入排序
$stepSize = floor($stepSize / 2);
} return $arr;
}$arr = [3,1,13,5,7,11,2,4,14,9,15,6,12,10,8];
print_r(bubbleSort($arr)); <br/>归并排序的时间复杂度也是O(nlogn)。原理是:对于两个排序好的数组,分别遍历这两个数组,获取较小的元素插入新的数组中,那么,这么新的数组也会是排序好的。代码如下:
<br/>归并排序的时间复杂度也是O(nlogn)。原理是:对于两个排序好的数组,分别遍历这两个数组,获取较小的元素插入新的数组中,那么,这么新的数组也会是排序好的。代码如下://交换函数function swap(array &$arr,$a,$b){
$temp = $arr[$a]; $arr[$a] = $arr[$b]; $arr[$b] = $temp;
}//归并算法总函数function MergeSort(array &$arr){
$start = 0; $end = count($arr) - 1;
MSort($arr,$start,$end);
}function MSort(array &$arr,$start,$end){ //当子序列长度为1时,$start == $end,不用再分组 if($start < $end){ $mid = floor(($start + $end) / 2); //将 $arr 平分为 $arr[$start - $mid] 和 $arr[$mid+1 - $end] MSort($arr,$start,$mid); //将 $arr[$start - $mid] 归并为有序的$arr[$start - $mid] MSort($arr,$mid + 1,$end); //将 $arr[$mid+1 - $end] 归并为有序的 $arr[$mid+1 - $end] Merge($arr,$start,$mid,$end); //将$arr[$start - $mid]部分和$arr[$mid+1 - $end]部分合并起来成为有序的$arr[$start - $end]
}
}//归并操作function Merge(array &$arr,$start,$mid,$end){
$i = $start; $j=$mid + 1; $k = $start; $temparr = array(); while($i!=$mid+1 && $j!=$end+1)
{ if($arr[$i] >= $arr[$j]){ $temparr[$k++] = $arr[$j++];
} else{ $temparr[$k++] = $arr[$i++];
}
} //将第一个子序列的剩余部分添加到已经排好序的 $temparr 数组中
while($i != $mid+1){ $temparr[$k++] = $arr[$i++];
} //将第二个子序列的剩余部分添加到已经排好序的 $temparr 数组中
while($j != $end+1){ $temparr[$k++] = $arr[$j++];
} for($i=$start; $i<=$end; $i++){ $arr[$i] = $temparr[$i];
}
}$arr = array(9,1,5,8,3,7,4,6,2);
MergeSort($arr);
var_dump($arr);
 Algorithmus zum Ersetzen von Seiten
Algorithmus zum Ersetzen von Seiten
 So öffnen Sie eine PHP-Datei
So öffnen Sie eine PHP-Datei
 Welche Sortiermethoden gibt es?
Welche Sortiermethoden gibt es?
 So entfernen Sie die ersten paar Elemente eines Arrays in PHP
So entfernen Sie die ersten paar Elemente eines Arrays in PHP
 Was tun, wenn die PHP-Deserialisierung fehlschlägt?
Was tun, wenn die PHP-Deserialisierung fehlschlägt?
 So verbinden Sie PHP mit der MSSQL-Datenbank
So verbinden Sie PHP mit der MSSQL-Datenbank
 So verbinden Sie PHP mit der MSSQL-Datenbank
So verbinden Sie PHP mit der MSSQL-Datenbank
 So laden Sie HTML hoch
So laden Sie HTML hoch




