Detaillierte Erklärung der PHP-Heap-Sortierung
Heapsort bezieht sich auf einen Sortieralgorithmus, der eine Datenstruktur wie einen gestapelten Baum (Heap) verwendet. Es handelt sich um eine Art Auswahlsortierung. Sie können die Eigenschaften von Arrays nutzen, um das Element schnell an einem angegebenen Index zu finden. Der Heap ist in einen großen Root-Heap und einen kleinen Root-Heap unterteilt, bei denen es sich um einen vollständigen Binärbaum handelt. Die Anforderung eines großen Root-Heaps besteht darin, dass der Wert jedes Knotens nicht größer ist als der Wert seines übergeordneten Knotens, d. h. A[PARENT[i]] >= A[i]. Bei der nicht absteigenden Sortierung eines Arrays muss ein großer Root-Heap verwendet werden, da gemäß den Anforderungen eines großen Root-Heaps der Maximalwert oben im Heap liegen muss.
Definition von Heap
Wenn in einem vollständigen Binärbaum ein übergeordneter Knoten immer größer oder gleich (kleiner oder gleich) jedem untergeordneten Knoten ist, handelt es sich um einen Big-Top-Heap ( kleiner oberer Haufen).
Heap-Array-Speichermethode
Ein vollständiger Binärbaum eignet sich für die sequentielle Speicherung, sodass ein Array als vollständiger Binärbaum betrachtet werden kann.
Knotennummerierung: Beginnen Sie mit der Wurzel des Baums, von der oberen Ebene zur unteren Ebene, von links nach rechts auf jeder Ebene, nummerieren Sie alle Knoten der Reihe nach, um eine lineare Reihenfolge zu erhalten spiegelt die gesamte binäre Baumstruktur wider.
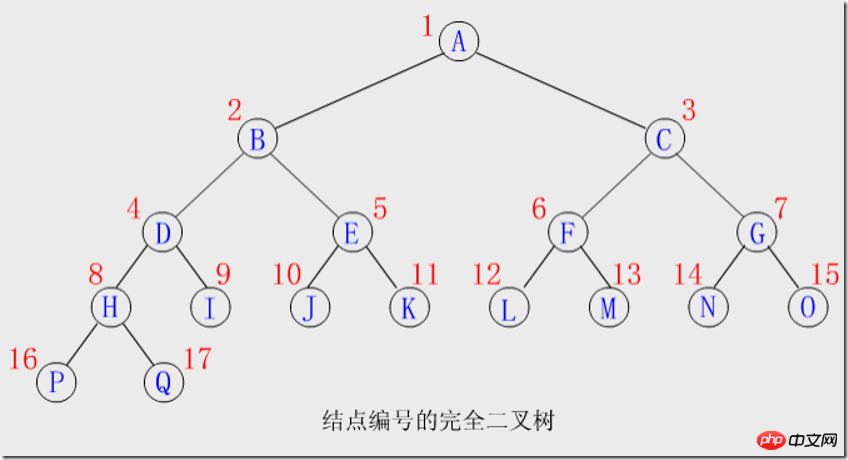
Nummerierungsfunktionen:
Beginnen Sie einfach mit der Nummer eines Knotens Die Knotennummern seiner Eltern, linken und rechten Kinder, Brüder usw. werden abgeleitet. Angenommen, der Knoten mit der Nummer i ist ki (1≤i≤n), dann gilt:
①Wenn i>1, dann ist die übergeordnete Nummer von ki i/2; wenn i=1, dann ist Ki Der Wurzelknoten hat keine übergeordneten Knoten.
②Wenn 2i≤n, dann ist die Zahl des linken Kindes von Ki 2i; andernfalls hat Ki kein linkes Kind, das heißt, Ki muss ein Blatt sein. Daher muss der Knoten mit der Nummer i>n/2 im vollständigen Binärbaum ein Blattknoten sein.
③Wenn 2i+1≤n, dann ist die Zahl des rechten Kindes von Ki 2i+1; andernfalls hat Ki kein richtiges Kind.
Hinweis: Wenn ki (0≤i≤n) den Array-Index erfüllt, sind die möglichen linken und rechten Kinder 2i+1 bzw. 2i+2.
Die Idee der Heap-Sortierung (am Beispiel des Big-Top-Heaps)
Unter Verwendung der Funktion, dass der obere Teil des Heaps das größte Schlüsselwort aufzeichnet, werden in jeder Runde die oberen Elemente von Der Heap wird genommen und in den geordneten Bereich gelegt. So wie bei der Auswahlsortierung in jeder Runde ein Maximalwert ausgewählt und in den geordneten Bereich gelegt wird, kann die Heap-Sortierung als eine Verbesserung der Auswahlsortierung angesehen werden.
Konstruieren Sie die anfängliche Sequenz der zu sortierenden Schlüsselwörter (R0, R1, R2...Rn) in einem großen oberen Heap, dem anfänglichen ungeordneten Bereich
Tauschen Sie das oberste Element R[0] mit dem letzten Element R[n] aus und erhalten Sie einen neuen ungeordneten Bereich (R0, R1, R2,...Rn-1) und den neuen geordneten Bereich ( Rn);
Da die neue Spitze des Heaps R[0] nach dem Austausch möglicherweise die Natur des Heaps verletzt, ist es notwendig, den aktuellen ungeordneten Bereich (R0, R1) zu aktualisieren , R2,...Rn-1) werden an den neuen Heap angepasst.
Wiederholen Sie die Schritte 2 und 3, bis die Anzahl der Elemente im geordneten Bereich n-1 beträgt. Dann ist der gesamte Sortiervorgang abgeschlossen.
Algorithmusanalyse
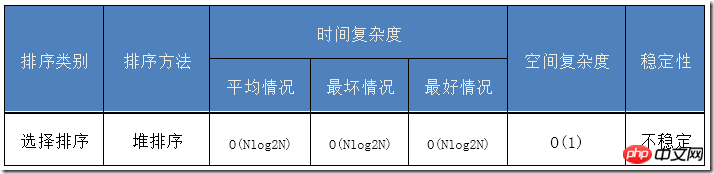
Filteralgorithmus
//Der am schwierigsten zu verstehende Teil
Ziel: Ein vollständiger Binärbaum, in dem alle Teilbäume Heaps sind. Dies bedeutet, dass der einzige Unterschied zwischen diesem Binärbaum und dem Knoten darin besteht, dass er die Heap-Struktur nicht erfüllt. //Sehr wichtig, sehr wichtig, sehr wichtig
Wie unten gezeigt:
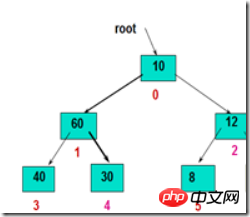
Methode: Erstens Setzen Sie die Wurzel mit den Wurzelknoten ihres linken und rechten Teilbaums und tauschen Sie das größte Element gegen den Wurzelknoten aus. Anschließend wird es entlang des zerstörten Pfads angepasst, bis der Blattknoten erhalten wird.
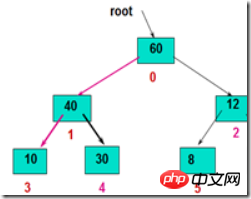
Anwendung: 1. Basierend auf der oben erwähnten Heap-Sortieridee wird in den Schritten 2-3 der ungeordnete Bereich verwendet bei der Anpassung an den Haufen.
2. Initialisieren Sie den Heap
Initialisieren Sie den Heap
vom letzten Nicht-Blattknoten i (i=n/2, n ist der Anzahl der Knoten) Zunächst wird der Binärbaum mit i als Wurzelknoten durch Filterung in einen Heap umgewandelt. Am Beispiel des ersten Bildes lautet die Nummerierungsreihenfolge 8, 7, 6 ... 1.
Die Korrektheit des Screening-Algorithmus ist ab dem letzten Nicht-Blattknoten garantiert, da das Ziel des Screening-Algorithmus ein vollständiger Binärbaum ist, in dem alle Teilbäume Heaps sind.
php实现堆排序:
<?php
//堆排序,对简单排序的改进
function swap(array &$arr,$a,$b)
{
$temp=$arr[$a];
$arr[$a]=$arr[$b];
$arr[$b]=$temp;
}
//调整$arr[$start]的关键字,$arr[$start]、$arr[$start+1]、、、$arr[$end]成为一个大根堆(根节点最大的完全二叉树)
//注意:这里节点s的左右孩子是 2*s +1 和 2*s+2(数组开始下标为0时)
function HeapAdjust(array &$arr $start $end)
{
$temp= $arr[$start];
//沿关键字较大的孩子节点向下筛选
//左右孩子计算 (这里数组的开始下标为0)
//左边孩子 2*$start+1,右边孩子 2*$start+2
for ($j=2*$start+1; $j <=$end; $j=2*$j+1) {
if ($j !=$end &&$arr[$j] <$arr[$j+1]) {
$j++; //转化为右边孩子
}
if ($temp >=$arr[$j]) {
break; //已经满足大根堆
}
//将根节点设置为子节点的较大值
$arr[$start]=$arr[$j];
//继续往下
$start=$j;
}
$arr[$start] =$temp;
}
function HeapSort(array &$arr)
{
$count=count($arr);
//先将数据结构造成大根堆 (由于是完全二叉树,所以这里用floor($count/2-1),下标小于或等于这个数的节点都是有孩子的节点)
for ($i=floor($count /2)-1; $i >=0 ; $i--) {
HeapAdjust($arr,$i,$count);
}
for ($i=$count-1; $i >=0 ; $i--) {
//将堆顶元素与最后一个元素交换,获取到最大元素(交换后的最后一个元素),将最大元素放到数组末尾
swap($arr,0,$i);
//经过交换,将最后一个元素(最大元素)脱离大根堆,并将未经排序的新数($arr[0...$i-1])重新调整为大根堆
HeapAdjust($arr,0,$i-1);
}
}
$arr=array(4,1,5,9);
HeapSort($arr);
vVerwandte Empfehlungen:
PHP-Heap-Sortierung-Implementierungscode
Detaillierte Erklärung der Heap-Sortierung in JavaScript
Detaillierte Erläuterung des PHP-Sortieralgorithmus Heap-Sortierung
Das obige ist der detaillierte Inhalt vonDetaillierte Erklärung der PHP-Heap-Sortierung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1378
1378
 52
52
 PHP 8.4 Installations- und Upgrade-Anleitung für Ubuntu und Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 Installations- und Upgrade-Anleitung für Ubuntu und Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 bringt mehrere neue Funktionen, Sicherheitsverbesserungen und Leistungsverbesserungen mit einer beträchtlichen Menge an veralteten und entfernten Funktionen. In dieser Anleitung wird erklärt, wie Sie PHP 8.4 installieren oder auf PHP 8.4 auf Ubuntu, Debian oder deren Derivaten aktualisieren. Obwohl es möglich ist, PHP aus dem Quellcode zu kompilieren, ist die Installation aus einem APT-Repository wie unten erläutert oft schneller und sicherer, da diese Repositorys in Zukunft die neuesten Fehlerbehebungen und Sicherheitsupdates bereitstellen.
 So richten Sie Visual Studio-Code (VS-Code) für die PHP-Entwicklung ein
Dec 20, 2024 am 11:31 AM
So richten Sie Visual Studio-Code (VS-Code) für die PHP-Entwicklung ein
Dec 20, 2024 am 11:31 AM
Visual Studio Code, auch bekannt als VS Code, ist ein kostenloser Quellcode-Editor – oder eine integrierte Entwicklungsumgebung (IDE) –, die für alle gängigen Betriebssysteme verfügbar ist. Mit einer großen Sammlung von Erweiterungen für viele Programmiersprachen kann VS Code c
 7 PHP-Funktionen, die ich leider vorher nicht kannte
Nov 13, 2024 am 09:42 AM
7 PHP-Funktionen, die ich leider vorher nicht kannte
Nov 13, 2024 am 09:42 AM
Wenn Sie ein erfahrener PHP-Entwickler sind, haben Sie möglicherweise das Gefühl, dass Sie dort waren und dies bereits getan haben. Sie haben eine beträchtliche Anzahl von Anwendungen entwickelt, Millionen von Codezeilen debuggt und eine Reihe von Skripten optimiert, um op zu erreichen
 Wie analysiert und verarbeitet man HTML/XML in PHP?
Feb 07, 2025 am 11:57 AM
Wie analysiert und verarbeitet man HTML/XML in PHP?
Feb 07, 2025 am 11:57 AM
Dieses Tutorial zeigt, wie XML -Dokumente mit PHP effizient verarbeitet werden. XML (Extensible Markup-Sprache) ist eine vielseitige textbasierte Markup-Sprache, die sowohl für die Lesbarkeit des Menschen als auch für die Analyse von Maschinen entwickelt wurde. Es wird üblicherweise für die Datenspeicherung ein verwendet und wird häufig verwendet
 Erklären Sie JSON Web Tokens (JWT) und ihren Anwendungsfall in PHP -APIs.
Apr 05, 2025 am 12:04 AM
Erklären Sie JSON Web Tokens (JWT) und ihren Anwendungsfall in PHP -APIs.
Apr 05, 2025 am 12:04 AM
JWT ist ein offener Standard, der auf JSON basiert und zur sicheren Übertragung von Informationen zwischen Parteien verwendet wird, hauptsächlich für die Identitätsauthentifizierung und den Informationsaustausch. 1. JWT besteht aus drei Teilen: Header, Nutzlast und Signatur. 2. Das Arbeitsprinzip von JWT enthält drei Schritte: Generierung von JWT, Überprüfung von JWT und Parsingnayload. 3. Bei Verwendung von JWT zur Authentifizierung in PHP kann JWT generiert und überprüft werden, und die Funktionen und Berechtigungsinformationen der Benutzer können in die erweiterte Verwendung aufgenommen werden. 4. Häufige Fehler sind Signaturüberprüfungsfehler, Token -Ablauf und übergroße Nutzlast. Zu Debugging -Fähigkeiten gehört die Verwendung von Debugging -Tools und Protokollierung. 5. Leistungsoptimierung und Best Practices umfassen die Verwendung geeigneter Signaturalgorithmen, das Einstellen von Gültigkeitsperioden angemessen.
 PHP -Programm zum Zählen von Vokalen in einer Zeichenfolge
Feb 07, 2025 pm 12:12 PM
PHP -Programm zum Zählen von Vokalen in einer Zeichenfolge
Feb 07, 2025 pm 12:12 PM
Eine Zeichenfolge ist eine Folge von Zeichen, einschließlich Buchstaben, Zahlen und Symbolen. In diesem Tutorial wird lernen, wie Sie die Anzahl der Vokale in einer bestimmten Zeichenfolge in PHP unter Verwendung verschiedener Methoden berechnen. Die Vokale auf Englisch sind a, e, i, o, u und sie können Großbuchstaben oder Kleinbuchstaben sein. Was ist ein Vokal? Vokale sind alphabetische Zeichen, die eine spezifische Aussprache darstellen. Es gibt fünf Vokale in Englisch, einschließlich Großbuchstaben und Kleinbuchstaben: a, e, ich, o, u Beispiel 1 Eingabe: String = "TutorialPoint" Ausgabe: 6 erklären Die Vokale in der String "TutorialPoint" sind u, o, i, a, o, ich. Insgesamt gibt es 6 Yuan
 Erklären Sie die späte statische Bindung in PHP (statisch: :).
Apr 03, 2025 am 12:04 AM
Erklären Sie die späte statische Bindung in PHP (statisch: :).
Apr 03, 2025 am 12:04 AM
Statische Bindung (statisch: :) implementiert die späte statische Bindung (LSB) in PHP, sodass das Aufrufen von Klassen in statischen Kontexten anstatt Klassen zu definieren. 1) Der Analyseprozess wird zur Laufzeit durchgeführt.
 Was sind PHP Magic -Methoden (__construct, __Destruct, __call, __get, __set usw.) und geben Sie Anwendungsfälle an?
Apr 03, 2025 am 12:03 AM
Was sind PHP Magic -Methoden (__construct, __Destruct, __call, __get, __set usw.) und geben Sie Anwendungsfälle an?
Apr 03, 2025 am 12:03 AM
Was sind die magischen Methoden von PHP? Zu den magischen Methoden von PHP gehören: 1. \ _ \ _ Konstrukt, verwendet, um Objekte zu initialisieren; 2. \ _ \ _ Destruct, verwendet zur Reinigung von Ressourcen; 3. \ _ \ _ Call, behandeln Sie nicht existierende Methodenaufrufe; 4. \ _ \ _ GET, Implementieren Sie den dynamischen Attributzugriff; 5. \ _ \ _ Setzen Sie dynamische Attributeinstellungen. Diese Methoden werden in bestimmten Situationen automatisch aufgerufen, wodurch die Code -Flexibilität und -Effizienz verbessert werden.




