 Backend-Entwicklung
Backend-Entwicklung
 Python-Tutorial
Python-Tutorial
 Erweiterte morphologische Verarbeitung der digitalen Bildverarbeitung in Python
Erweiterte morphologische Verarbeitung der digitalen Bildverarbeitung in Python
Erweiterte morphologische Verarbeitung der digitalen Bildverarbeitung in Python
Dieser Artikel stellt hauptsächlich die fortgeschrittene morphologische Verarbeitung der digitalen Bildverarbeitung in Python vor. Jetzt teile ich ihn mit Ihnen und gebe ihn als Referenz. Werfen wir gemeinsam einen Blick darauf
Morphologische Verarbeitung: Zusätzlich zu den grundlegendsten Erweiterungs-, Erosions-, Öffnungs-/Schließoperationen und der Black/White-Hat-Verarbeitung gibt es auch einige fortgeschrittenere Anwendungen, wie z. B. konvexe Hülle und verbundene Regionen Markieren, kleine Bereiche löschen usw.
1. Konvexe Hülle
Die konvexe Hülle bezieht sich auf ein konvexes Polygon, das alle weißen Pixel im Bild enthält. Die Funktion
lautet:
skimage.morphology.convex_hull_image(image)
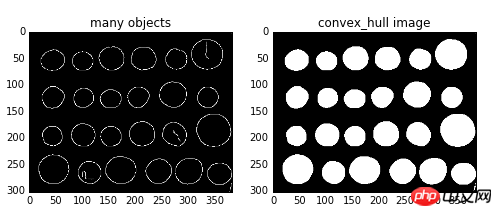
Die Eingabe ist ein Binärbild und die Ausgabe ist ein logisches Binärbild. Punkte innerhalb der konvexen Hülle sind wahr, andernfalls falsch Alle Ziele im Bild als Ganzes, sodass nur ein minimales konvexes Polygon berechnet wird. Wenn das Bild mehrere Zielobjekte enthält und jedes Objekt ein minimales konvexes Polygon berechnen muss, müssen Sie die Funktion convex_hull_object() verwenden.
Funktionsformat:
skimage.morphology.convex_hull_object(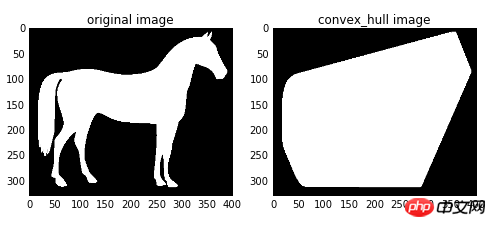 image
image
neighbors=8
)Das Eingabeparameterbild ist ein Binärbild und Nachbarn geben an, ob 4-verbunden oder 8-verbunden verwendet werden soll. Der Standardwert ist 8-verbunden. Beispiel:
import matplotlib.pyplot as plt from skimage import data,color,morphology #生成二值测试图像 img=color.rgb2gray(data.horse()) img=(img<0.5)*1 chull = morphology.convex_hull_image(img) #绘制轮廓 fig, axes = plt.subplots(1,2,figsize=(8,8)) ax0, ax1= axes.ravel() ax0.imshow(img,plt.cm.gray) ax0.set_title('original image') ax1.imshow(chull,plt.cm.gray) ax1.set_title('convex_hull image')
Wenn in einem Binärbild zwei Pixel benachbart sind und den gleichen Wert haben (beide 0 oder 1), dann werden die beiden Pixel als in einem verbundenen Bereich liegend betrachtet. Alle Pixel im selben verbundenen Bereich werden mit demselben Wert markiert. Dieser Vorgang wird als Markierung verbundener Bereiche bezeichnet. Bei der Beurteilung, ob zwei Pixel benachbart sind, verwenden wir normalerweise die Beurteilung nach 4 oder 8 Verbindungen. In einem Bild ist die kleinste Einheit ein Pixel, und jedes Pixel ist von 8 benachbarten Pixeln umgeben. Es gibt zwei übliche Adjazenzbeziehungen: 4-Adjazenz und 8-Adjazenz. 4 grenzt an insgesamt 4 Punkte, nämlich oben, unten, links und rechts, wie im linken Bild unten gezeigt. 8 Es gibt insgesamt 8 benachbarte Punkte, einschließlich der Punkte an diagonalen Positionen, wie in der rechten Abbildung unten dargestellt.
 Im Skimage-Paket verwenden wir die Funktion label() unter dem Measure-Submodul, um die Beschriftung verbundener Bereiche zu implementieren.
Im Skimage-Paket verwenden wir die Funktion label() unter dem Measure-Submodul, um die Beschriftung verbundener Bereiche zu implementieren.
Funktionsformat:
import matplotlib.pyplot as plt from skimage import data,color,morphology,feature #生成二值测试图像 img=color.rgb2gray(data.coins()) #检测canny边缘,得到二值图片 edgs=feature.canny(img, sigma=3, low_threshold=10, high_threshold=50) chull = morphology.convex_hull_object(edgs) #绘制轮廓 fig, axes = plt.subplots(1,2,figsize=(8,8)) ax0, ax1= axes.ravel() ax0.imshow(edgs,plt.cm.gray) ax0.set_title('many objects') ax1.imshow(chull,plt.cm.gray) ax1.set_title('convex_hull image') plt.show()
Das Bild im Parameter stellt das Binärbild dar, das verarbeitet werden muss, Konnektivität stellt den Verbindungsmodus dar, 1 repräsentiert 4 Nachbarschaften, 2 repräsentiert 8 Nachbarschaften. 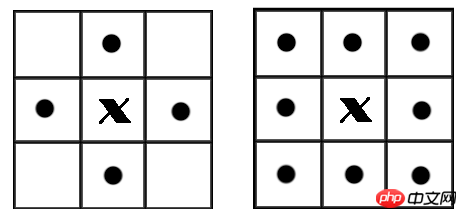
skimage.measure.label(image,connectivity=None)
Wenn Sie jeden verbundenen Bereich separat bearbeiten möchten B. Berechnungsfläche, umschriebenes Rechteck, konvexe Hüllenfläche usw., müssen Sie die Funktion regionprops () des Messsubmoduls aufrufen. Das Format dieser Funktion ist:
import numpy as np import scipy.ndimage as ndi from skimage import measure,color import matplotlib.pyplot as plt #编写一个函数来生成原始二值图像 def microstructure(l=256): n = 5 x, y = np.ogrid[0:l, 0:l] #生成网络 mask = np.zeros((l, l)) generator = np.random.RandomState(1) #随机数种子 points = l * generator.rand(2, n**2) mask[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1 mask = ndi.gaussian_filter(mask, sigma=l/(4.*n)) #高斯滤波 return mask > mask.mean() data = microstructure(l=128)*1 #生成测试图片 labels=measure.label(data,connectivity=2) #8连通区域标记 dst=color.label2rgb(labels) #根据不同的标记显示不同的颜色 print('regions number:',labels.max()+1) #显示连通区域块数(从0开始标记) fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4)) ax1.imshow(data, plt.cm.gray, interpolation='nearest') ax1.axis('off') ax2.imshow(dst,interpolation='nearest') ax2.axis('off') fig.tight_layout() plt.show()
Gibt die Attributliste aller verbundenen Blöcke zurück. Die häufig verwendete Attributliste lautet wie folgt:

3、删除小块区域
有些时候,我们只需要一些大块区域,那些零散的、小块的区域,我们就需要删除掉,则可以使用morphology子模块的remove_small_objects()函数。
函数格式:skimage.morphology.remove_small_objects(ar,min_size=64,connectivity=1,in_place=False)
参数:
ar: 待操作的bool型数组。
min_size: 最小连通区域尺寸,小于该尺寸的都将被删除。默认为64.
connectivity: 邻接模式,1表示4邻接,2表示8邻接
in_place: bool型值,如果为True,表示直接在输入图像中删除小块区域,否则进行复制后再删除。默认为False.
返回删除了小块区域的二值图像。
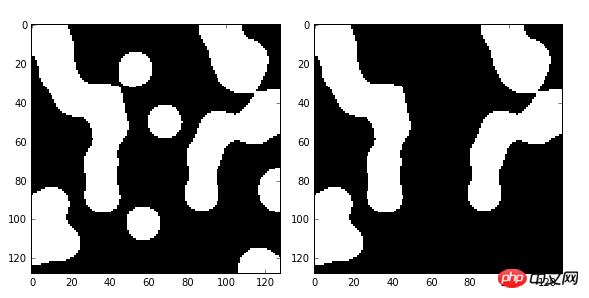
import numpy as np import scipy.ndimage as ndi from skimage import morphology import matplotlib.pyplot as plt #编写一个函数来生成原始二值图像 def microstructure(l=256): n = 5 x, y = np.ogrid[0:l, 0:l] #生成网络 mask = np.zeros((l, l)) generator = np.random.RandomState(1) #随机数种子 points = l * generator.rand(2, n**2) mask[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1 mask = ndi.gaussian_filter(mask, sigma=l/(4.*n)) #高斯滤波 return mask > mask.mean() data = microstructure(l=128) #生成测试图片 dst=morphology.remove_small_objects(data,min_size=300,connectivity=1) fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4)) ax1.imshow(data, plt.cm.gray, interpolation='nearest') ax2.imshow(dst,plt.cm.gray,interpolation='nearest') fig.tight_layout() plt.show()
在此例中,我们将面积小于300的小块区域删除(由1变为0),结果如下图:
4、综合示例:阈值分割+闭运算+连通区域标记+删除小区块+分色显示
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
from skimage import data,filter,segmentation,measure,morphology,color
#加载并裁剪硬币图片
image = data.coins()[50:-50, 50:-50]
thresh =filter.threshold_otsu(image) #阈值分割
bw =morphology.closing(image > thresh, morphology.square(3)) #闭运算
cleared = bw.copy() #复制
segmentation.clear_border(cleared) #清除与边界相连的目标物
label_image =measure.label(cleared) #连通区域标记
borders = np.logical_xor(bw, cleared) #异或
label_image[borders] = -1
image_label_overlay =color.label2rgb(label_image, image=image) #不同标记用不同颜色显示
fig,(ax0,ax1)= plt.subplots(1,2, figsize=(8, 6))
ax0.imshow(cleared,plt.cm.gray)
ax1.imshow(image_label_overlay)
for region in measure.regionprops(label_image): #循环得到每一个连通区域属性集
#忽略小区域
if region.area < 100:
continue
#绘制外包矩形
minr, minc, maxr, maxc = region.bbox
rect = mpatches.Rectangle((minc, minr), maxc - minc, maxr - minr,
fill=False, edgecolor='red', linewidth=2)
ax1.add_patch(rect)
fig.tight_layout()
plt.show()
Das obige ist der detaillierte Inhalt vonErweiterte morphologische Verarbeitung der digitalen Bildverarbeitung in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1382
1382
 52
52
 PHP und Python: Code Beispiele und Vergleich
Apr 15, 2025 am 12:07 AM
PHP und Python: Code Beispiele und Vergleich
Apr 15, 2025 am 12:07 AM
PHP und Python haben ihre eigenen Vor- und Nachteile, und die Wahl hängt von den Projektbedürfnissen und persönlichen Vorlieben ab. 1.PHP eignet sich für eine schnelle Entwicklung und Wartung großer Webanwendungen. 2. Python dominiert das Gebiet der Datenwissenschaft und des maschinellen Lernens.
 Wie ist die GPU -Unterstützung für Pytorch bei CentOS?
Apr 14, 2025 pm 06:48 PM
Wie ist die GPU -Unterstützung für Pytorch bei CentOS?
Apr 14, 2025 pm 06:48 PM
Aktivieren Sie die Pytorch -GPU -Beschleunigung am CentOS -System erfordert die Installation von CUDA-, CUDNN- und GPU -Versionen von Pytorch. Die folgenden Schritte führen Sie durch den Prozess: Cuda und Cudnn Installation Bestimmen Sie die CUDA-Version Kompatibilität: Verwenden Sie den Befehl nvidia-smi, um die von Ihrer NVIDIA-Grafikkarte unterstützte CUDA-Version anzuzeigen. Beispielsweise kann Ihre MX450 -Grafikkarte CUDA11.1 oder höher unterstützen. Download und installieren Sie Cudatoolkit: Besuchen Sie die offizielle Website von Nvidiacudatoolkit und laden Sie die entsprechende Version gemäß der höchsten CUDA -Version herunter und installieren Sie sie, die von Ihrer Grafikkarte unterstützt wird. Installieren Sie die Cudnn -Bibliothek:
 Python gegen JavaScript: Community, Bibliotheken und Ressourcen
Apr 15, 2025 am 12:16 AM
Python gegen JavaScript: Community, Bibliotheken und Ressourcen
Apr 15, 2025 am 12:16 AM
Python und JavaScript haben ihre eigenen Vor- und Nachteile in Bezug auf Gemeinschaft, Bibliotheken und Ressourcen. 1) Die Python-Community ist freundlich und für Anfänger geeignet, aber die Front-End-Entwicklungsressourcen sind nicht so reich wie JavaScript. 2) Python ist leistungsstark in Bibliotheken für Datenwissenschaft und maschinelles Lernen, während JavaScript in Bibliotheken und Front-End-Entwicklungsbibliotheken und Frameworks besser ist. 3) Beide haben reichhaltige Lernressourcen, aber Python eignet sich zum Beginn der offiziellen Dokumente, während JavaScript mit Mdnwebdocs besser ist. Die Wahl sollte auf Projektbedürfnissen und persönlichen Interessen beruhen.
 Detaillierte Erklärung des Docker -Prinzips
Apr 14, 2025 pm 11:57 PM
Detaillierte Erklärung des Docker -Prinzips
Apr 14, 2025 pm 11:57 PM
Docker verwendet Linux -Kernel -Funktionen, um eine effiziente und isolierte Anwendungsumgebung zu bieten. Sein Arbeitsprinzip lautet wie folgt: 1. Der Spiegel wird als schreibgeschützte Vorlage verwendet, die alles enthält, was Sie für die Ausführung der Anwendung benötigen. 2. Das Union File System (UnionFS) stapelt mehrere Dateisysteme, speichert nur die Unterschiede, speichert Platz und beschleunigt. 3. Der Daemon verwaltet die Spiegel und Container, und der Kunde verwendet sie für die Interaktion. 4. Namespaces und CGroups implementieren Container -Isolation und Ressourcenbeschränkungen; 5. Mehrere Netzwerkmodi unterstützen die Containerverbindung. Nur wenn Sie diese Kernkonzepte verstehen, können Sie Docker besser nutzen.
 Miniopen CentOS -Kompatibilität
Apr 14, 2025 pm 05:45 PM
Miniopen CentOS -Kompatibilität
Apr 14, 2025 pm 05:45 PM
Minio-Objektspeicherung: Hochleistungs-Bereitstellung im Rahmen von CentOS System Minio ist ein hochleistungsfähiges, verteiltes Objektspeichersystem, das auf der GO-Sprache entwickelt wurde und mit Amazons3 kompatibel ist. Es unterstützt eine Vielzahl von Kundensprachen, darunter Java, Python, JavaScript und Go. In diesem Artikel wird kurz die Installation und Kompatibilität von Minio zu CentOS -Systemen vorgestellt. CentOS -Versionskompatibilitätsminio wurde in mehreren CentOS -Versionen verifiziert, einschließlich, aber nicht beschränkt auf: CentOS7.9: Bietet einen vollständigen Installationshandbuch für die Clusterkonfiguration, die Umgebungsvorbereitung, die Einstellungen von Konfigurationsdateien, eine Festplattenpartitionierung und Mini
 Wie man eine verteilte Schulung von Pytorch auf CentOS betreibt
Apr 14, 2025 pm 06:36 PM
Wie man eine verteilte Schulung von Pytorch auf CentOS betreibt
Apr 14, 2025 pm 06:36 PM
Pytorch Distributed Training on CentOS -System erfordert die folgenden Schritte: Pytorch -Installation: Die Prämisse ist, dass Python und PIP im CentOS -System installiert sind. Nehmen Sie abhängig von Ihrer CUDA -Version den entsprechenden Installationsbefehl von der offiziellen Pytorch -Website ab. Für CPU-Schulungen können Sie den folgenden Befehl verwenden: PipinstallTorChTorChVisionTorChaudio Wenn Sie GPU-Unterstützung benötigen, stellen Sie sicher, dass die entsprechende Version von CUDA und CUDNN installiert ist und die entsprechende Pytorch-Version für die Installation verwenden. Konfiguration der verteilten Umgebung: Verteiltes Training erfordert in der Regel mehrere Maschinen oder mehrere Maschinen-Mehrfach-GPUs. Ort
 So wählen Sie die Pytorch -Version auf CentOS aus
Apr 14, 2025 pm 06:51 PM
So wählen Sie die Pytorch -Version auf CentOS aus
Apr 14, 2025 pm 06:51 PM
Bei der Installation von PyTorch am CentOS -System müssen Sie die entsprechende Version sorgfältig auswählen und die folgenden Schlüsselfaktoren berücksichtigen: 1. Kompatibilität der Systemumgebung: Betriebssystem: Es wird empfohlen, CentOS7 oder höher zu verwenden. CUDA und CUDNN: Pytorch -Version und CUDA -Version sind eng miteinander verbunden. Beispielsweise erfordert Pytorch1.9.0 CUDA11.1, während Pytorch2.0.1 CUDA11.3 erfordert. Die Cudnn -Version muss auch mit der CUDA -Version übereinstimmen. Bestimmen Sie vor der Auswahl der Pytorch -Version unbedingt, dass kompatible CUDA- und CUDNN -Versionen installiert wurden. Python -Version: Pytorch Official Branch
 So installieren Sie Nginx in CentOS
Apr 14, 2025 pm 08:06 PM
So installieren Sie Nginx in CentOS
Apr 14, 2025 pm 08:06 PM
Die Installation von CentOS-Installationen erfordert die folgenden Schritte: Installieren von Abhängigkeiten wie Entwicklungstools, PCRE-Devel und OpenSSL-Devel. Laden Sie das Nginx -Quellcode -Paket herunter, entpacken Sie es, kompilieren Sie es und installieren Sie es und geben Sie den Installationspfad als/usr/local/nginx an. Erstellen Sie NGINX -Benutzer und Benutzergruppen und setzen Sie Berechtigungen. Ändern Sie die Konfigurationsdatei nginx.conf und konfigurieren Sie den Hörport und den Domänennamen/die IP -Adresse. Starten Sie den Nginx -Dienst. Häufige Fehler müssen beachtet werden, z. B. Abhängigkeitsprobleme, Portkonflikte und Konfigurationsdateifehler. Die Leistungsoptimierung muss entsprechend der spezifischen Situation angepasst werden, z. B. das Einschalten des Cache und die Anpassung der Anzahl der Arbeitsprozesse.



