
Dieser Artikel stellt hauptsächlich Beispiele für die Verwendung von Lasso-Regressions- und Ridge-Regressionsalgorithmen vor. Jetzt kann ich ihn mit Ihnen teilen.
Es gibt auch Einige reguläre Methoden können den Einfluss von Koeffizienten auf die Ausgabeergebnisse von Regressionsalgorithmen begrenzen. Die beiden am häufigsten verwendeten Regularisierungsmethoden sind Lasso-Regression und Ridge-Regression.
Die Lasso-Regressions- und Ridge-Regressions-Algorithmen sind dem herkömmlichen linearen Regressionsalgorithmus sehr ähnlich. Der einzige Unterschied besteht darin, dass der Formel ein regulärer Term hinzugefügt wird, um die Steigung (oder Nettosteigung) zu begrenzen. Der Hauptgrund dafür besteht darin, den Einfluss des Merkmals auf die abhängige Variable zu begrenzen, was durch Hinzufügen einer Verlustfunktion erreicht wird, die von der Steigung A abhängt.
Fügen Sie für den Lasso-Regressionsalgorithmus ein Element zur Verlustfunktion hinzu: ein gegebenes Vielfaches der Steigung A. Wir verwenden die logischen Operationen von TensorFlow, jedoch ohne die mit diesen Operationen verbundenen Verläufe. Stattdessen verwenden wir eine kontinuierliche Schätzung einer Schrittfunktion, auch kontinuierliche Schrittfunktion genannt, die an einem Grenzpunkt springt und sich ausdehnt. Sie werden gleich sehen, wie Sie den Lasso-Regressionsalgorithmus verwenden.
Fügen Sie für den Ridge-Regressionsalgorithmus eine L2-Norm hinzu, bei der es sich um die L2-Regularisierung des Steigungskoeffizienten handelt.
# LASSO and Ridge Regression
# lasso回归和岭回归
#
# This function shows how to use TensorFlow to solve LASSO or
# Ridge regression for
# y = Ax + b
#
# We will use the iris data, specifically:
# y = Sepal Length
# x = Petal Width
# import required libraries
import matplotlib.pyplot as plt
import sys
import numpy as np
import tensorflow as tf
from sklearn import datasets
from tensorflow.python.framework import ops
# Specify 'Ridge' or 'LASSO'
regression_type = 'LASSO'
# clear out old graph
ops.reset_default_graph()
# Create graph
sess = tf.Session()
###
# Load iris data
###
# iris.data = [(Sepal Length, Sepal Width, Petal Length, Petal Width)]
iris = datasets.load_iris()
x_vals = np.array([x[3] for x in iris.data])
y_vals = np.array([y[0] for y in iris.data])
###
# Model Parameters
###
# Declare batch size
batch_size = 50
# Initialize placeholders
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
# make results reproducible
seed = 13
np.random.seed(seed)
tf.set_random_seed(seed)
# Create variables for linear regression
A = tf.Variable(tf.random_normal(shape=[1,1]))
b = tf.Variable(tf.random_normal(shape=[1,1]))
# Declare model operations
model_output = tf.add(tf.matmul(x_data, A), b)
###
# Loss Functions
###
# Select appropriate loss function based on regression type
if regression_type == 'LASSO':
# Declare Lasso loss function
# 增加损失函数,其为改良过的连续阶跃函数,lasso回归的截止点设为0.9。
# 这意味着限制斜率系数不超过0.9
# Lasso Loss = L2_Loss + heavyside_step,
# Where heavyside_step ~ 0 if A < constant, otherwise ~ 99
lasso_param = tf.constant(0.9)
heavyside_step = tf.truep(1., tf.add(1., tf.exp(tf.multiply(-50., tf.subtract(A, lasso_param)))))
regularization_param = tf.multiply(heavyside_step, 99.)
loss = tf.add(tf.reduce_mean(tf.square(y_target - model_output)), regularization_param)
elif regression_type == 'Ridge':
# Declare the Ridge loss function
# Ridge loss = L2_loss + L2 norm of slope
ridge_param = tf.constant(1.)
ridge_loss = tf.reduce_mean(tf.square(A))
loss = tf.expand_dims(tf.add(tf.reduce_mean(tf.square(y_target - model_output)), tf.multiply(ridge_param, ridge_loss)), 0)
else:
print('Invalid regression_type parameter value',file=sys.stderr)
###
# Optimizer
###
# Declare optimizer
my_opt = tf.train.GradientDescentOptimizer(0.001)
train_step = my_opt.minimize(loss)
###
# Run regression
###
# Initialize variables
init = tf.global_variables_initializer()
sess.run(init)
# Training loop
loss_vec = []
for i in range(1500):
rand_index = np.random.choice(len(x_vals), size=batch_size)
rand_x = np.transpose([x_vals[rand_index]])
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
loss_vec.append(temp_loss[0])
if (i+1)%300==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b)))
print('Loss = ' + str(temp_loss))
print('\n')
###
# Extract regression results
###
# Get the optimal coefficients
[slope] = sess.run(A)
[y_intercept] = sess.run(b)
# Get best fit line
best_fit = []
for i in x_vals:
best_fit.append(slope*i+y_intercept)
###
# Plot results
###
# Plot regression line against data points
plt.plot(x_vals, y_vals, 'o', label='Data Points')
plt.plot(x_vals, best_fit, 'r-', label='Best fit line', linewidth=3)
plt.legend(loc='upper left')
plt.title('Sepal Length vs Pedal Width')
plt.xlabel('Pedal Width')
plt.ylabel('Sepal Length')
plt.show()
# Plot loss over time
plt.plot(loss_vec, 'k-')
plt.title(regression_type + ' Loss per Generation')
plt.xlabel('Generation')
plt.ylabel('Loss')
plt.show()Ausgabeergebnis:
Schritt #300 A = [[ 0,77170753]] b = [[ 1,82499862]]
Verlust = [[ 10,26473045]]
Schritt #600 A = [[ 0,75908542]] b = [[ 3,2220633]]
Verlust = [[ 3,06292033]]
Schritt #900 A = [[ 0,74843585] ] b = [[ 3,9975822]]
Verlust = [[ 1,23220456]]
Schritt #1200 A = [[ 0,73752165]] b = [[ 4,42974091]]
Verlust = [[ 0,57872057]]
Schritt #1500 A = [[ 0,72942668]] b = [[ 4,67253113]]
Verlust = [[ 0,40874988]]
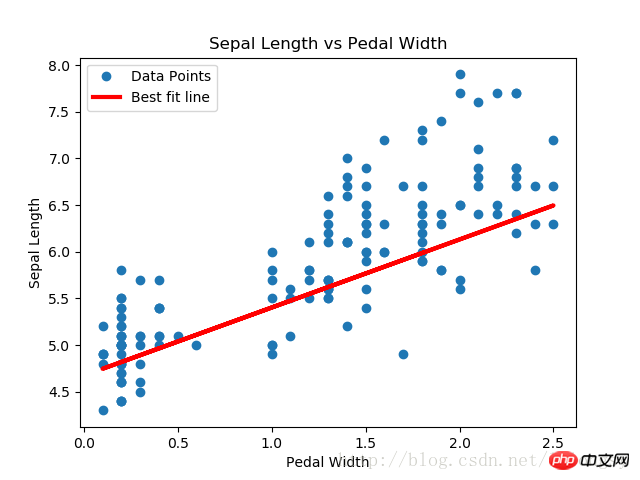
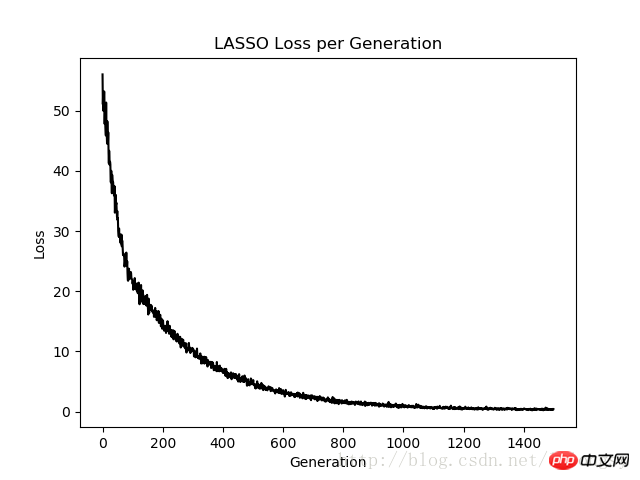
Der Lasso-Regressionsalgorithmus wird durch Hinzufügen einer kontinuierlichen Schrittfunktion basierend auf der standardmäßigen linearen Regressionsschätzung implementiert. Aufgrund der Steigung der Schrittfunktion müssen wir auf die Schrittgröße achten, da eine zu große Schrittgröße letztendlich zu Nichtkonvergenz führt.
Verwandte Empfehlungen:
Beispiel für die Verwendung von TensorFlow zur Implementierung des Deming-Regressionsalgorithmus
Das obige ist der detaillierte Inhalt vonBeispiele für die Implementierung von Lasso-Regressions- und Ridge-Regressionsalgorithmen mit TensorFlow. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




