Rekursion auf Basis der PHP-Datenstruktur

Dieser Artikel stellt hauptsächlich die Rekursion auf der Grundlage der PHP-Datenstruktur vor. Sie hat einen bestimmten Referenzwert. Jetzt können Freunde in Not darauf verweisen.

Was ist Rekursion?

Wie bereits erwähnt, ist Rekursion eine Lösung, die große Probleme in kleine zerlegt. Im Allgemeinen wird Rekursion als Aufruf der Funktion selbst bezeichnet. Es mag seltsam klingen, das zu sagen, aber tatsächlich muss sich die Funktion bei der Rekursion selbst aufrufen.

Eine Kastanie

Zum Beispiel kennen wir alle in der Mathematik den Begriff „Fakultät“. Die Fakultät von 5 ist beispielsweise 5*4*3*2*1.

• 5! = 5 * 4!

• 4! = 4 * 3!

• 3! = 3 * 2!

• 2! = 2 * 1!

• 1! = 1 * 0!

• 0! = 1

Wir können die Regel zum Ermitteln der Fakultät von n zusammenfassen, das heißt n! = n * (n -1) !

Dies spiegelt die Rekursion wider. Daraus können Sie ersehen, dass wir die Fakultät von 5 Schritt für Schritt in ein weiteres kleines Problem umgewandelt haben.

Eigenschaften rekursiver Algorithmen

• Jedem rekursiven Aufruf muss ein kleines Teilproblem zugrunde liegen. Beispielsweise ist die Fakultät 5 die Fakultät 5 mal 4.

• Rekursion muss einen Basisfall haben. Der Basisfall von „Fakultät“ ist beispielsweise 0. Wenn die Bedingung 0 ist, stoppt die Rekursion.

• Vermeiden Sie Schleifenaufrufe während der Rekursion, da der Computer sonst am Ende einen Stapelüberlauffehler anzeigt.

function factorial(int $n): int
{
    if ($n = 0) {
        return 1;
    }
    
    return $n * factorial($n - 1);
}

Wenn wir uns den obigen Code ansehen, können wir sehen, dass wir eine Grundbedingung für die Lösung des Fakultätsproblems haben, nämlich dass wir 1 zurückgeben, wenn n 0 ist. Wenn diese Bedingung nicht erfüllt ist, geben wir n mal factorial(n) zurück, was der ersten und dritten rekursiven Eigenschaft entspricht. Wir vermeiden Aufrufschleifen, weil wir jeden rekursiven Aufruf in ein kleineres Teilproblem des größeren Problems aufteilen. Die obige Algorithmusidee kann ausgedrückt werden als:

Rekursion vs. Iteration

Wir können auch die iterative Methode verwenden, um den obigen rekursiven Code zu implementieren

function factorial(int $n): int
{
    $result = 1;
    
    for ($i = $n; $i > 0; $i--) {
        $result*= $n;
    }
    
    return $result;
}

Wenn ein Problem auftritt Es kann sehr einfach sein, Iteration zur Lösung zu verwenden. Warum verwenden wir Rekursion?

Rekursion wird verwendet, um komplexere Probleme zu lösen. Nicht alle Probleme können einfach durch Iteration gelöst werden. Bei der Rekursion werden Funktionsaufrufe zur Verwaltung des Aufrufstapels verwendet. Daher benötigt die Rekursion mehr Zeit und Speicher als die Iteration. Darüber hinaus erhalten wir bei der Iteration bei jedem Schritt ein Ergebnis, bei der Rekursion müssen wir jedoch warten, bis die Ausführung des Basisfalls abgeschlossen ist, bevor wir ein Ergebnis erhalten. Wenn wir uns das obige Beispiel ansehen, stellen wir fest, dass wir im rekursiven Algorithmus keine Variablen oder Deklarationen zum Speichern der Ergebnisse haben, während wir im iterativen Algorithmus jedes Mal $result verwenden, um die zurückgegebenen Ergebnisse zu speichern.

Fibonacci-Folge

In der Mathematik ist die Fibonacci-Folge eine spezielle Folge von ganzen Zahlen. Jede Zahl in der Folge wird durch die Summe zweier anderer Zahlen erzeugt. Die Regeln lauten wie folgt:

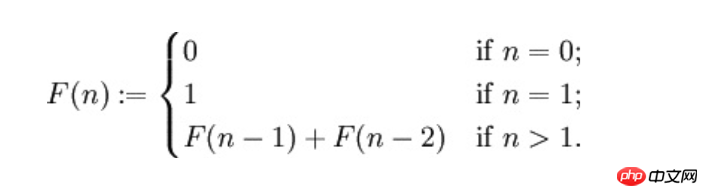
function fibonacci($n)
{
    if ($n == 0) {
        return 0;
    }
    
    if ($n == 1) {
        return 1;
    }
    
    return fibonacci($n - 1) + fibonacci($ - 2);
}

Größter gemeinsamer Faktor

Ein weiteres häufiges Problem bei der Verwendung rekursiver Algorithmen besteht darin, den größten gemeinsamen Faktor zweier Zahlen zu finden.

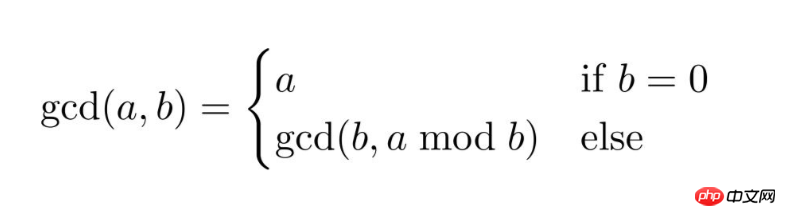
function gcd(int $a, int $b)
{
    if ($b == 0) {
        return $a;
    }
    
    return gcd($b, $a % $b);
}

Rekursionstyp

• Lineare Rekursion

in jedem rekursiven Aufruf , the Die Funktion ruft sich nur einmal auf, was als lineare Rekursion bezeichnet wird.

• Biäre Rekursion

Bei der binären Rekursion ruft sich jeder rekursive Aufruf der Funktion zweimal selbst auf. Der Algorithmus zum Lösen der Fibonacci-Folge ist eine binäre Rekursion. Darüber hinaus verwenden die binäre Suche, der Divide-and-Conquer-Algorithmus, die Zusammenführungssortierung usw. auch die binäre Rekursion.

• Tail-Rekursion

Wenn eine rekursive Rückkehr keine Warteoperationen hat, spricht man von Tail-Rekursion. Im Fibonacci-Algorithmus muss der Rückgabewert mit dem Rückgabewert der vorherigen Rekursion multipliziert werden, sodass er nicht schwanzrekursiv ist, und der Algorithmus zum Lösen des größten gemeinsamen Faktors ist schwanzrekursiv. Die Schwanzrekursion ist eine Form der linearen Rekursion.

• Gegenseitige Rekursion

Zum Beispiel ruft A() bei jedem rekursiven Aufruf B() auf, B() ruft A() auf, Eine solche Rekursion wird gegenseitige Rekursion genannt.

• Verschachtelte Rekursion

Wenn eine rekursive Funktion sich selbst rekursiv als Parameter aufruft, spricht man von verschachtelter Rekursion. Ein häufiges Beispiel ist die Ackerman-Funktion, siehe den folgenden Ausdruck.

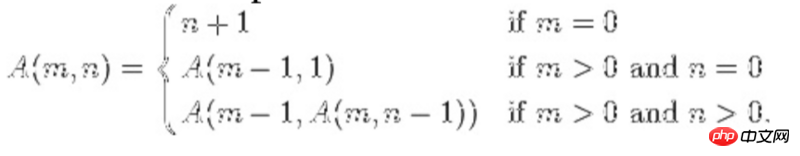
Wenn Sie sich die letzte Zeile ansehen, können Sie sehen, dass der zweite Parameter die rekursive Funktion selbst ist.

Nächster Abschnitt

Im nächsten Artikel wird die Rekursion verwendet, um einige Probleme zu lösen, die bei der tatsächlichen Entwicklung auftreten, z. B. das Erstellen von N-Level-Klassifizierungen, das Erstellen verschachtelter Kommentare, das Durchlaufen von Verzeichnisdateien usw. .

Das Obige ist der gesamte Inhalt dieses Artikels. Ich hoffe, dass er für das Studium aller hilfreich ist. Weitere verwandte Inhalte finden Sie auf der chinesischen PHP-Website.

Verwandte Empfehlungen:

So erhalten Sie die echte IP-Adresse des Clients in PHP

So verwenden Sie Elasticsearch in PHP

Das obige ist der detaillierte Inhalt vonRekursion auf Basis der PHP-Datenstruktur. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!