In diesem Artikel wird hauptsächlich die JS-Implementierung der Heap-Sortierung vorgestellt, die einen gewissen Referenzwert hat. Freunde in Not können sich auf
Vorkenntnisse über Heap beziehen 🎜>
Der Heap ist ein vollständiger Binärbaum.
-
Vollständiger Binärbaum: Mit Ausnahme der letzten Schicht des Binärbaums erreicht die Anzahl der Knoten in anderen Schichten ihr Maximum und alle Knoten in der letzten Schicht sind auf der linken Seite konzentriert (Wenn die Knoten auf der linken Seite voll sind, können Knoten nur auf der rechten Seite fehlen).
-
Big Top Heap: Der Wurzelknoten ist der Maximalwert, und der Wert jedes Knotens ist größer oder gleich dem Wert seines untergeordneten Knotens.
-
Kleiner oberer Heap: Der Wurzelknoten ist der Mindestwert, und der Wert jedes Knotens ist kleiner oder gleich dem Wert seines untergeordneten Knotens.
-
Heap-Speicher: Der Heap wird durch ein Array implementiert, was einer Durchquerung eines Binärbaums in Ebenenreihenfolge entspricht. Wie unten gezeigt:
Für Knoten i, seine untergeordneten Knoten Die Punkte sind 2
i+1 und 2
i+2.
Heap-Sortieralgorithmus
Jetzt müssen wir den obigen Binärbaum in aufsteigender Reihenfolge sortieren, die in drei Schritte unterteilt ist: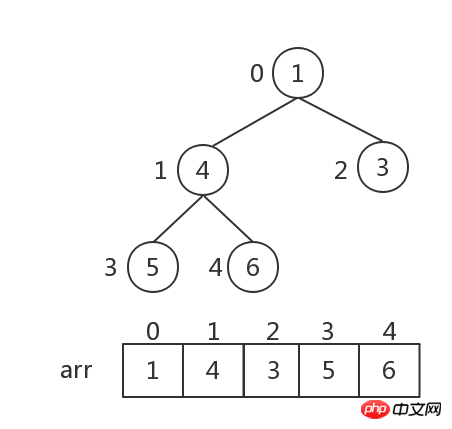 
Konvertieren Sie den anfänglichen Binärbaum in einen großen oberen Heap (Heapify). Zu diesem Zeitpunkt hat der Wurzelknoten den Maximalwert und wird mit dem letzten Knoten ausgetauscht.
-
Mit Ausnahme des letzten Knotens wird der neue Heap, der aus den verbleibenden Knoten besteht, in einen großen oberen Heap umgewandelt. Zu diesem Zeitpunkt ist der Wurzelknoten der submaximale Wert mit dem letzten Knoten ausgetauscht.
-
Wiederholen Sie Schritt 2, bis die Anzahl der Elemente im Heap 1 beträgt (oder die Länge des entsprechenden Arrays 1 beträgt) und die Sortierung abgeschlossen ist.
-
Der Prozess wird unten im Detail dargestellt:
Schritt 1:
Initialisieren Sie den großen oberen Heap, wählen Sie zuerst den letzten Nicht-Blattknoten aus ( Wir müssen nur die Größenbeziehung zwischen dem übergeordneten Knoten und dem untergeordneten Knoten anpassen. Die Größenbeziehung zwischen den Blattknoten muss nicht angepasst werden. Angenommen, das Array ist arr, dann lautet der Index des ersten Nicht-Blattknotens: i = Math.floor(arr.length/2 - 1) = 1, was der Zahl 4 entspricht, wie im gepunkteten Kästchen in der Abbildung dargestellt Finden Sie drei Zahlen. Der Maximalwert wird mit dem übergeordneten Knoten ausgetauscht.
Dann wird der Index i um 1 dekrementiert (d. h. beginnend mit dem ersten Nicht-Blattknoten, alle Nicht-Blattknoten von rechts nach links durchlaufend). von unten nach oben). Jede weitere Anpassung ist gleich: Finden Sie den Maximalwert zwischen den übergeordneten und untergeordneten Knoten und führen Sie einen Austausch durch.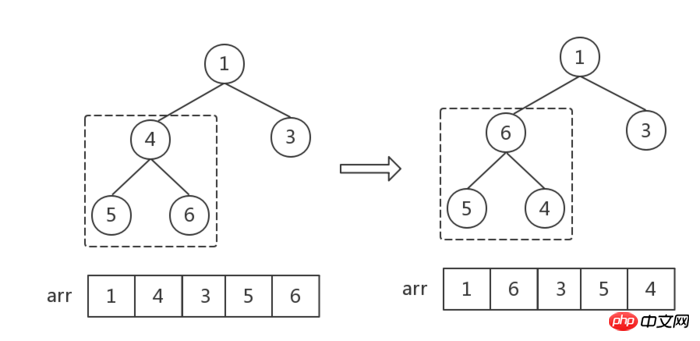 
Nachdem in diesem Schritt die Zahlen 6 und 1 ausgetauscht wurden, ist die Reihenfolge des aus den Zahlen [1,5,4] zusammengesetzten Haufens falsch und ein Anpassungsschritt erforderlich ist erforderlich. Daher ist es wichtig zu beachten, dass Sie bei jeder Anpassung an einem Nicht-Blattknoten darauf achten müssen, ob sich dies auf die Sub-Heap-Reihenfolge auswirkt!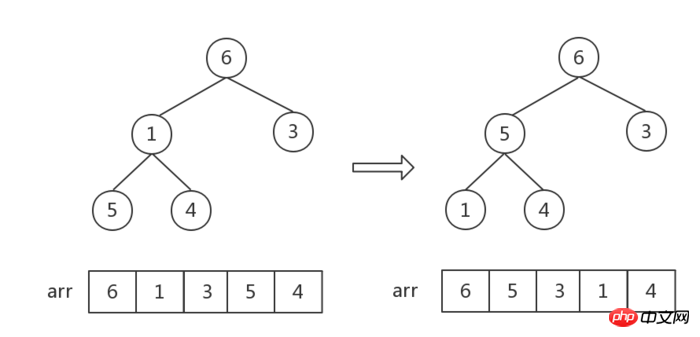 
Nach dieser Anpassung hat der Wurzelknoten den Maximalwert und bildet einen großen oberen Heap, und der Wurzelknoten wird mit dem letzten Knoten ausgetauscht.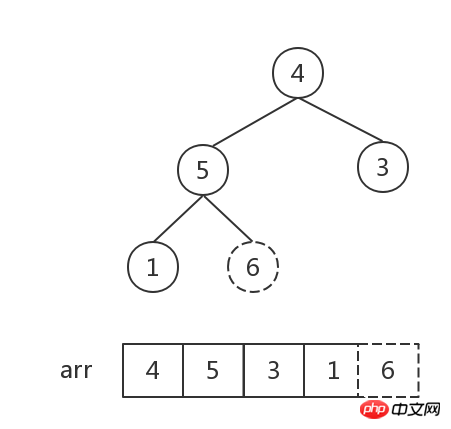 
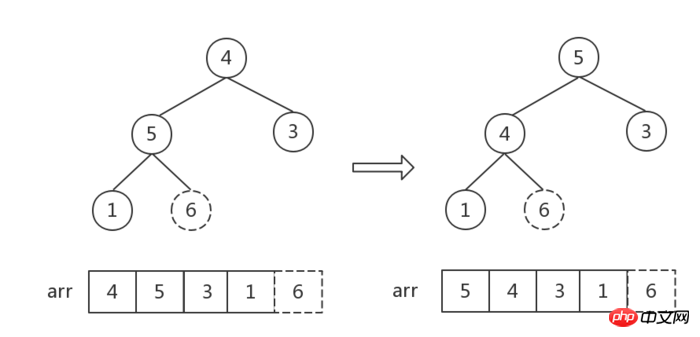
Schritt 2:
Bilden Sie mit Ausnahme des aktuell letzten Knotens 6 (d. h. des Maximalwerts) einen neuen Heap der verbleibenden Knoten [4,5,3,1] und konvertieren Sie ihn in ein großer oberer Heap ( Achten Sie auf die Beobachtung. Zu diesem Zeitpunkt erfüllen alle anderen Knoten außer dem Wurzelknoten die Eigenschaften eines großen oberen Heaps, sodass Sie mit der Anpassung vom Wurzelknoten 4 aus beginnen können, dh die Position finden, an der sich 4 befindet sollte sein).
Schritt 3: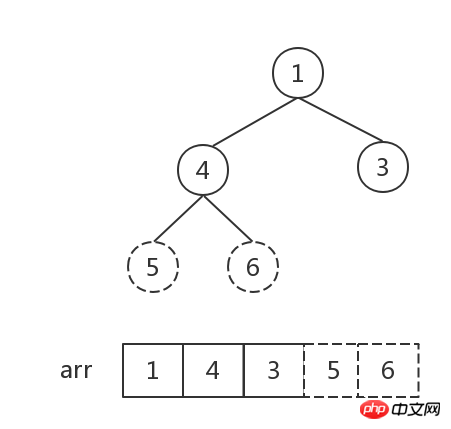 
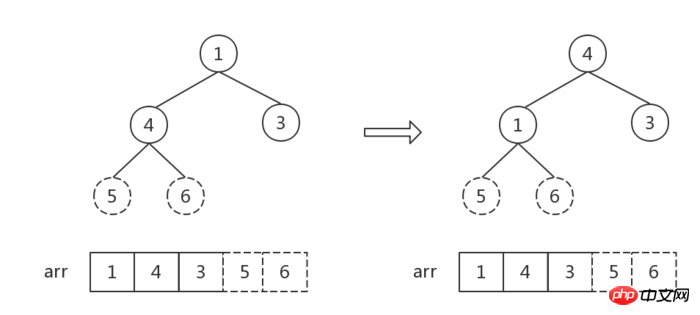
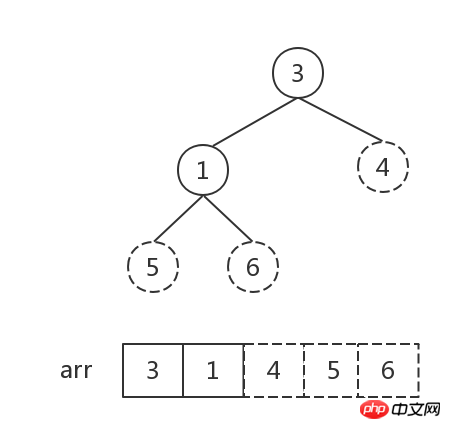
Als nächstes wiederholen Sie Schritt 2, bis die Anzahl erreicht ist Elemente im Heap ist 1:
Die Anzahl der Elemente im Heap ist 1, Sortieren Finish.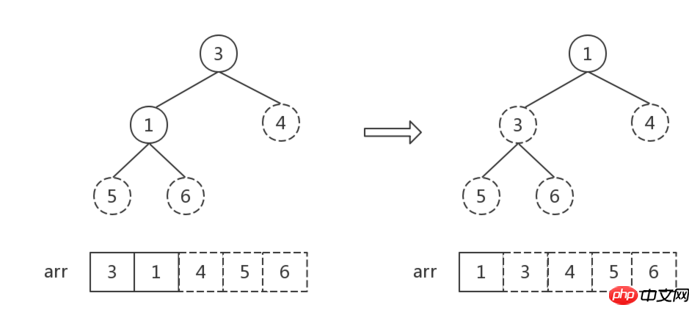 
JavaScript-Implementierung
// 交换两个节点
function swap(A, i, j) {
let temp = A[i];
A[i] = A[j];
A[j] = temp;
}
// 将 i 结点以下的堆整理为大顶堆，注意这一步实现的基础实际上是：
// 假设 结点 i 以下的子堆已经是一个大顶堆，adjustheap 函数实现的
// 功能是实际上是：找到 结点 i 在包括结点 i 的堆中的正确位置。后面
// 将写一个 for 循环，从第一个非叶子结点开始，对每一个非叶子结点
// 都执行 adjustheap 操作，所以就满足了结点 i 以下的子堆已经是一大
//顶堆
function adjustHeap(A, i, length) {
let temp = A[i]; // 当前父节点
// j<length function>=0; i--) {
adjustHeap(A, i, A.length);
}
// 排序，每一次for循环找出一个当前最大值，数组长度减一
for(let i = Math.floor(A.length-1); i>0; i--) {
swap(A, 0, i); // 根节点与最后一个节点交换
adjustHeap(A, 0, i); // 从根节点开始调整，并且最后一个结点已经为当
// 前最大值，不需要再参与比较，所以第三个参数
// 为 i，即比较到最后一个结点前一个即可
}
}
let Arr = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];
heapSort(Arr);
alert(Arr);</length>Nach dem Login kopieren
Programmhinweise: Organisieren Sie den Heap unter Knoten i in einen großen oberen Heap. Beachten Sie, dass die Grundlage dieses Schritts tatsächlich ist: Angenommen, der Unter-Heap unter Knoten i ist bereits groß Oberer Heap Auf dem oberen Heap besteht die von der Funktion „adjustHeap“ implementierte Funktion tatsächlich darin, die korrekte Position des Knotens i im Heap einschließlich Knoten i zu finden. Wenn später der erste Heap ausgeführt wird, wird eine for-Schleife in heapSort geschrieben. Beginnend mit dem ersten Nicht-Blattknoten wird die AdjustHeap-Operation auf jedem Nicht-Blattknoten ausgeführt, sodass sichergestellt ist, dass in jedem AdjustHeap der Knoten der Unterknoten ist. Der Heap unter i ist bereits ein großer Top-Heap.
Komplexitätsanalyse: Die Funktion „adjustHeap“ entspricht dem Durchlaufen nur eines Knotens für jede Ebene des Heaps, da
die Tiefe eines vollständigen Binärbaums mit n Knoten [log2n] + 1 beträgt, sodass die Funktion von „adjustHeap“ beträgt Die Komplexität beträgt O(logn) und die äußere Schleife hat f(n)-mal, sodass die endgültige Komplexität O(nlogn) ist.
Heap-Anwendung
Heap wird hauptsächlich zur Implementierung der Prioritätswarteschlange verwendet. Das Folgende ist ein Anwendungsbeispiel für die Prioritätswarteschlange:
Das Betriebssystem dynamisch Wählt die Ausführung der obersten Mission mit Priorität aus.
Wählen Sie in einem statischen Problem die obersten M-Namen aus N Elementen aus. Die Komplexität der Verwendung der Sortierung: O(NlogN) und die Komplexität der Verwendung der Prioritätswarteschlange: O(NlogM).
Die unterschiedlichen Komplexitäten der Implementierung von Prioritätswarteschlangen mit gewöhnlichen Arrays, sequentiellen Arrays und Heaps sind wie folgt:
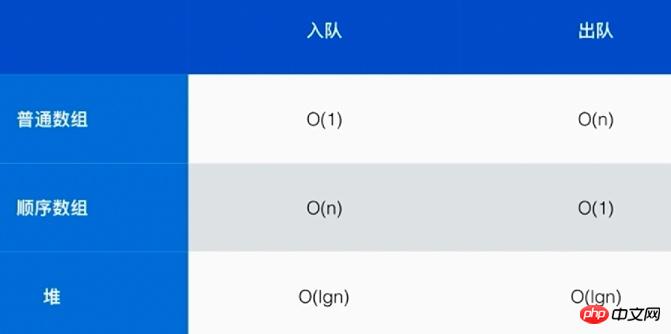
Verwenden Sie Heaps zur Implementierung Prioritätswarteschlangen können die Komplexität des Beitretens und Entfernens aus der Warteschlange sehr gering machen.
Das Obige ist der gesamte Inhalt dieses Artikels. Ich hoffe, er wird für das Studium aller hilfreich sein. Weitere verwandte Inhalte finden Sie auf der chinesischen PHP-Website.
Verwandte Empfehlungen:
JS implementiert Zusammenführungssortierung
JS implementiert Hill-Sortierung
Das obige ist der detaillierte Inhalt vonJS implementiert Heap-Sortierung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
