
Problem
GegebeneN Artikel und ein Rucksack mit Kapazität V, Artikel Das Volumen von i ist wi und sein Wert ist ci.
(Nur einer von jedem Artikel)
F: Wie wähle ich die Artikel aus, die in den Rucksack gesteckt werden sollen, damit der Gesamtwert der Artikel im Rucksack maximal ist?
Bei jedem Gegenstand haben wir nur zwei Möglichkeiten: einlegen oder nicht einlegen. Jeder Gegenstand kann nur einmal eingelegt werden.
Lassen Sie uns die gleiche Idee wie zuvor ausprobieren
Angenommen, dass nur noch das letzte Element übrig ist, haben wir zwei Möglichkeiten
1. Wenn der verbleibende Platz ausreicht, entscheiden Sie sich, es einzufügen
2. Wenn der verbleibende Platz nicht ausreicht, legen Sie
nicht hinein, damit wir zwei optimale Unterkonstruktionen haben:
1 Die optimale Art, i-1-Gegenstände in einen Rucksack mit einem Fassungsvermögen von V zu stecken
2. Die optimale Wahl, um i-1-Gegenstände in einen Rucksack mit der Kapazität V-w[i] zu packen
Zusammenfassend ist es also:
i Die optimale Wahl zum Verstauen von Gegenständen in einem Rucksack mit Kapazität V:
max (die optimale Wahl zum Verstauen von i-1-Gegenständen in einem Rucksack mit Kapazität V und zum Unterbringen von i-1-Gegenständen in einem Rucksack mit Kapazität V-w[ i] – Die optimale Wahl von 1 Element + c[i])
Wir verwenden f[i][v], um den Maximalwert darzustellen, der durch Einfügen der ersten i Elemente in a erhalten werden kann Rucksack mit Kapazität v .
Definieren Sie den Zustand mithilfe von Unterproblemen:
Die Zustandsübergangsgleichung lautet: f[i] [v] = max{f[i-1] [v],f[i-1] [ v-w[i]]+c[i]}.
Nehmen wir zunächst an
Die Gesamtkapazität des Rucksacks beträgt V = 12
Das Kapazitätsarray der Gegenstände ist w = [4, 6, 2, 2, 5, 1]
Das Wertearray ist c = [8, 10, 6, 3, 7, 2]
f(i,v) = 0 (i
f(i,v) = c[0] (i==1, v>=p[0]);
f(i,v) = f(i-1,v) (i>1, v
f(i,v) = max(f(i-1,v), f(i-1,v-w[i-1])+c[i -1])(i> ;1, v>=w[i-1])
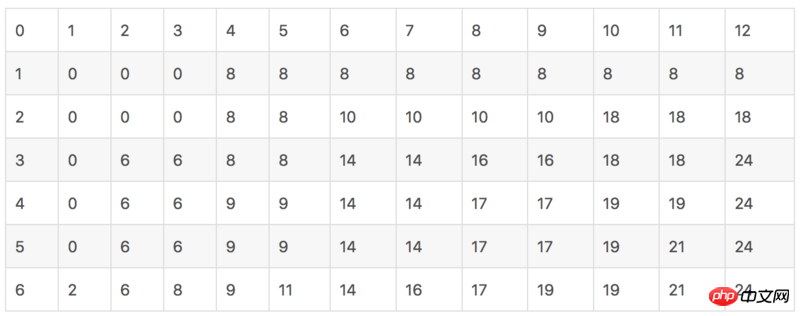
Wir speichern die vorherigen Daten von links jedes Mal nach rechts
Wenn Sie von oben nach unten gehen, speichern Sie die Daten der vorherigen Zeile
Im Allgemeinen müssen wir also nur eine Datenzeile speichern, die Raumkomplexität beträgt O(V)
Die Zeit Die Komplexität ist O(N*V), die Raumkomplexität ist O(V);
Wenn wir jedoch die ursprüngliche rekursive Methode verwenden, also die Permutations- und Kombinationsmethode, beträgt die Zeitkomplexität O(2 ^N) ;
JS zur Implementierung des dynamischen Programmier-Rucksack-Algorithmus
Beispielanalyse für dynamische Programmierung mit erweitertem JavaScript-Algorithmus
Das obige ist der detaillierte Inhalt vonJS-Tutorial – Rucksackkapazitätsproblem des dynamischen Programmieralgorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




