Der Inhalt dieses Artikels befasst sich mit der Verwendung von Canvas zum Zeichnen glatter Kurven. Ich hoffe, dass er für Sie hilfreich ist.
Hintergrundzusammenfassung
Ich glaube, dass jeder beim Erlernen von Canvas oder bei der Verwendung von Canvas in der Projektentwicklung auf ein solches Bedürfnis stoßen sollte: ein kleines Zeichenbrett zu implementieren, das geschrieben werden kann Werkzeug.
Nun, ich glaube, dass dies für Kinder, die mit Canvas vertraut sind, nur mit ein paar Dutzend Zeilen Code möglich ist. Die folgende Demo ist ein einfaches Beispiel:
nbsp;html>
<title>Sketchpad demo</title>
<style>
canvas {
border: 1px blue solid;
}
</style>
<canvas></canvas>
<script>
let isDown = false;
let beginPoint = null;
const canvas = document.querySelector('#canvas');
const ctx = canvas.getContext('2d');
// 设置线条颜色
ctx.strokeStyle = 'red';
ctx.lineWidth = 1;
ctx.lineJoin = 'round';
ctx.lineCap = 'round';
canvas.addEventListener('mousedown', down, false);
canvas.addEventListener('mousemove', move, false);
canvas.addEventListener('mouseup', up, false);
canvas.addEventListener('mouseout', up, false);
function down(evt) {
isDown = true;
beginPoint = getPos(evt);
}
function move(evt) {
if (!isDown) return;
const endPoint = getPos(evt);
drawLine(beginPoint, endPoint);
beginPoint = endPoint;
}
function up(evt) {
if (!isDown) return;
const endPoint = getPos(evt);
drawLine(beginPoint, endPoint);
beginPoint = null;
isDown = false;
}
function getPos(evt) {
return {
x: evt.clientX,
y: evt.clientY
}
}
function drawLine(beginPoint, endPoint) {
ctx.beginPath();
ctx.moveTo(beginPoint.x, beginPoint.y);
ctx.lineTo(endPoint.x, endPoint.y);
ctx.stroke();
ctx.closePath();
}
</script>
Nach dem Login kopieren
Seine Implementierungslogik ist auch sehr einfach:
Wir hören hauptsächlich drei Ereignisse auf der Leinwandleinwand: Mousedown, Mouseup und Mousemove, und wir erstellen auch eine isDown-Variable
Wenn der Benutzer die Maus drückt (Mousedown), setzen Sie isDown auf true, und wenn der Benutzer die Maus drückt (Mouseup), setzen Sie es auf false. Der Vorteil davon ist: Es kann beurteilt werden, ob Der Benutzer befindet sich derzeit im Zeichenstatus.
Erfassen Sie kontinuierlich die von der Maus über das Mousemove-Ereignis übergebenen Koordinatenpunkte, und zwar genau dann, wenn isDown wahr ist (d. h. im Schreibzustand) Der aktuelle Punkt wird über die lineTo-Methode von Canvas mit dem vorherigen Punkt verbunden und gezeichnet.
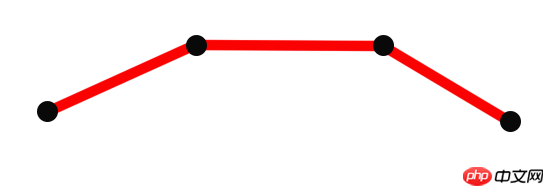
Durch die obigen Schritte können wir die grundlegende Zeichenbrettfunktion realisieren. Aber so einfach funktioniert das nicht. Bei vorsichtigen Kinderschuhen kann es zu einem sehr ernsten Problem kommen – die auf diese Weise gezeichneten Linien sind gezackt und nicht glatt genug, und je schneller Sie zeichnen, desto stärker wird das Faltgefühl. Die Leistung ist in der folgenden Abbildung dargestellt:
Warum ist das so?
Problemanalyse
Die Hauptgründe für dieses Phänomen sind:
-
Wir verbinden die Punkte mithilfe der lineTo-Methode von Canvas Die Verbindung zweier benachbarter Punkte ist eine gerade Linie und keine Kurve. Auf diese Weise wird also eine Polylinie gezeichnet 🎜>
Begrenzt durch die Erfassungshäufigkeit von Mausbewegungsereignissen durch den Browser, weiß jeder, dass der Browser während der Mausbewegung alle kurzen Zeiträume die Koordinaten der aktuellen Maus erfasst. Je schneller sich die Maus bewegt, desto größer ist also die Entfernung zwischen den beiden benachbarten Punkten, desto offensichtlicher ist das „Bruchkantengefühl“ 
Wie zeichnet man eine glatte Kurve? -
Tatsächlich gibt es Methoden zum Zeichnen glatter Kurven. Wenn lineTo unzuverlässig ist, können wir eine andere Zeichen-API von Canvas verwenden – quadraticCurveTo, die zum Zeichnen quadratischer Bezier-Kurven verwendet wird.
Quadratische Bezierkurve
quadraticCurveTo(cp1x, cp1y, x, y)
Für den Aufruf der quadraticCurveTo-Methode sind vier Parameter erforderlich: cp1x, cp1y beschreiben die Kontrollpunkte und x und y sind die Endpunkte der Kurve:
Detailliertere Informationen finden Sie auf MDN
Da Sie die Bezier-Kurve verwenden möchten , offensichtlich reichen unsere Daten nicht aus
Um eine quadratische Bezier-Kurve vollständig zu beschreiben, benötigen wir: Startpunkt, Kontrollpunkt und Endpunkt
Woher kommen diese Daten? 
Es gibt einen sehr cleveren Algorithmus, der uns helfen kann, diese Informationen zu erhalten
Algorithmus zum Erhalten quadratischer Bezier-Schlüsselpunkte
Dieser Algorithmus ist nicht schwer zu verstehen, hier werde ich direkt darauf eingehen Geben wir ein Beispiel:
Angenommen, wir sammeln insgesamt 6 Mauskoordinaten in einem Gemälde, nämlich A, B, C, D, E, F; 🎜>
Nehmen Sie die vorherigen drei Punkte A, B und C und berechnen Sie den Mittelpunkt B1 zwischen B und C. Mit A als Startpunkt, B als Kontrollpunkt und B1 als Endpunkt, Verwenden Sie quadraticCurveTo, um ein quadratisches Shell-Segment zu zeichnen Zeichnen Sie von den Punkten C und D aus Punkt C1 die Kurve weiter mit B1 als Startpunkt, C als Kontrollpunkt und C1 als Endpunkt >
Die Zeichnung wird analog fortgesetzt. Wenn sie den letzten Punkt F erreicht, endet die Bezier-Kurve mit D1, dem Mittelpunkt von D und E, als Ausgangspunkt, E als Kontrollpunkt und F als Endpunkt.
OK，算法就是这样，那我们基于该算法再对现有代码进行一次升级改造：
let isDown = false;
let points = [];
let beginPoint = null;
const canvas = document.querySelector('#canvas');
const ctx = canvas.getContext('2d');
// 设置线条颜色
ctx.strokeStyle = 'red';
ctx.lineWidth = 1;
ctx.lineJoin = 'round';
ctx.lineCap = 'round';
canvas.addEventListener('mousedown', down, false);
canvas.addEventListener('mousemove', move, false);
canvas.addEventListener('mouseup', up, false);
canvas.addEventListener('mouseout', up, false);
function down(evt) {
isDown = true;
const { x, y } = getPos(evt);
points.push({x, y});
beginPoint = {x, y};
}
function move(evt) {
if (!isDown) return;
const { x, y } = getPos(evt);
points.push({x, y});
if (points.length > 3) {
const lastTwoPoints = points.slice(-2);
const controlPoint = lastTwoPoints[0];
const endPoint = {
x: (lastTwoPoints[0].x + lastTwoPoints[1].x) / 2,
y: (lastTwoPoints[0].y + lastTwoPoints[1].y) / 2,
}
drawLine(beginPoint, controlPoint, endPoint);
beginPoint = endPoint;
}
}
function up(evt) {
if (!isDown) return;
const { x, y } = getPos(evt);
points.push({x, y});
if (points.length > 3) {
const lastTwoPoints = points.slice(-2);
const controlPoint = lastTwoPoints[0];
const endPoint = lastTwoPoints[1];
drawLine(beginPoint, controlPoint, endPoint);
}
beginPoint = null;
isDown = false;
points = [];
}
function getPos(evt) {
return {
x: evt.clientX,
y: evt.clientY
}
}
function drawLine(beginPoint, controlPoint, endPoint) {
ctx.beginPath();
ctx.moveTo(beginPoint.x, beginPoint.y);
ctx.quadraticCurveTo(controlPoint.x, controlPoint.y, endPoint.x, endPoint.y);
ctx.stroke();
ctx.closePath();
}Nach dem Login kopieren
在原有的基础上，我们创建了一个变量points用于保存之前mousemove事件中鼠标经过的点，根据该算法可知要绘制二次贝塞尔曲线起码需要3个点以上，因此我们只有在points中的点数大于3时才开始绘制。接下来的处理就跟该算法一毛一样了，这里不再赘述。
代码更新后我们的曲线也变得平滑了许多，如下图所示：
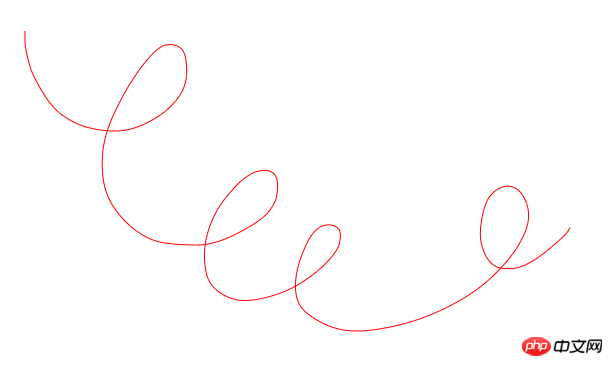
本文到这里就结束了，希望大家在canvas画板中“画”得愉快~我们下次再见：）
Das obige ist der detaillierte Inhalt vonWie zeichne ich glatte Kurven mit Canvas (Code). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
