Dieser Artikel bietet Ihnen eine detaillierte Einführung in JavaScript-Binärbäume (binäre Suchbäume). Ich hoffe, dass er für Freunde hilfreich ist.
Vielleicht gibt es einige Leute, die den Binärhaufen, den ich in meinem letzten Artikel geschrieben habe, nicht gelesen haben, daher habe ich das Grundkonzept des Binärbaums hier kopiert Sie können die vorherige Einführung in die Grundkonzepte von Binärbäumen ignorieren. Wenn Sie sich über die Datenstruktur der verknüpften Liste nicht im Klaren sind, werfen Sie außerdem einen Blick auf die zuvor geschriebene js-Datenstruktur Liste
Binärbaum (Binärbaum) ist eine Baumstruktur, die dadurch gekennzeichnet ist, dass jeder Knoten höchstens zwei Zweigknoten hat. Ein Binärbaum besteht normalerweise aus einem Wurzelknoten, Zweigknoten, und Blattknoten. Jeder Verzweigungsknoten wird oft als Unterbaum bezeichnet.
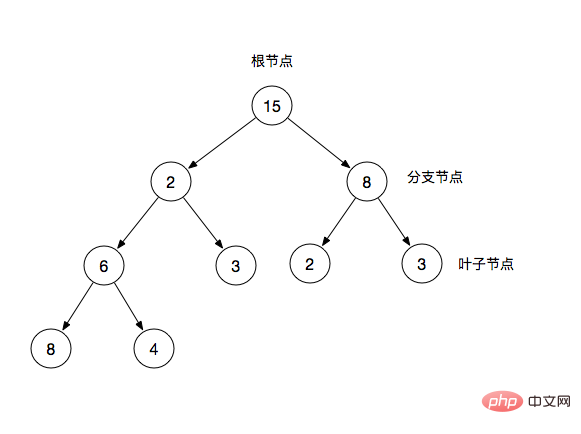
Wurzelknoten: der oberste Knoten des Binärbaums
Zweig Knoten: Zusätzlich zum Wurzelknoten und den Blattknoten
Blattknoten: Außer sich selbst gibt es keine anderen untergeordneten Knoten
Allgemeine Begriffe
In einem Binärbaum verwenden wir häufig übergeordnete Knoten und untergeordnete Knoten, um ihn zu beschreiben. Beispielsweise ist 2 im Bild der übergeordnete Knoten von 6 und 3, und umgekehrt sind 6 und 3 zwei untergeordnete Knoten Knoten.
Auf der i-ten Ebene des Binärbaums gibt es höchstens 2^i-1 Knoten
Wenn i=1, gibt es nur einen Wurzelknoten, 2^(i-1) = 2^0 = 1
Ein Binärbaum mit Tiefe k hat höchstens 2^k-1 Knoten
Wenn i=2, 2^k-1 = 2^2 - 1 = 3 Knoten
für jeden Baum Binärbaum T, wenn die Anzahl der Zusammenfassungspunkte n0 und die Anzahl der Knoten mit Grad 2 (die Anzahl der Teilbäume ist 2) n2 ist, dann n0=n2+1
Die Anzahl der Knoten in einem Baum beträgt mindestens 1, während die Anzahl der Knoten in einem Binärbaum 0 sein kann
Der maximale Grad der Knoten im Baum ( Es gibt keine Begrenzung für die Anzahl der Knoten), während der maximale Grad eines Knotens in einem Binärbaum ist 2 🎜>
BinärbaumklassifizierungBinärer Suchbaum erfüllt die folgenden Eigenschaften: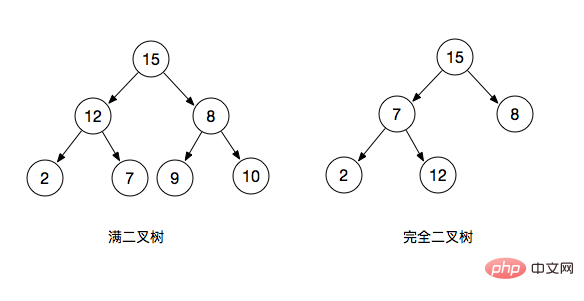 
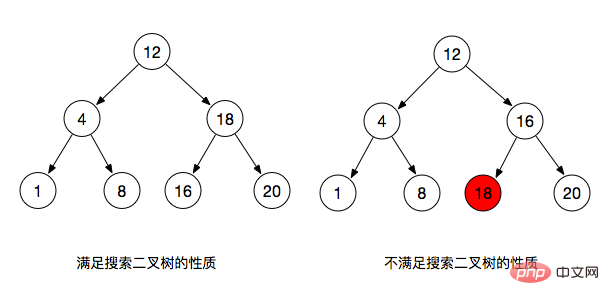
Wie aus der folgenden Abbildung ersichtlich ist, erfüllt die Abbildung links die Eigenschaften eines Binärbaums und jeder seiner linken untergeordneten Knoten ist kleiner als das übergeordnete Element Knoten, der rechte untergeordnete Knoten ist größer als sein übergeordneter Knoten, und die Knoten des linken Teilbaums sind kleiner als der Wurzelknoten, und die Knoten des rechten Teilbaums sind größer als der Wurzelknoten
Suchen
Einfügen
ein Zeiger auf den linken Knoten links
class BinaryTreeNode {
constructor(key, value){
this.parent = null;
this.left = null;
this.right = null;
this.key = key;
this.value = value;
}
}在二叉搜索树中我们会维护一个root指针，这个就相当于链表中的head指针，在没有任何节点插入的时候它指向空，在有节点插入以后它指向根节点。
class BinarySearchTree {
constructor() {
this.root = null;
}
} static createNode(key, value) {
return new BinarySearchTree(key, value);
}看下面这张图，13是我们要插入的节点，它插入的具体步骤：
跟根节点12做比较，比12大，所以我们确定了，这个节点是往右子树插入的
而根节点的右边已经有节点，那么跟这个节点18做比较，结果小于18所以往18的左节点找位置
而18的左节点也已经有节点了，所以继续跟这个节点做比较，结果小于16
刚好16的左节点是空的(left=null)，所以13这个节点就插入到了16的左节点
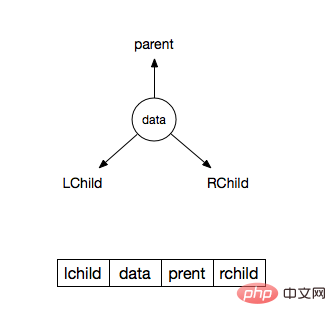
通过上面的描述，我们来看看代码是怎么写的
定义两个指针，分别是p和tail，最初都指向root，p是用来指向要插入的位置的父节点的指针，而tail是用来查找插入位置的，所以最后它会指向null，用上图举个例子，p最后指向了6这个节点，而tail最后指向了null（tail为null则说明已经找到了要插入的位置）
循环，tail根据我们上面分析的一步一步往下找位置插入，如果比当前节点小就往左找，大则往右找，一直到tail找到一个空位置也就是null
如果当前的root为null，则说明当前结构中并没有节点，所以插入的第一个节点直接为跟节点，即this.root = node
将插入后的节点的parent指针指向父节点
insert(node){
let p = this.root;
let tail = this.root;
// 循环遍历，去找到对应的位置
while(tail) {
p = tail;
// 要插入的节点key比当前节点小
if (node.key <h3>查找</h3><p>查找就很简单了，其实和插入差多，都是去别叫左右节点的大小，然后往下找</p>如果root = null, 则二叉树中没有任何节点，直接return，或者报个错什么的。
循环查找
search(key) {
let p = this.root;
if(!p) {
return;
}
while(p && p.key !== key){
if(p.key<key><h3>遍历</h3>
<ul class=" list-paddingleft-2">
<li><p>中序遍历(inorder)：先遍历左节点，再遍历自己，最后遍历右节点，输出的刚好是有序的列表</p></li>
<li><p>前序遍历(preorder)：先自己，再遍历左节点，最后遍历右节点</p></li>
<li><p>后序遍历(postorder)：先左节点，再右节点，最后自己</p></li>
</ul>
<p>最常用的一般是中序遍历，因为中序遍历可以得到一个已经排好序的列表，这也是为什么会用二叉搜索树排序的原因</p>
<p>根据上面对中序遍历的解释，那么代码就变的很简单，就是一个递归的过程，递归停止的条件就是节点为null</p>
<ul class=" list-paddingleft-2">
<li><p>先遍历左节点-->yield* this._transverse(node.left)</p></li>
<li><p>遍历自己 --> yield* node</p></li>
<li><p>遍历左节点 --> yield* this._transverse(node.right)</p></li>
</ul>
<pre class="brush:php;toolbar:false"> transverse() {
return this._transverse(this.root);
}
*_transverse(node){
if(!node){
return;
}
yield* this._transverse(node.left);
yield node;
yield* this._transverse(node.right)
}
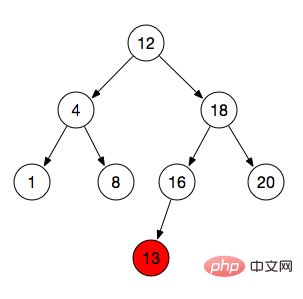
看上面这张图，我们简化的来看一下，先访问左节点4，再自己12，然后右节点18，这样输出的就刚好是一个12，4，8
补充：这个地方用了generater，所以返回的一个迭代器。可以通过下面这种方式得到一个有序的数组，这里的前提就当是已经有插入的节点了
const tree = new BinaryTree(); //...中间省略插入过程 // 这样就返回了一个有序的数组 var arr = [...tree.transverse()].map(item=>item.key);
class BinaryTreeNode {
constructor(key, value) {
// 指向父节点
this.p = null;
// 左节点
this.left = null;
// 右节点
this.right = null;
// 键
this.key = key;
// 值
this.value = value;
}
}
class BinaryTree {
constructor() {
this.root = null;
}
static createNode(key, value) {
return new BinaryTreeNode(key, value);
}
search(key) {
let p = this.root;
if (!p) {
return;
}
while (p && p.key !== key) {
if (p.key <h3>总结</h3><p>二叉查找树就讲完了哈，其实这个和链表很像的，还是操作那么几个指针，既然叫查找树了，它主要还是用来左一些搜索，还有就是排序了，另外补充一下，二叉查找树里找最大值和最小值也很方便是不是，如果你大致读懂了的话。</p><p class="comments-box-content"></p>Das obige ist der detaillierte Inhalt vonDetaillierte Einführung in JavaScript-Binärbäume (binäre Suchbäume). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
![[Web-Frontend] Node.js-Schnellstart](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
