Dieser Artikel bietet Ihnen eine Einführung in die Methode zur Implementierung rekursiver Algorithmen. Ich hoffe, dass er für Freunde hilfreich ist.
Schauen wir uns zunächst die Definition an. Ein rekursiver Algorithmus wandelt ein Problem in verkleinerte Unterprobleme desselben Typs um, und jedes Unterproblem wird mit demselben Algorithmus gelöst. Im Allgemeinen ist ein rekursiver Algorithmus eine Funktion, die sich selbst aufruft, um ihre Teilprobleme zu lösen.
Eigenschaften des rekursiven Algorithmus:
- ruft sich während des Funktionsablaufs selbst auf.
- Während des rekursiven Prozesses muss eine klare Bedingung vorliegen, um das Ende der Rekursion, also den rekursiven Ausgang, zu bestimmen.
- Der rekursive Algorithmus ist einfach, aber ineffizient und wird normalerweise nicht als empfohlener Algorithmus empfohlen.
Die oben genannten Erklärungen stammen aus der Baidu-Enzyklopädie und sind sehr klar. Bitte betrachten Sie sie sorgfältig anhand von Beispielen.
Fakultät
Problembeschreibung: n! = n*(n-1)*...2*1
Code-Implementierung:
Wenn wir das Problem bekommen, können wir zunächst die Größe auf ähnliche Unterprobleme gemäß der Definition reduzieren. Zum Beispiel ist n! gleich n* (n-1)!, dann ist (n-1)! = (n-1)*(n-2)!. Drücken Sie in dieser Reihenfolge bis zum Ausgang von if nach unten. arguments.callee wird hier verwendet, um eine enge Kopplung von Funktionsnamen zu verhindern. Hier ist es äquivalent zu factial(n-1). Ist die Funktionsimplementierung einfach und klar? Da das Ausmaß des Problems einfach ist, kann es natürlich mithilfe von Schleifen implementiert werden. Sie können es versuchen.
Fibonacci-Folge
Problembeschreibung: 1, 1, 2, 3, 5, 8, 13, 21, 34, ... .... Finden Sie die n-te Zahl.
Code-Implementierung:
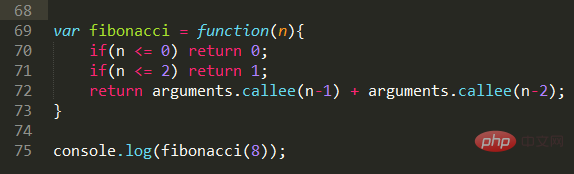
Tatsächlich ist es gerade jetzt sehr einfach, die Idee umzusetzen. Durch Analyse können wir die n-te Zahl erhalten, die die Summe der ersten beiden Zahlen ist. Dadurch können wir durch Rekursion weiterhin die ersten beiden Zahlen erhalten, die wir benötigen, bis die Bedingung n
Das Problem beim Treppensteigen
Problembeschreibung: Es gibt n Stufen in der Treppe. Man kann eine Stufe in einer Stufe hinaufgehen oder 2 Schritte in einem Schritt. Oder Level 3, zählen Sie, wie viele verschiedene Züge es gibt.
Code-Implementierung:
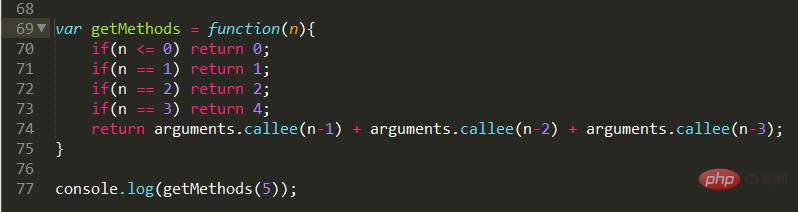
Dies ist eigentlich eine Implementierung der Fibonacci-Folge. Wenn wir es analysieren, können wir es in kleine Unterklassenprobleme umwandeln. Beim Erreichen der letzten Stufe der vorgesehenen Leiter kann es drei Situationen geben: Eine ist eine Stufe höher, zwei bedeutet zwei Stufen höher und drei sind drei Stufen höher. Die Gesamtmethode lautet also F(n) = F(n-1) + F(n-2) + F(n-3). Dann wird es natürlich zu ihrer eigenen kleinen Berechnung, und der Zyklus geht weiter, bis die Beurteilungsbedingung eintritt.
Größter gemeinsamer Teiler
Problembeschreibung: Wenn zwei Zahlen gegeben sind und die beiden Zahlen gleich sind, ist der größte gemeinsame Teiler er selbst. Wenn sie nicht gleich sind, nehmen Sie den Absolutwert der Subtraktion der beiden Zahlen und vergleichen Sie ihn mit der kleinsten der beiden Zahlen. Wenn sie gleich sind, ist es der größte gemeinsame Nenner. Wenn sie nicht gleich sind, fahren Sie mit dem obigen Algorithmus fort bis sie gleich sind.
Code-Implementierung:
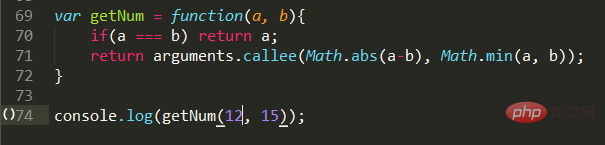
Es gibt nichts zu sagen, implementieren Sie es einfach wie in der Problembeschreibung gefordert. Das Ergebnis der Rekursion ist, dass a gleich b ist.
Turm von Hanoi
Problembeschreibung: Jeder hat es mehr oder weniger gespielt, daher werde ich hier nicht auf Details eingehen.
Code-Implementierung:
Bevor ich das Wesen der Rekursion erkannte, war ich einfach verwirrt über dieses Problem. Ich frage mich immer wieder: Woher weiß ich, wohin ich als nächstes gehen soll? Später wurde mir klar, dass ich mir beim letzten Mal eigentlich mehr Gedanken darüber machte, wie ich vorgehen sollte. Wie sagt man das? Wir können von Anfang an denken: Wenn wir nur eine Festplatte haben, können wir sie in Spalte C oder Spalte B verschieben. Selbstverständlich ist dies auch mit zwei Scheiben möglich. 3 Festplatten sind in Ordnung. Dann lassen Sie uns über die Situation von 4 Festplatten sprechen. Um die vier Festplatten fertigzustellen, muss die Festplatte von A vollständig nach C übertragen werden. Wir haben die ersten drei Festplatten als Ganzes auf B gelegt, und dann kann die vierte Festplatte nach C verschoben werden. Dann haben wir die ersten drei Festplatten auf C gelegt und es war erfolgreich. Die ersten drei Spiele können als neues Spiel behandelt werden, die ersten beiden Spiele können als Ganzes behandelt werden und so weiter. Auf diese Weise müssen wir uns nur um die großen Gesamtthemen kümmern, und der Rest kann auf kleine, zu lösende Probleme reduziert werden.
DichotomieSchnellsortierung
Problembeschreibung: Verwenden Sie die Dichotomiemethode, um ein Array von klein nach groß zu sortieren.
Code-Implementierung:
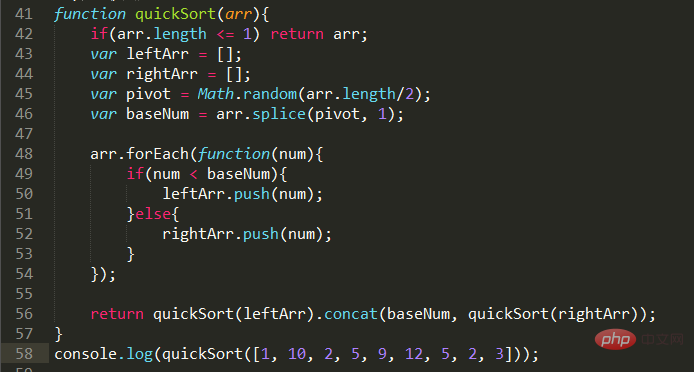
Hmm...das ist das zweite Mal, dass ich das schreibe. Diesmal ist die Implementierung der Rekursion viel klarer als beim letzten Mal. Tatsächlich geht es auch darum, den großen Maßstab auf den kleinen Maßstab zu reduzieren, sich um ein großes Ganzes zu kümmern und es für die Berechnung weiterhin auf den kleinen Maßstab reduzieren zu lassen. Einzelheiten finden Sie im Originalaufsatz.
Rekursion des DOM-Baums
Problembeschreibung: Den tagName aller übergeordneten Knoten eines Knotens abrufen
Code-Implementierung:
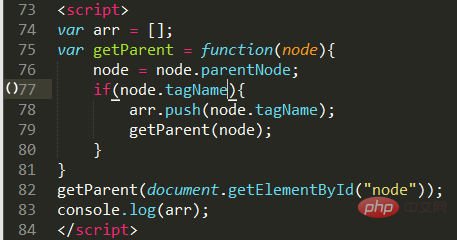
Du kannst es wahrscheinlich verstehen und wirst nichts sagen. Im Vergleich zum vorherigen Tower of Hanoi und Quick Sort ist dieser recht einfach, kommt aber der praktischen Anwendung unseres JavaScripts am nächsten.
Dieser Artikel ist hier zu Ende. Weitere spannende Inhalte finden Sie in der Spalte JavaScript-Video-Tutorial auf der chinesischen PHP-Website!
Das obige ist der detaillierte Inhalt vonEinführung in Methoden zur Implementierung rekursiver Algorithmen in JavaScript. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
