Wie man Datenstrukturen und Algorithmen versteht (Python)

Verständnis von Datenstrukturen und Algorithmen in Python: Datenstrukturen in Python beziehen sich auf die statische Beschreibung der Beziehung zwischen Datenelementen, und Algorithmen beziehen sich auf Methoden oder Schritte zur Lösung von Problemen. Mit anderen Worten: Algorithmen sind darauf ausgelegt, praktische Probleme zu lösen Die Datenstruktur ist der Träger des Problems, mit dem sich der Algorithmus befassen muss.

Datenstruktur und Algorithmus sind wesentliche Grundkenntnisse für einen Programmentwickler, daher müssen wir die Initiative ergreifen, sie zu erlernen und zu akkumulieren. Als nächstes werde ich Ihnen diese beiden Wissenspunkte im Detail vorstellen Ich hoffe, es wird Ihnen helfen.

[Empfohlene Kurse: Python-Tutorial]

Einführung in das Konzept

Schauen wir uns zunächst eine Frage an:

Wenn a+b+c=1000 und a2+b2=c^2 (a, b, c sind natürliche Zahlen), wie finde ich alle möglichen Kombinationen von a, b, c?

Erster Versuch

import time
start_time = time.time()
# 注意是三重循环
for a in range(0, 1001):    
for b in range(0, 1001):        
for c in range(0, 1001):            
if a**2 + b**2 == c**2 and a+b+c == 1000:
print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()
print("elapsed: %f" % (end_time - start_time))
print("complete!")

Laufendes Ergebnis:

a, b, c: 0, 500, 500
a, b, c: 200, 375, 425
a, b, c: 375, 200, 425
a, b, c: 500, 0, 500
elapsed: 1066.117884
complete!

Die Laufzeit beträgt bis zu 17,8 Minuten

Vorschlag des Algorithmus

Konzept des Algorithmus

Algorithmen sind die Essenz der Art und Weise, wie Computer Informationen verarbeiten, denn ein Computerprogramm ist im Wesentlichen ein Algorithmus, der dem Computer die genauen Schritte zur Ausführung einer bestimmten Aufgabe mitteilt. Wenn ein Algorithmus Informationen verarbeitet, liest er im Allgemeinen Daten von einem Eingabegerät oder einer Speicheradresse der Daten und schreibt die Ergebnisse zum späteren Abruf auf ein Ausgabegerät oder eine Speicheradresse.
Algorithmen sind eigenständige Methoden und Ideen zur Lösung von Problemen.
Für Algorithmen ist die Sprache der Implementierung nicht wichtig, wichtig ist die Idee.
Der Algorithmus kann verschiedene Sprachbeschreibungen und Implementierungsversionen haben (z. B. C-Beschreibung, C++-Beschreibung, Python-Beschreibung usw.), um ihn zu beschreiben und zu implementieren.

Fünf Merkmale von Algorithmen

Eingabe: Der Algorithmus hat 0 oder mehr Eingaben

Ausgabe: Der Algorithmus hat mindestens 1 oder mehr Ausgaben

Endlichkeit: Der Algorithmus endet automatisch nach einer begrenzten Anzahl von Schritten ohne Endlosschleife, und jeder Schritt kann innerhalb einer akzeptablen Zeit abgeschlossen werden

Deterministisch: Jeder Schritt im Algorithmus hat alle eine bestimmte Bedeutung und ist vorhanden wird keine Mehrdeutigkeit geben

Machbarkeit: Jeder Schritt des Algorithmus ist machbar, was bedeutet, dass jeder Schritt eine begrenzte Anzahl von Malen ausgeführt werden kann

Zweiter Versuch

import time
start_time = time.time()
# 注意是两重循环
for a in range(0, 1001):    
for b in range(0, 1001-a):
c = 1000 - a - b        
if a**2 + b**2 == c**2:            
print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()print("elapsed: %f" % (end_time - start_time))print("complete!")

Laufergebnisse:

a, b, c: 0, 500, 500
a, b, c: 200, 375, 425
a, b, c: 375, 200, 425
a, b, c: 500, 0, 500
elapsed: 0.632128

Beachten Sie, dass die Laufzeit 0,632128 Sekunden beträgt

Algorithmuseffizienzmessung

Ausführungszeit-Reaktionsalgorithmus Effizienz

Für das gleiche Problem haben wir zwei Lösungsalgorithmen angegeben. Bei der Implementierung der beiden Algorithmen haben wir festgestellt, dass die Ausführungszeit der beiden Programme sehr unterschiedlich ist Daraus können wir eine Schlussfolgerung ziehen: Die Ausführungszeit des Algorithmusprogramms kann die Effizienz des Algorithmus widerspiegeln, dh die Qualität des Algorithmus.

Ist der Zeitwert allein absolut zuverlässig?

Was wäre, wenn wir unseren zweiten Versuch des Algorithmus auf einem Computer mit einer alten, leistungsschwachen Konfiguration ausführen würden? Höchstwahrscheinlich wird die Laufzeit nicht viel schneller sein als die Ausführung von Algorithmus 1 auf unserem Computer.

Es ist nicht unbedingt objektiv und genau, die Vor- und Nachteile von Algorithmen ausschließlich auf der Grundlage der Laufzeit zu vergleichen!

Die Ausführung eines Programms kann nicht von der Computerumgebung (einschließlich Hardware und Betriebssystem) getrennt werden. Diese objektiven Gründe wirken sich auf die Geschwindigkeit des Programms aus und spiegeln sich in der Ausführungszeit des Programms wider. Wie können wir also die Qualität eines Algorithmus objektiv beurteilen?

Zeitkomplexität und „Big-O-Notation“

Wir gehen davon aus, dass die Zeit, die der Computer benötigt, um jede Grundoperation des Algorithmus auszuführen, eine feste Zeiteinheit ist. Wie viele Grundoperationen stellen also dar, wie viele Zeiteinheiten dafür benötigt werden? Da die genaue Zeiteinheit für verschiedene Maschinenumgebungen unterschiedlich ist, die Anzahl der vom Algorithmus ausgeführten Grundoperationen (dh wie viele Zeiteinheiten er benötigt) jedoch in der Größenordnung gleich ist, kann der Einfluss der Maschinenumgebung variieren ignoriert werden und objektiv Die Zeiteffizienz des Reaktionsalgorithmus.

Für die Zeiteffizienz des Algorithmus können wir die „Big O-Notation“ verwenden, um ihn auszudrücken.

„Große O-Notation“: Für eine monotone Ganzzahlfunktion f, wenn es eine Ganzzahlfunktion g und eine reelle Konstante c>0 gibt, so dass für ein ausreichend großes n immer f(n)< =c* g(n), man sagt, dass die Funktion g eine asymptotische Funktion von f ist (ohne Berücksichtigung der Konstanten), aufgezeichnet als f(n)=O(g(n)). Das heißt, im Grenzsinne der Tendenz zur Unendlichkeit wird die Wachstumsrate der Funktion f durch die Funktion g eingeschränkt, das heißt, die Eigenschaften von Funktion f und Funktion g sind ähnlich.

Zeitkomplexität: Angenommen, es gibt eine Funktion g, so dass die Zeit, die Algorithmus A benötigt, um ein Problembeispiel der Größe n zu verarbeiten, T(n)=O(g(n)) ist, dann wird sie aufgerufen O(g(n)) ist die asymptotische Zeitkomplexität des Algorithmus A, die als Zeitkomplexität bezeichnet wird und als T(n) bezeichnet wird

Wie man die „Big O-Notation“ versteht

对于算法进行特别具体的细致分析虽然很好，但在实践中的实际价值有限。对于算法的时间性质和空间性质，最重要的是其数量级和趋势，这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。例如，可以认为3n2和100n2属于同一个量级，如果两个算法处理同样规模实例的代价分别为这两个函数，就认为它们的效率“差不多”，都为n2级。

最坏时间复杂度

分析算法时，存在几种可能的考虑：

算法完成工作最少需要多少基本操作，即最优时间复杂度

算法完成工作最多需要多少基本操作，即最坏时间复杂度

算法完成工作平均需要多少基本操作，即平均时间复杂度
对于最优时间复杂度，其价值不大，因为它没有提供什么有用信息，其反映的只是最乐观最理想的情况，没有参考价值。

对于最坏时间复杂度，提供了一种保证，表明算法在此种程度的基本操作中一定能完成工作。

对于平均时间复杂度，是对算法的一个全面评价，因此它完整全面的反映了这个算法的性质。但另一方面，这种衡量并没有保证，不是每个计算都能在这个基本操作内完成。而且，对于平均情况的计算，也会因为应用算法的实例分布可能并不均匀而难以计算。

因此，我们主要关注算法的最坏情况，亦即最坏时间复杂度。

时间复杂度的几条基本计算规则

基本操作，即只有常数项，认为其时间复杂度为O(1)

顺序结构，时间复杂度按加法进行计算

循环结构，时间复杂度按乘法进行计算

分支结构，时间复杂度取最大值

判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略

在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度

算法分析

第一次尝试的算法核心部分

or a in range(0, 1001):    
for b in range(0, 1001):        
for c in range(0, 1001):            
if a**2 + b**2 == c**2 and a+b+c == 1000:
print("a, b, c: %d, %d, %d" % (a, b, c))

时间复杂度：

T(n) = O(n * n * n) = O(n³)

第二次尝试的算法核心部分

for a in range(0, 1001):    
for b in range(0, 1001-a):
c = 1000 - a - b        
if a**2 + b**2 == c**2:            
print("a, b, c: %d, %d, %d" % (a, b, c))

时间复杂度：

T(n) = O(n * n * (1+1)) = O(n * n) = O(n²)

由此可见，我们尝试的第二种算法要比第一种算法的时间复杂度好多的。

常见时间复杂度

执行次数函数举例	阶	非正式术语
12	O(1)	常数阶
2n + 3	O(n)	线性阶
3n² +2n + 1	O(n²)	平方阶
5log2n+20	O(logn)	对数阶
2n+3nlog2n+19	O(nlogn)	nlogn阶
6n³ +2n² +3n + 1	O(n³)	立方阶
2n	O(2n)	指数阶

注意，经常将log2n（以2为底的对数）简写成logn

常见时间复杂度之间的关系

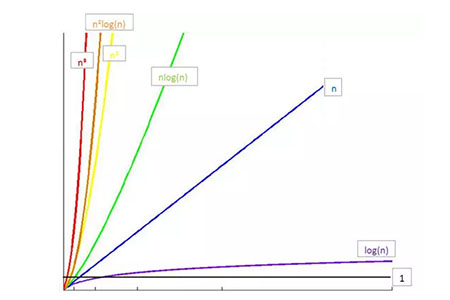
所消耗的时间从小到大

O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)

Python内置类型性能分析

timeit模块

timeit模块可以用来测试一小段Python代码的执行速度。

class timeit.Timer(stmt=&#39;pass&#39;, setup=&#39;pass&#39;, timer=<timer function>)

Timer是测量小段代码执行速度的类。

stmt参数是要测试的代码语句（statment）

setup参数是运行代码时需要的设置

timer参数是一个定时器函数，与平台有关。

timeit.Timer.timeit(number=1000000)

Timer类中测试语句执行速度的对象方法。number参数是测试代码时的测试次数，默认为1000000次。方法返回执行代码的平均耗时，一个float类型的秒数。

list的操作测试

def test1():
   l = []   for i in range(1000):
      l = l + [i]def test2():
   l = []   for i in range(1000):
      l.append(i)def test3():
   l = [i for i in range(1000)]def test4():
   l = list(range(1000))from timeit import Timer
t1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "seconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "seconds")
t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "seconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "seconds")
# ('concat ', 1.7890608310699463, 'seconds')
# ('append ', 0.13796091079711914, 'seconds')
# ('comprehension ', 0.05671119689941406, 'seconds')
# ('list range ', 0.014147043228149414, 'seconds')

pop操作测试

x = range(2000000)
pop_zero = Timer("x.pop(0)","from __main__ import x")
print("pop_zero ",pop_zero.timeit(number=1000), "seconds")
x = range(2000000)
pop_end = Timer("x.pop()","from __main__ import x")
print("pop_end ",pop_end.timeit(number=1000), "seconds")
# ('pop_zero ', 1.9101738929748535, 'seconds')
# ('pop_end ', 0.00023603439331054688, 'seconds')

测试pop操作：从结果可以看出，pop最后一个元素的效率远远高于pop第一个元素

可以自行尝试下list的append(value)和insert(0,value),即一个后面插入和一个前面插入？？？

list内置操作的时间复杂度

dict内置操作的时间复杂度

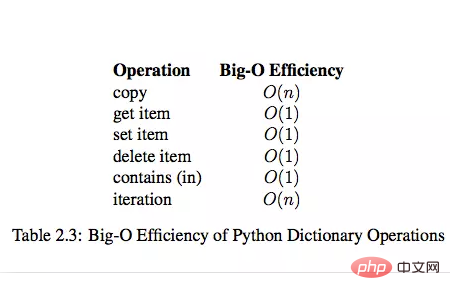
数据结构

概念

数据是一个抽象的概念，将其进行分类后得到程序设计语言中的基本类型。如：int，float，char等。数据元素之间不是独立的，存在特定的关系，这些关系便是结构。数据结构指数据对象中数据元素之间的关系。

Python给我们提供了很多现成的数据结构类型，这些系统自己定义好的，不需要我们自己去定义的数据结构叫做Python的内置数据结构，比如列表、元组、字典。而有些数据组织方式，Python系统里面没有直接定义，需要我们自己去定义实现这些数据的组织方式，这些数据组织方式称之为Python的扩展数据结构，比如栈，队列等。

算法与数据结构的区别

数据结构只是静态的描述了数据元素之间的关系。

高效的程序需要在数据结构的基础上设计和选择算法。

程序 = 数据结构 + 算法

总结：算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题载体

抽象数据类型(Abstract Data Type)

抽象数据类型(ADT)的含义是指一个数学模型以及定义在此数学模型上的一组操作。即把数据类型和数据类型上的运算捆在一起，进行封装。引入抽象数据类型的目的是把数据类型的表示和数据类型上运算的实现与这些数据类型和运算在程序中的引用隔开，使它们相互独立。

最常用的数据运算有五种

插入

删除

修改

查找

排序

Das obige ist der detaillierte Inhalt vonWie man Datenstrukturen und Algorithmen versteht (Python). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!