Grafisches Durchlaufen der Ebenenreihenfolge in C++ und schichtweises Drucken von Binärbäumen, die durch intelligente Zeiger erstellt wurden

Binärbäume sind eine äußerst verbreitete Datenstruktur und es gibt unzählige Artikel darüber, wie man ihre Elemente durchquert. In den meisten Artikeln wird jedoch das Durchqueren von Vorbestellungen, Zwischenbestellungen und Nachbestellungen erläutert. Es gibt nicht viele Artikel zum schichtweisen Drucken von Elementen. Die Erklärungen in vorhandenen Artikeln sind ebenfalls relativ unklar und schwer zu lesen. In diesem Artikel werden anschauliche Bilder und klarer Code verwendet, um Ihnen das Verständnis der Implementierung des Level-Order-Traversals zu erleichtern. Gleichzeitig verwenden wir intelligente Zeiger, die von modernem C++ bereitgestellt werden, um die Ressourcenverwaltung von Baumdatenstrukturen zu vereinfachen.

Verwandte Tutorials: Tutorial zum Datenstrukturbaum

Kommen wir nun zum Punkt.

Konstruieren Sie einen Binärbaum mit intelligenten Zeigern

Was wir hier implementieren möchten, ist ein Binärbaum, der einfach einen binären Suchbaum simuliert und eine Einfügefunktion bereitstellt, die die Anforderungen eines binären Suchbaums erfüllt , einschließlich In-Order-Traversal. Gleichzeitig verwenden wir shared_ptr, um Ressourcen zu verwalten.

Jetzt implementieren wir nur zwei Methoden: insert und ldr Die Implementierung der anderen Methoden ist nicht das, worum es in diesem Artikel geht, aber wir werden sie in den folgenden Artikeln einzeln vorstellen:

struct BinaryTreeNode: public std::enable_shared_from_this<BinaryTreeNode> {
    explicit BinaryTreeNode(const int value = 0)
    : value_{value}, left{std::shared_ptr<BinaryTreeNode>{}}, right{std::shared_ptr<BinaryTreeNode>{}}
    {}

    void insert(const int value)
    {
        if (value < value_) {
            if (left) {
                left->insert(value);
            } else {
                left = std::make_shared<BinaryTreeNode>(value);
            }
        }

        if (value > value_) {
            if (right) {
                right->insert(value);
            } else {
                right = std::make_shared<BinaryTreeNode>(value);
            }
        }
    }

    // 中序遍历
    void ldr()
    {
        if (left) {
            left->ldr();
        }

        std::cout << value_ << "\n";

        if (right) {
            right->ldr();
        }
    }

    // 分层打印
    void layer_print();

    int value_;
    // 左右子节点
    std::shared_ptr<BinaryTreeNode> left;
    std::shared_ptr<BinaryTreeNode> right;

private:
    // 层序遍历
    std::vector<std::shared_ptr<BinaryTreeNode>> layer_contents();
};

Unser Knotenobjekt erbt von enable_shared_from_this, normalerweise ist dies nicht notwendig, aber um den Betrieb während der Durchquerung der Ebenenreihenfolge zu erleichtern, müssen wir einen intelligenten Zeiger von this erstellen, daher ist dieser Schritt notwendig. insert fügt Elemente, die kleiner als die Wurzel sind, in den linken Teilbaum ein, und Elemente, die größer als die Wurzel sind, werden in den rechten Teilbaum eingefügt. ldr ist die konventionellste Durchquerung in der Reihenfolge. Sie wird hier implementiert, um alle Elemente im Baum anzuzeigen auf herkömmliche Weise.

Es ist zu beachten, dass es am besten ist, make_shared zu verwenden, um sie zu erstellen, anstatt sie als globale/lokale Objekte zu initialisieren. Andernfalls wird es beim Durchlaufen der Ebenenreihenfolge zerstört Die Zerstörung von shared_ptr führt zur Zerstörung des Objekts, was zu undefiniertem Verhalten führt.

Angenommen, wir haben einen Datensatz: [3, 1, 0, 2, 5, 4, 6, 7], nehmen das erste Element als Wurzel und fügen alle Daten in unseren Baum ein Das Ergebnis ist der folgende Binärbaum:

auto root = std::make_shared<BinaryTreeNode>(3);
root->insert(1);
root->insert(0);
root->insert(2);
root->insert(5);
root->insert(4);
root->insert(6);
root->insert(7);

Sie können sehen, dass die Knoten in vier Schichten unterteilt sind. Jetzt müssen wir Schicht für Schicht drucken.

Durchquerung der Ebenenreihenfolge

Tatsächlich ist die Idee sehr einfach. Wir übernehmen die Breite-zuerst-Idee: Drucken Sie zuerst alle Kinder des Knotens und dann die Kinder des Kindes Knoten.

Nehmen Sie das obige Bild als Beispiel. Wir drucken zuerst den Wert des Wurzelknotens 3 und dann die Werte aller seiner untergeordneten Knoten, nämlich 1 und 5 und dann die untergeordneten Knoten des linken und rechten untergeordneten Knotens und so weiter. . . . . .

Es ist leicht zu sagen, aber es wird mühsam sein, den Code zu schreiben. Wir können das Problem nicht einfach mit der Rekursion lösen, wie beim Durchlaufen in der Reihenfolge (tatsächlich können wir einen verbesserten rekursiven Algorithmus verwenden), da diese direkt zu den Blattknoten führt, was nicht das gewünschte Ergebnis ist. Aber es spielt keine Rolle, wir können die Warteschlange verwenden, um die untergeordnete Knotenwarteschlange am Ende der Warteschlange hinzuzufügen, dann vom Anfang der Warteschlange, dem Wurzelknoten, durchlaufen, ihre untergeordneten Knoten zur Warteschlange hinzufügen und dann Führen Sie den gleichen Vorgang am zweiten Knoten aus. Wenn Sie auf das Ende einer Zeile stoßen, markieren wir es mit nullptr.

Schauen Sie sich zuerst den spezifischen Code an:

std::vector<std::shared_ptr<BinaryTreeNode>>
BinaryTreeNode::layer_contents()
{
    std::vector<std::shared_ptr<BinaryTreeNode>> nodes;
    // 先添加根节点，根节点自己就会占用一行输出，所以添加了作为行分隔符的nullptr
    // 因为需要保存this，所以这是我们需要继承enable_shared_from_this是理由
    // 同样是因为这里，当返回的结果容器析构时this的智能指针也会析构
    // 如果我们使用了局部变量则this的引用计数从1减至0，导致对象被销毁，而使用了make_shared创建的对象引用计数是从2到1，没有问题
    nodes.push_back(shared_from_this());
    nodes.push_back(nullptr);
    // 我们使用index而不是迭代器，是因为添加元素时很可能发生迭代器失效，处理这一问题将会耗费大量精力，而index则无此烦恼
    for (int index = 0; index < nodes.size(); ++index) {
        if (!nodes[index]) {
            // 子节点打印完成或已经遍历到队列末尾
            if (index == nodes.size()-1) {
                break;
            }

            nodes.push_back(nullptr); // 添加分隔符
            continue;
        }

        if (nodes[index]->left) { // 将当前节点的子节点都添加进队列
            nodes.push_back(nodes[index]->left);
        }
        if (nodes[index]->right) {
            nodes.push_back(nodes[index]->right);
        }
    }

    return nodes;
}

Der Code selbst ist nicht kompliziert, wichtig ist die Idee dahinter.

Illustration des Algorithmus

Es spielt keine Rolle, ob Sie diesen Code beim ersten Mal nicht verstehen. Wir stellen Ihnen unten ein Diagramm zur Verfügung:

Das erste ist das Zustand am Anfang der Schleife wurde bestimmt (^ stellt einen Nullzeiger dar):

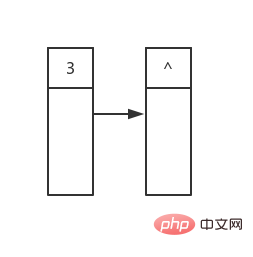
Dann beginnen wir mit dem Durchlauf vom ersten Element Das erste, das durchquert wird, ist root, das zwei untergeordnete Elemente hat. Die Werte sind 1 bzw. 5:

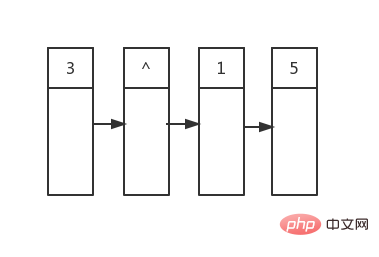
Dann ist der Indexwert +1, dieses Mal geht es nach nullptr, Da es sich nicht am Ende der Warteschlange befindet, fügen wir einfach einen nullptr am Ende der Warteschlange hinzu, sodass sich die Knoten in der zweiten Reihe alle in der Warteschlange befinden:

Dann beginnen wir mit dem Durchlaufen der Knoten in der zweiten Zeile und verwenden deren untergeordnete Knoten als Der Inhalt der drei Zeilen wird in die Warteschlange gestellt, am Ende wird ein Zeilentrenner hinzugefügt und so weiter:

Um es einfach auszudrücken: Alle Knoten der vorherigen Zeile werden über die Warteschlange zwischengespeichert. Anschließend werden alle Knoten der nächsten Zeile basierend auf dem Cache der vorherigen Zeile abgerufen Der Zyklus wird bis zur letzten Ebene des Binärbaums fortgesetzt. Natürlich können mit ähnlichen Ideen nicht nur Binärbäume, sondern auch das Durchlaufen anderer Multibäume in Ebenenordnung implementiert werden.

Okay, da wir nun wissen, wie wir den Inhalt jeder Zeile erhalten, können wir die Knoten Zeile für Zeile verarbeiten:

void BinaryTreeNode::layer_print()
{
    auto nodes = layer_contents();
    for (auto iter = nodes.begin(); iter != nodes.end(); ++iter) {
        // 空指针代表一行结束，这里我们遇到空指针就输出换行符
        if (*iter) {
            std::cout << (*iter)->value_ << " ";
        } else {
            std::cout << "\n";
        }
    }
}

如你所见，这个方法足够简单，我们把节点信息保存在额外的容器中是为了方便做进一步的处理，如果只是打印的话大可不必这么麻烦，不过简单通常是有代价的。对于我们的实现来说，分隔符的存在简化了我们对层级之间的区分，然而这样会导致浪费至少log2(n)+1个vector的存储空间，某些情况下可能引起性能问题，而且通过合理得使用计数变量可以避免这些额外的空间浪费。当然具体的实现读者可以自己挑战一下，原理和我们上面介绍的是类似的因此就不在赘述了，也可以参考园内其他的博客文章。

测试

最后让我们看看完整的测试程序，记住要用make_shared创建root实例：

int main()
{
    auto root = std::make_shared<BinaryTreeNode>(3);
    root->insert(1);
    root->insert(0);
    root->insert(2);
    root->insert(5);
    root->insert(4);
    root->insert(6);
    root->insert(7);
    root->ldr();
    std::cout << "\n";
    root->layer_print();
}

输出：

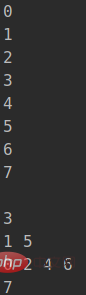
可以看到上半部分是中序遍历的结果，下半部分是层序遍历的输出，而且是逐行打印的，不过我们没有做缩进。所以不太美观。

另外你可能已经发现了，我们没有写任何有关资源释放的代码，没错，这就是智能指针的威力，只要注意资源的创建，剩下的事都可以放心得交给智能指针处理，我们可以把更多的精力集中在算法和功能的实现上。

如有错误和疑问欢迎指出！

Das obige ist der detaillierte Inhalt vonGrafisches Durchlaufen der Ebenenreihenfolge in C++ und schichtweises Drucken von Binärbäumen, die durch intelligente Zeiger erstellt wurden. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!