Grundlegende Eigenschaften von Binärbäumen

In der Informatik ist ein Binärbaum eine Baumstruktur mit höchstens zwei Teilbäumen pro Knoten. Normalerweise werden Teilbäume als „linker Teilbaum“ und „rechter Teilbaum“ bezeichnet. Binärbäume werden häufig zur Implementierung binärer Suchbäume und binärer Heaps verwendet.

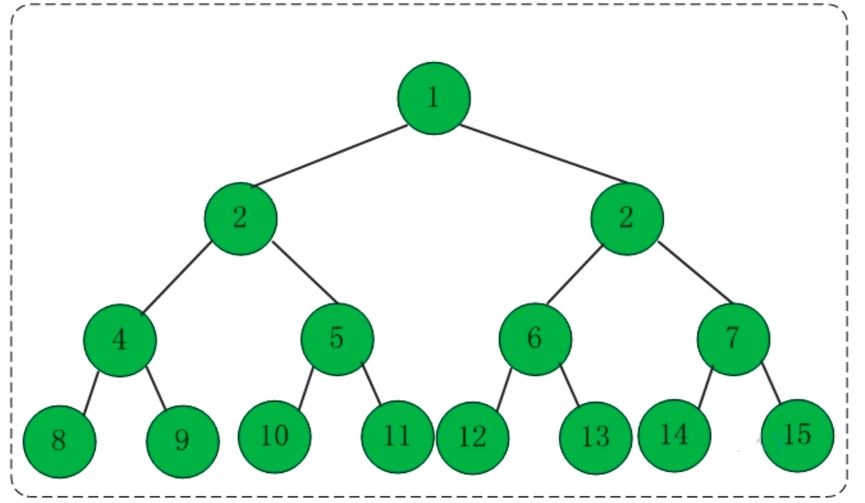
Ein Binärbaum mit der Tiefe k und 2^k-1 Knoten wird als vollständiger Binärbaum bezeichnet. Das Merkmal dieser Art von Baum ist, dass die Anzahl der Knoten auf jeder Ebene der maximalen Anzahl von Knoten entspricht. Wenn in einem Binärbaum alle Ebenen außer der letzten Ebene voll sind und die letzte Ebene entweder voll ist oder rechts mehrere aufeinanderfolgende Knoten fehlen, dann ist der Binärbaum ein vollständiger Binärbaum. Die Tiefe eines vollständigen Binärbaums mit n Knoten beträgt floor(log2n)+1. Ein vollständiger Binärbaum mit Tiefe k hat mindestens 2k-1 Blattknoten und höchstens 2k-1 Knoten.

Binärbaumeigenschaften

(1) In einem nicht leeren Binärbaum überschreitet die Gesamtzahl der Knoten auf der i-ten Ebene nicht 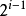, i>=1;

(2) Ein Binärbaum mit der Tiefe h hat höchstens 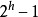Knoten (h>=1) und mindestens h Knoten; Binärbaum, wenn die Anzahl der Blattknoten N0 ist und die Gesamtzahl der Knoten mit Grad 2 N2 ist, dann ist N0=N2+1(4) Die Tiefe eines vollständigen Binärbaums mit n Knoten ist

(Hinweis: [ ] bedeutet Abrunden)

Empfohlene Kurse:

PHP-Tutorial.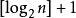

(5) Wenn jeder Knoten eines vollständigen Binärbaums mit N Knoten sequentiell gespeichert wird, haben die Knoten die folgende Beziehung: Wenn I die Knotennummer ist, dann ist I> ;1, dann ist die Nummer seines übergeordneten Knotens I/2;

Wenn 2*I<=N, dann ist die Nummer seines linken untergeordneten Knotens (d. h. des Wurzelknotens des linken Teilbaums) 2 *I; Wenn 2*I>N, dann gibt es kein linkes Kind.

Wenn 2*I+1<=N, dann ist die Knotennummer seines rechten Kindes 2*I+1; *I+1> N, dann gibt es kein richtiges Kind.

(6) Bei N Knoten können h(N) verschiedene Binärbäume gebildet werden.

h(N) ist der N-te Term der Cattelan-Zahl. h(n)=C(2*n,n)/(n+1).

(7) Es gibt i Verzweigungspunkte, I ist die Summe der Straßenlängen aller Verzweigungspunkte, J ist die Summe der Straßenlängen der Blätter J=I+2i [2]

Grundkonzepte

Binärbäume werden rekursiv definiert und ihre Knoten sind in linke und rechte Teilbäume unterteilt. Logischerweise haben Binärbäume fünf Grundformen: ( 1) Leerer Binärbaum – wie in Abbildung (a);

(2) Ein Binärbaum mit nur einem Wurzelknoten – wie in (b) gezeigt; Teilbaum – wie in (c) gezeigt;

(4) Nur der rechte Teilbaum – wie in Abbildung (d) gezeigt; (5) Vollständiger Binärbaum – wie in (e) gezeigt .

Hinweis: Obwohl Binärbäume viele Ähnlichkeiten mit Bäumen haben, sind Binärbäume kein Sonderfall von Bäumen. [1]

Typ

(1) Vollständiger Binärbaum – wenn die Höhe des Binärbaums h ist, mit Ausnahme der h-ten Ebene alle anderen Ebenen (1~h -1) Die Anzahl der Knoten hat die maximale Anzahl erreicht. Es gibt Blattknoten in Schicht h, und die Blattknoten sind von links nach rechts angeordnet.

(2) Vollständiger Binärbaum – ein Binärbaum, in dem jeder Knoten außer den Blattknoten linke und rechte Unterblätter hat und die Blattknoten alle unten liegen.

(3) Ausgeglichener Binärbaum – Ein ausgeglichener Binärbaum wird auch AVL-Baum genannt (im Gegensatz zum AVL-Algorithmus). Er ist ein binärer Sortierbaum und hat die folgenden Eigenschaften: Er ist ein leerer Baum oder es Der absolute Wert des Höhenunterschieds zwischen dem linken und dem rechten Teilbaum überschreitet nicht 1, und der linke und der rechte Teilbaum sind beide ausgeglichene Binärbäume.

Diskriminierung

Binärbaum ist kein Sonderfall von Baum. Obwohl er viele Ähnlichkeiten mit Baum aufweist, gibt es zwei Hauptunterschiede zwischen Baum und Binärbaum:

1. Es gibt keine Begrenzung für den maximalen Grad eines Knotens in einem Baum, während der maximale Grad eines binären Baumknotens 2 ist Knoten eines Baums, während die Knoten eines Binärbaums links und rechts sind.

Das obige ist der detaillierte Inhalt vonGrundlegende Eigenschaften von Binärbäumen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!