Die zeitliche und räumliche Komplexität des Algorithmus
Die Komplexität des Algorithmus bezieht sich auf die Ressourcen, die zum Ausführen des Algorithmus erforderlich sind, nachdem er in ein ausführbares Programm geschrieben wurde. Zu den Ressourcen gehören Zeitressourcen und Speicherressourcen. Anwendungen zur Einführung in Mathematik und Informatik.

Definition der Zeitkomplexität des Algorithmus: (Empfohlenes Lernen: PHP-Video-Tutorial)
In Bearbeitung Während Bei der Algorithmusanalyse ist die Gesamtzahl der Anweisungsausführungen T(n) eine Funktion der Problemgröße n, und dann wird die Änderung von T(n) mit n analysiert und die Größenordnung von T(n) bestimmt. Die Zeitkomplexität des Algorithmus, also die Zeitmessung des Algorithmus, wird wie folgt geschrieben: T(n) = O(f(n)). Dies bedeutet, dass mit zunehmender Problemgröße n die Wachstumsrate der Ausführungszeit des Algorithmus mit der Wachstumsrate von f (n) übereinstimmt, was als asymptotische Zeitkomplexität des Algorithmus bezeichnet wird, die als Zeitkomplexität bezeichnet wird. wobei f(n) eine Funktion der Problemgröße n ist.
Verwenden Sie den Großbuchstaben O(), um die zeitliche Komplexität des Algorithmus widerzuspiegeln, die wir Big-O-Notation nennen.
Wenn in verschiedenen Algorithmen die Anzahl der Anweisungsausführungen im Algorithmus konstant ist, beträgt die Zeitkomplexität O (1). Wenn die Zeithäufigkeit unterschiedlich ist, kann die Zeitkomplexität außerdem gleich sein. Beispielsweise haben T(n)=n^2+3n+4 und T(n)=4n^2+2n+1 unterschiedliche Frequenzen, aber die zeitliche Komplexität ist gleich, beide sind O(n^2).
In aufsteigender Reihenfolge angeordnet sind häufige Zeitkomplexitäten:
Konstante Ordnung O(1), logarithmische Ordnung O(log2n) (Logarithmus von n mit Basis 2, das Gleiche unten) ) , lineare Ordnung O(n),
lineare logarithmische Ordnung O(nlog2n), quadratische Ordnung O(n^2), kubische Ordnung O(n^3),...,
K-te Potenzordnung O(n^k), Exponentialordnung O(2^n). Mit zunehmender Problemgröße n nimmt die oben genannte Zeitkomplexität weiter zu und die Ausführungseffizienz des Algorithmus wird geringer.
Raumkomplexität des Algorithmus
Ähnlich wie die Zeitkomplexität bezieht sich die Raumkomplexität auf die Messung des Speicherplatzes, der erforderlich ist, wenn ein Algorithmus in einem Computer ausgeführt wird.
wird aufgezeichnet als:
S(n)=O(f(n))
Der während der Algorithmusausführung erforderliche Speicherplatz umfasst 3 Teile :
Der vom Algorithmusprogramm belegte Speicherplatz;
Der von den eingegebenen Anfangsdaten belegte Speicherplatz;
Der zusätzliche Speicherplatz, der während der Ausführung des Algorithmus benötigt wird.
Um den vom Algorithmus belegten Speicherplatz zu reduzieren, wird bei vielen praktischen Problemen üblicherweise die Komprimierungsspeichertechnologie verwendet.
Weitere technische Artikel zum Thema PHP finden Sie in der Spalte PHP-Grafik-Tutorial zum Lernen
Das obige ist der detaillierte Inhalt vonDie zeitliche und räumliche Komplexität des Algorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 CLIP-BEVFormer: Überwacht explizit die BEVFormer-Struktur, um die Leistung der Long-Tail-Erkennung zu verbessern
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Überwacht explizit die BEVFormer-Struktur, um die Leistung der Long-Tail-Erkennung zu verbessern
Mar 26, 2024 pm 12:41 PM
Oben geschrieben und das persönliche Verständnis des Autors: Derzeit spielt das Wahrnehmungsmodul im gesamten autonomen Fahrsystem eine entscheidende Rolle Das Steuermodul im autonomen Fahrsystem trifft zeitnahe und korrekte Urteile und Verhaltensentscheidungen. Derzeit sind Autos mit autonomen Fahrfunktionen in der Regel mit einer Vielzahl von Dateninformationssensoren ausgestattet, darunter Rundumsichtkamerasensoren, Lidar-Sensoren und Millimeterwellenradarsensoren, um Informationen in verschiedenen Modalitäten zu sammeln und so genaue Wahrnehmungsaufgaben zu erfüllen. Der auf reinem Sehen basierende BEV-Wahrnehmungsalgorithmus wird von der Industrie aufgrund seiner geringen Hardwarekosten und einfachen Bereitstellung bevorzugt, und seine Ausgabeergebnisse können problemlos auf verschiedene nachgelagerte Aufgaben angewendet werden.
 Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Zu den häufigsten Herausforderungen, mit denen Algorithmen für maschinelles Lernen in C++ konfrontiert sind, gehören Speicherverwaltung, Multithreading, Leistungsoptimierung und Wartbarkeit. Zu den Lösungen gehören die Verwendung intelligenter Zeiger, moderner Threading-Bibliotheken, SIMD-Anweisungen und Bibliotheken von Drittanbietern sowie die Einhaltung von Codierungsstilrichtlinien und die Verwendung von Automatisierungstools. Praktische Fälle zeigen, wie man die Eigen-Bibliothek nutzt, um lineare Regressionsalgorithmen zu implementieren, den Speicher effektiv zu verwalten und leistungsstarke Matrixoperationen zu nutzen.
 Entdecken Sie die zugrunde liegenden Prinzipien und die Algorithmusauswahl der C++-Sortierfunktion
Apr 02, 2024 pm 05:36 PM
Entdecken Sie die zugrunde liegenden Prinzipien und die Algorithmusauswahl der C++-Sortierfunktion
Apr 02, 2024 pm 05:36 PM
Die unterste Ebene der C++-Sortierfunktion verwendet die Zusammenführungssortierung, ihre Komplexität beträgt O(nlogn) und bietet verschiedene Auswahlmöglichkeiten für Sortieralgorithmen, einschließlich schneller Sortierung, Heap-Sortierung und stabiler Sortierung.
 Kann künstliche Intelligenz Kriminalität vorhersagen? Entdecken Sie die Möglichkeiten von CrimeGPT
Mar 22, 2024 pm 10:10 PM
Kann künstliche Intelligenz Kriminalität vorhersagen? Entdecken Sie die Möglichkeiten von CrimeGPT
Mar 22, 2024 pm 10:10 PM
Die Konvergenz von künstlicher Intelligenz (KI) und Strafverfolgung eröffnet neue Möglichkeiten zur Kriminalprävention und -aufdeckung. Die Vorhersagefähigkeiten künstlicher Intelligenz werden häufig in Systemen wie CrimeGPT (Crime Prediction Technology) genutzt, um kriminelle Aktivitäten vorherzusagen. Dieser Artikel untersucht das Potenzial künstlicher Intelligenz bei der Kriminalitätsvorhersage, ihre aktuellen Anwendungen, die Herausforderungen, denen sie gegenübersteht, und die möglichen ethischen Auswirkungen der Technologie. Künstliche Intelligenz und Kriminalitätsvorhersage: Die Grundlagen CrimeGPT verwendet Algorithmen des maschinellen Lernens, um große Datensätze zu analysieren und Muster zu identifizieren, die vorhersagen können, wo und wann Straftaten wahrscheinlich passieren. Zu diesen Datensätzen gehören historische Kriminalstatistiken, demografische Informationen, Wirtschaftsindikatoren, Wettermuster und mehr. Durch die Identifizierung von Trends, die menschliche Analysten möglicherweise übersehen, kann künstliche Intelligenz Strafverfolgungsbehörden stärken
 Verbesserter Erkennungsalgorithmus: zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern
Jun 06, 2024 pm 12:33 PM
Verbesserter Erkennungsalgorithmus: zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern
Jun 06, 2024 pm 12:33 PM
01Ausblicksübersicht Derzeit ist es schwierig, ein angemessenes Gleichgewicht zwischen Detektionseffizienz und Detektionsergebnissen zu erreichen. Wir haben einen verbesserten YOLOv5-Algorithmus zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern entwickelt, der mehrschichtige Merkmalspyramiden, Multierkennungskopfstrategien und hybride Aufmerksamkeitsmodule verwendet, um die Wirkung des Zielerkennungsnetzwerks in optischen Fernerkundungsbildern zu verbessern. Laut SIMD-Datensatz ist der mAP des neuen Algorithmus 2,2 % besser als YOLOv5 und 8,48 % besser als YOLOX, wodurch ein besseres Gleichgewicht zwischen Erkennungsergebnissen und Geschwindigkeit erreicht wird. 02 Hintergrund und Motivation Mit der rasanten Entwicklung der Fernerkundungstechnologie wurden hochauflösende optische Fernerkundungsbilder verwendet, um viele Objekte auf der Erdoberfläche zu beschreiben, darunter Flugzeuge, Autos, Gebäude usw. Objekterkennung bei der Interpretation von Fernerkundungsbildern
 Üben und denken Sie an die multimodale große Modellplattform DataCanvas von Jiuzhang Yunji
Oct 20, 2023 am 08:45 AM
Üben und denken Sie an die multimodale große Modellplattform DataCanvas von Jiuzhang Yunji
Oct 20, 2023 am 08:45 AM
1. Die historische Entwicklung multimodaler Großmodelle zeigt den ersten Workshop zur künstlichen Intelligenz, der 1956 am Dartmouth College in den Vereinigten Staaten stattfand Pioniere der symbolischen Logik (außer dem Neurobiologen Peter Milner in der Mitte der ersten Reihe). Diese symbolische Logiktheorie konnte jedoch lange Zeit nicht verwirklicht werden und leitete in den 1980er und 1990er Jahren sogar den ersten KI-Winter ein. Erst mit der kürzlich erfolgten Implementierung großer Sprachmodelle haben wir entdeckt, dass neuronale Netze dieses logische Denken tatsächlich tragen. Die Arbeit des Neurobiologen Peter Milner inspirierte die spätere Entwicklung künstlicher neuronaler Netze, und aus diesem Grund wurde er zur Teilnahme eingeladen in diesem Projekt.
 Anwendung von Algorithmen beim Aufbau einer 58-Porträt-Plattform
May 09, 2024 am 09:01 AM
Anwendung von Algorithmen beim Aufbau einer 58-Porträt-Plattform
May 09, 2024 am 09:01 AM
1. Hintergrund des Baus der 58-Portrait-Plattform Zunächst möchte ich Ihnen den Hintergrund des Baus der 58-Portrait-Plattform mitteilen. 1. Das traditionelle Denken der traditionellen Profiling-Plattform reicht nicht mehr aus. Der Aufbau einer Benutzer-Profiling-Plattform basiert auf Data-Warehouse-Modellierungsfunktionen, um Daten aus mehreren Geschäftsbereichen zu integrieren, um genaue Benutzerporträts zu erstellen Und schließlich muss es über Datenplattformfunktionen verfügen, um Benutzerprofildaten effizient zu speichern, abzufragen und zu teilen sowie Profildienste bereitzustellen. Der Hauptunterschied zwischen einer selbst erstellten Business-Profiling-Plattform und einer Middle-Office-Profiling-Plattform besteht darin, dass die selbst erstellte Profiling-Plattform einen einzelnen Geschäftsbereich bedient und bei Bedarf angepasst werden kann. Die Mid-Office-Plattform bedient mehrere Geschäftsbereiche und ist komplex Modellierung und bietet allgemeinere Funktionen. 2.58 Benutzerporträts vom Hintergrund der Porträtkonstruktion im Mittelbahnsteig 58
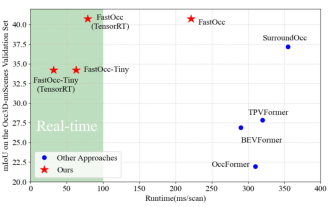 Fügen Sie SOTA in Echtzeit hinzu und explodieren Sie! FastOcc: Schnellere Inferenz und ein einsatzfreundlicher Occ-Algorithmus sind da!
Mar 14, 2024 pm 11:50 PM
Fügen Sie SOTA in Echtzeit hinzu und explodieren Sie! FastOcc: Schnellere Inferenz und ein einsatzfreundlicher Occ-Algorithmus sind da!
Mar 14, 2024 pm 11:50 PM
Oben geschrieben & Das persönliche Verständnis des Autors ist, dass im autonomen Fahrsystem die Wahrnehmungsaufgabe eine entscheidende Komponente des gesamten autonomen Fahrsystems ist. Das Hauptziel der Wahrnehmungsaufgabe besteht darin, autonome Fahrzeuge in die Lage zu versetzen, Umgebungselemente wie auf der Straße fahrende Fahrzeuge, Fußgänger am Straßenrand, während der Fahrt angetroffene Hindernisse, Verkehrszeichen auf der Straße usw. zu verstehen und wahrzunehmen und so flussabwärts zu helfen Module Treffen Sie richtige und vernünftige Entscheidungen und Handlungen. Ein Fahrzeug mit autonomen Fahrfähigkeiten ist in der Regel mit verschiedenen Arten von Informationserfassungssensoren ausgestattet, wie z. B. Rundumsichtkamerasensoren, Lidar-Sensoren, Millimeterwellenradarsensoren usw., um sicherzustellen, dass das autonome Fahrzeug die Umgebung genau wahrnehmen und verstehen kann Elemente, die es autonomen Fahrzeugen ermöglichen, beim autonomen Fahren die richtigen Entscheidungen zu treffen. Kopf





