Binärbaumformeln, die Sie verstehen müssen

1. Eigenschaften allgemeiner Binärbäume
Eigenschaften 1. Auf der i-Ebene eines nicht leeren Binärbaums gibt es höchstens 2^i Knoten .
Eigenschaft 2. In einem Binärbaum mit der Höhe K gibt es höchstens 2^(k+1)-1 Knoten.
Eigenschaft 3. Wenn für jeden nicht leeren Binärbaum die Anzahl der Blattknoten n0 und die Anzahl der Knoten mit Grad 2 n2 beträgt, dann ist n0 = n2 + 1.
2, Vollständiger Binärbaum
Definition: Wenn in einem Binärbaum nur die Grade der Knoten auf den unteren beiden Ebenen kleiner als 2 sind, sind die Grade von Wenn die Knoten auf allen anderen Ebenen gleich 2 sind und die Knoten der unteren Ebene an den Positionen ganz links in der Ebene konzentriert sind, wird dieser Binärbaum als vollständiger Binärbaum bezeichnet.
Eigenschaft 1. Die Höhe k eines vollständigen Binärbaums mit n Knoten beträgt [log^2n].
Eigenschaft 2. Wenn für einen vollständigen Binärbaum mit n Knoten alle Knoten im Binärbaum von oben (Wurzelknoten) nach unten (Blattknoten) und von links nach rechts geordnet sind, beginnt die Nummerierung von 0 bis n-1, dann gibt es für jeden Knoten, dessen Index i ist:
(1) Wenn i=0, dann ist es der Wurzelknoten und er hat keinen übergeordneten Knoten; wenn i>0, dann Der Index seines übergeordneten Knotens ist (i-1)/2.
(2) Wenn 2i+1<=n-1, dann ist der Index des linken untergeordneten Knotens des Knotens mit dem Index i 2i+1; andernfalls hat der Knoten mit dem Index i keinen linken untergeordneten Knoten Knoten.
(3) Wenn 2i+2<=n-1, dann ist der Index des rechten untergeordneten Knotens des Knotens mit dem Index i 2i+2; andernfalls hat der Knoten mit dem Index i kein rechtes Kind Knoten.
3. Vollständiger Binärbaum
Definition: Wenn ein Knoten eines Binärbaums entweder ein Blatt ist oder zwei nicht leere Teilbäume hat, dann ist es dieser Binärbaum namens Vollständiger Binärbaum.
Eigenschaft: In einem vollständigen Binärbaum ist die Anzahl der Blattknoten um 1 größer als die Anzahl der Verzweigungsknoten.
4. Erweiterter Binärbaum
Definition: Ein erweiterter Binärbaum ist eine Erweiterung eines vorhandenen Binärbaums. Nach der Erweiterung werden die Knoten des ursprünglichen Binärbaums zu Zweigen mit Grad 2. Knoten. Das heißt, wenn der Grad des ursprünglichen Knotens 2 ist, bleibt er unverändert; wenn der Grad 1 ist, wird ein Zweig hinzugefügt, wenn der Grad 0 ist, werden zwei Zweige hinzugefügt.
Eigenschaft 1. In einem erweiterten Binärbaum ist die Anzahl der externen Knoten um 1 größer als die Anzahl der internen Knoten.
Eigenschaft 2. Für jeden erweiterten Binärbaum ist die folgende Beziehung zwischen der externen Pfadlänge E und der internen Pfadlänge I erfüllt: E=I+2n, wobei n die Anzahl der internen Knoten ist.
Weitere technische Artikel zu häufig gestellten Fragen finden Sie in der Spalte FAQ mehr!
Das obige ist der detaillierte Inhalt vonBinärbaumformeln, die Sie verstehen müssen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1377
1377
 52
52
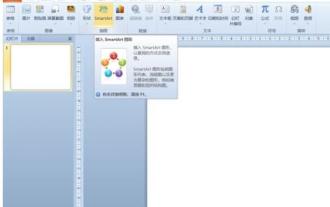 Detaillierte Methode zum Einfügen eines Formeleffekt-Flussdiagramms in PPT
Mar 26, 2024 pm 04:36 PM
Detaillierte Methode zum Einfügen eines Formeleffekt-Flussdiagramms in PPT
Mar 26, 2024 pm 04:36 PM
1. Öffnen Sie PPT, klicken Sie auf die Registerkarte [Einfügen] und dann auf die Schaltfläche [smartArt] in der Gruppe [Illustrationen]. 2. Klicken Sie im sich öffnenden Dialogfeld [SmartArt-Grafiken auswählen] auf [Verarbeiten]. 3. Wählen Sie im sich öffnenden Bereich [Prozess] das Flussdiagramm [Formel] aus. 4. Klicken Sie auf [OK] und das Flussdiagramm [Formel] wird in den Folienbereich eingefügt. 5. Klicken Sie in der Spalte [Text hier eingeben] auf [Text] oder klicken Sie in der Grafik auf [Text], um Inhalt einzugeben. 6. Wählen Sie die Form in der Grafik aus, klicken Sie auf die Registerkarte [Design] von [smartArt Tools] und klicken Sie auf die Schaltfläche [Form hinzufügen] in der Gruppe [Grafiken erstellen], um eine Form hinzuzufügen. 7. Die Formen in den Grafiken können auch ausgewählt und gelöscht werden. Natürlich können Sie sie bei Bedarf auch in Smar löschen.
 So bedienen Sie Excel-Tabellenformeln
Mar 20, 2024 pm 12:07 PM
So bedienen Sie Excel-Tabellenformeln
Mar 20, 2024 pm 12:07 PM
Wenn Sie Excel-Software am Arbeitsplatz verwenden, werden häufig Funktionsformeln verwendet. Wenn Sie Excel beherrschen möchten, müssen Sie sich mit der Bedienung von Funktionsformeln auskennen. Es ist eigentlich nicht schwer, mit den einfachsten Formeln zu lernen. Heute werde ich mit Ihnen teilen, wie man Excel-Tabellenformeln bedient. Lassen Sie uns mit Ihnen lernen. 1. Öffnen Sie zunächst Excel. Da ich hier eine Demonstration mache, gebe ich zufällig zwei Datensätze ein. Jetzt müssen wir das Produkt dieser beiden Datensätze berechnen. Wir möchten das Produkt der Spalten A und B berechnen und die Zelle bei D4 platzieren, wie im roten Kreis in der Abbildung unten gezeigt: 2. Geben Sie dann das Gleichheitszeichen in die Zelle ein und wählen Sie den ersten Parameter Zelle B4 aus, Enter das Multiplikationszeichen und wählen Sie den zweiten Parameter C4
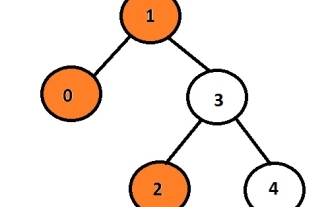 Drucken Sie die linke Ansicht des Binärbaums in C-Sprache
Sep 03, 2023 pm 01:25 PM
Drucken Sie die linke Ansicht des Binärbaums in C-Sprache
Sep 03, 2023 pm 01:25 PM
Die Aufgabe besteht darin, den linken Knoten des angegebenen Binärbaums zu drucken. Zuerst fügt der Benutzer Daten ein, wodurch ein Binärbaum erstellt wird, und druckt dann die linke Ansicht des resultierenden Baums aus. Jeder Knoten kann höchstens 2 untergeordnete Knoten haben, sodass dieses Programm nur über den mit dem Knoten verknüpften linken Zeiger iterieren darf. Wenn der linke Zeiger nicht null ist, bedeutet dies, dass ihm einige Daten oder ein Zeiger zugeordnet sind, andernfalls wird er als gedruckt und angezeigt das linke untergeordnete Element der Ausgabe. BeispielEingabe:10324Ausgabe:102Hier repräsentiert der orangefarbene Knoten die linke Ansicht des Binärbaums. In der angegebenen Grafik ist der Knoten mit den Daten 1 der Wurzelknoten, daher wird er gedruckt und anstatt zum linken untergeordneten Knoten zu gehen, wird er 0 drucken und dann geht er zu 3 und gibt seinen linken untergeordneten Knoten aus, der 2 ist. Wir können eine rekursive Methode verwenden, um die Knotenebene zu speichern
 Detaillierte Erläuterung der binären Baumstruktur in Java
Jun 16, 2023 am 08:58 AM
Detaillierte Erläuterung der binären Baumstruktur in Java
Jun 16, 2023 am 08:58 AM
Binärbäume sind eine gängige Datenstruktur in der Informatik und eine häufig verwendete Datenstruktur in der Java-Programmierung. In diesem Artikel wird die Binärbaumstruktur in Java ausführlich vorgestellt. 1. Was ist ein Binärbaum? In der Informatik ist ein Binärbaum eine Baumstruktur, in der jeder Knoten höchstens zwei untergeordnete Knoten hat. Unter diesen ist der linke untergeordnete Knoten kleiner als der übergeordnete Knoten und der rechte untergeordnete Knoten größer als der übergeordnete Knoten. In der Java-Programmierung werden Binärbäume häufig verwendet, um das Sortieren und Suchen darzustellen und die Effizienz der Datenabfrage zu verbessern. 2. Implementierung eines Binärbaums in Java In Java ein Binärbaum
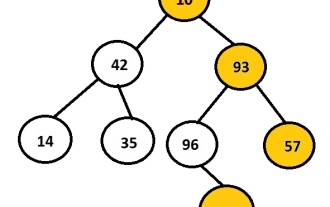 Drucken Sie in der Sprache C die rechte Ansicht des Binärbaums
Sep 16, 2023 pm 11:13 PM
Drucken Sie in der Sprache C die rechte Ansicht des Binärbaums
Sep 16, 2023 pm 11:13 PM
Die Aufgabe besteht darin, den rechten Knoten des angegebenen Binärbaums zu drucken. Zuerst fügt der Benutzer Daten ein, um einen Binärbaum zu erstellen, und druckt dann eine rechte Ansicht des resultierenden Baums. Das Bild oben zeigt einen Binärbaum, der mit den Knoten 10, 42, 93, 14, 35, 96, 57 und 88 erstellt wurde, wobei die Knoten auf der rechten Seite des Baums ausgewählt und angezeigt werden. Beispielsweise sind 10, 93, 57 und 88 die Knoten ganz rechts im Binärbaum. Beispieleingabe: 1042931435965788 Ausgabe: 10935788 Jeder Knoten hat zwei Zeiger, den linken Zeiger und den rechten Zeiger. Gemäß dieser Frage muss das Programm nur den richtigen Knoten durchlaufen. Daher muss das linke Kind des Knotens nicht berücksichtigt werden. In der rechten Ansicht werden alle Knoten gespeichert, die der letzte Knoten in ihrer Hierarchie sind. Deshalb können wir
 So implementieren Sie die Binärbaum-Traversierung mit Python
Jun 09, 2023 pm 09:12 PM
So implementieren Sie die Binärbaum-Traversierung mit Python
Jun 09, 2023 pm 09:12 PM
Als häufig verwendete Datenstruktur werden Binärbäume häufig zum Speichern, Suchen und Sortieren von Daten verwendet. Das Durchlaufen eines Binärbaums ist eine der häufigsten Operationen. Als einfache und benutzerfreundliche Programmiersprache verfügt Python über viele Methoden zur Implementierung der Binärbaumdurchquerung. In diesem Artikel wird erläutert, wie Sie mit Python die Durchquerung eines Binärbaums vor, in der Reihenfolge und nach der Bestellung implementieren. Grundlagen von Binärbäumen Bevor wir lernen, wie man einen Binärbaum durchläuft, müssen wir die Grundkonzepte eines Binärbaums verstehen. Ein Binärbaum besteht aus Knoten, jeder Knoten hat einen Wert und zwei untergeordnete Knoten (linker untergeordneter Knoten und rechter untergeordneter Knoten).
 So verwenden Sie die Formelsuche
Feb 19, 2024 pm 10:37 PM
So verwenden Sie die Formelsuche
Feb 19, 2024 pm 10:37 PM
Die Formel SVERWEIS ist eine sehr häufig verwendete Funktion in Microsoft Excel. Sie wird verwendet, um einen bestimmten Wert in einer Tabelle oder einem Datensatz zu finden und andere damit verbundene Werte zurückzugeben. In diesem Artikel erfahren Sie, wie Sie die VLOOKUP-Formel richtig verwenden. Die grundlegende Syntax der VLOOKUP-Funktion lautet wie folgt: VLOOKUP(lookup_value, table_array, col_index_num, [range_lookup]) wobei: lookup
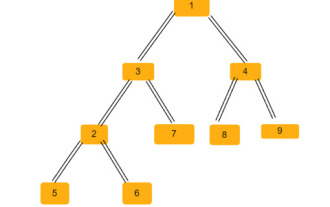 Die Anzahl gleichschenkliger Dreiecke in einem Binärbaum
Sep 05, 2023 am 09:41 AM
Die Anzahl gleichschenkliger Dreiecke in einem Binärbaum
Sep 05, 2023 am 09:41 AM
Ein Binärbaum ist eine Datenstruktur, in der jeder Knoten bis zu zwei untergeordnete Knoten haben kann. Diese Kinder werden linke Kinder bzw. rechte Kinder genannt. Angenommen, wir erhalten eine übergeordnete Array-Darstellung, Sie müssen diese verwenden, um einen Binärbaum zu erstellen. Ein Binärbaum kann mehrere gleichschenklige Dreiecke haben. Wir müssen die Gesamtzahl der möglichen gleichschenkligen Dreiecke in diesem Binärbaum ermitteln. In diesem Artikel werden wir verschiedene Techniken zur Lösung dieses Problems in C++ untersuchen. Wenn Sie das Problem verstehen, erhalten Sie ein übergeordnetes Array. Sie müssen es in Form eines Binärbaums darstellen, sodass der Array-Index den Wert des Baumknotens bildet und der Wert im Array den übergeordneten Knoten dieses bestimmten Index angibt. Beachten Sie, dass -1 immer das Root-Elternteil ist. Nachfolgend finden Sie ein Array und seine binäre Baumdarstellung. Parentarray=[0,-1,3,1,



