So implementieren Sie Canopy-Clustering in Python

Der Canopy-Algorithmus wurde im Jahr 2000 von Andrew McCallum, Kamal Nigam und Lyle Ungar vorgeschlagen. Es handelt sich um eine Vorverarbeitung des k-Means-Clustering-Algorithmus und des hierarchischen Clustering-Algorithmus. Wie wir alle wissen, besteht einer der Nachteile von kmeans darin, dass der k-Wert manuell angepasst werden muss. Der k-Wert kann später mithilfe der Ellbogenmethode und des Silhouette-Koeffizienten endgültig bestimmt werden. Diese Methoden werden jedoch „ex post facto“ beurteilt. Die Rolle des Canopy-Algorithmus besteht darin, dass er die anfängliche Anzahl von Clusterzentren und Clusterzentren für den K-Means-Algorithmus durch grobes Clustering im Voraus bestimmt.

Verwendetes Paket:

import math
import random
import numpy as np
from datetime import datetime
from pprint import pprint as p
import matplotlib.pyplot as plt

1 Darstellung auf einer zweidimensionalen Ebene) Datendatensatz.

Natürlich können auch hochdimensionale Daten verwendet werden, und ich habe den Canopy-Core-Algorithmus in die Klasse geschrieben. Später können Daten jeder Dimension durch direkte Aufrufe verarbeitet werden, natürlich nur in kleinen Batches können große Datenmengen nach Mahout und Hadoop verschoben werden.

# 随机生成500个二维[0,1)平面点
dataset = np.random.rand(500, 2)

Verwandte Empfehlungen: „Python-Video-Tutorial“

2. Die Attribute der Klassen sind dann wie folgt:

class Canopy:
    def __init__(self, dataset):        
        self.dataset = dataset        
        self.t1 = 0
      self.t2 = 0

Fügen Sie die Einstellung der Anfangswerte von t1 und t2 und der Größenfunktion hinzu

   # 设置初始阈值  
def setThreshold(self, t1, t2):        
    if t1 > t2:
        self.t1 = t1            
        self.t2 = t2        
    else:
        print('t1 needs to be larger than t2!')

3. Die Entfernungsberechnungsmethode zwischen jedem Mittelpunkt ist die euklidische Entfernung .

#使用欧式距离进行距离的计算
def euclideanDistance(self, vec1, vec2):        
    return math.sqrt(((vec1 - vec2)**2).sum())

4. Schreiben Sie dann eine Funktion, die zufällig Indizes aus dem Datensatz entsprechend der Länge des Datensatzes auswählt

# 根据当前dataset的长度随机选择一个下标 
def getRandIndex(self):        
    return random.randint(0, len(self.dataset) - 1)

Kernalgorithmus

def clustering(self):        
        if self.t1 == 0:
            print('Please set the threshold.')        
        else:
            canopies = []  # 用于存放最终归类结果
            while len(self.dataset) != 0:
                rand_index = self.getRandIndex()
                current_center = self.dataset[rand_index]  # 随机获取一个中心点，定为P点
                current_center_list = []  # 初始化P点的canopy类容器
                delete_list = []  # 初始化P点的删除容器
                self.dataset = np.delete(                    
                     self.dataset, rand_index, 0)  # 删除随机选择的中心点P
                for datum_j in range(len(self.dataset)):
                    datum = self.dataset[datum_j]
                    distance = self.euclideanDistance(
                        current_center, datum)  # 计算选取的中心点P到每个点之间的距离
                    if distance < self.t1:
                        # 若距离小于t1，则将点归入P点的canopy类
                        current_center_list.append(datum)                    
                    if distance < self.t2:
                        delete_list.append(datum_j)  # 若小于t2则归入删除容器
                # 根据删除容器的下标，将元素从数据集中删除
                self.dataset = np.delete(self.dataset, delete_list, 0)
                canopies.append((current_center, current_center_list))        
          return canopies

Um die spätere Datenvisualisierung zu erleichtern, sind die hier definierten Canopies ein Array. Natürlich kann auch dict verwendet werden.
6.main()-Funktion

def main():
    t1 = 0.6
    t2 = 0.4
    gc = Canopy(dataset)
    gc.setThreshold(t1, t2)
    canopies = gc.clustering()
    print('Get %s initial centers.' % len(canopies))    
    #showCanopy(canopies, dataset, t1, t2)

Canopy-Clustering-Visualisierungscode

def showCanopy(canopies, dataset, t1, t2):
    fig = plt.figure()
    sc = fig.add_subplot(111)
    colors = ['brown', 'green', 'blue', 'y', 'r', 'tan', 'dodgerblue', 'deeppink', 'orangered', 'peru', 'blue', 'y', 'r',              'gold', 'dimgray', 'darkorange', 'peru', 'blue', 'y', 'r', 'cyan', 'tan', 'orchid', 'peru', 'blue', 'y', 'r', 'sienna']
    markers = [&#39;*&#39;, &#39;h&#39;, &#39;H&#39;, &#39;+&#39;, &#39;o&#39;, &#39;1&#39;, &#39;2&#39;, &#39;3&#39;, &#39;,&#39;, &#39;v&#39;, &#39;H&#39;, &#39;+&#39;, &#39;1&#39;, &#39;2&#39;, &#39;^&#39;,               &#39;<&#39;, &#39;>&#39;, &#39;.&#39;, &#39;4&#39;, &#39;H&#39;, &#39;+&#39;, &#39;1&#39;, &#39;2&#39;, &#39;s&#39;, &#39;p&#39;, &#39;x&#39;, &#39;D&#39;, &#39;d&#39;, &#39;|&#39;, &#39;_&#39;]    for i in range(len(canopies)):
        canopy = canopies[i]
        center = canopy[0]
        components = canopy[1]
        sc.plot(center[0], center[1], marker=markers[i],
                color=colors[i], markersize=10)
        t1_circle = plt.Circle(
            xy=(center[0], center[1]), radius=t1, color=&#39;dodgerblue&#39;, fill=False)
        t2_circle = plt.Circle(
            xy=(center[0], center[1]), radius=t2, color=&#39;skyblue&#39;, alpha=0.2)
        sc.add_artist(t1_circle)
        sc.add_artist(t2_circle)        for component in components:
            sc.plot(component[0], component[1],
                    marker=markers[i], color=colors[i], markersize=1.5)
    maxvalue = np.amax(dataset)
    minvalue = np.amin(dataset)
    plt.xlim(minvalue - t1, maxvalue + t1)
    plt.ylim(minvalue - t1, maxvalue + t1)
    plt.show()

Das Rendering ist wie folgt:

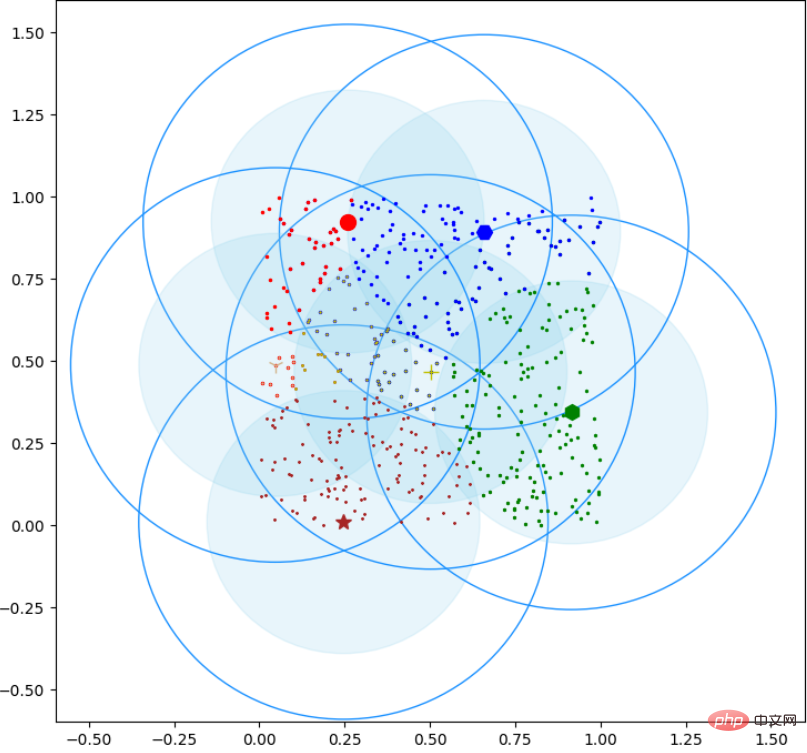
Das obige ist der detaillierte Inhalt vonSo implementieren Sie Canopy-Clustering in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!