

1. Anfängliche Rekursion
Rekursive Funktion: Aufruf der Funktion selbst innerhalb einer Funktion.
Maximale Rekursionstiefe: 998
Wie Sie gerade gesehen haben, wird die rekursive Funktion weiterhin ausgeführt, sofern sie nicht durch äußere Kräfte blockiert wird. Aber wir haben bereits über das Problem von Funktionsaufrufen gesprochen. Jeder Funktionsaufruf generiert einen eigenen Namensraum. Wenn er kontinuierlich aufgerufen wird, führt dies dazu, dass der Namensraum zu viel Speicher belegt, was Python versucht Machen Sie diesem Phänomen ein Ende, die Anzahl der Rekursionsebenen wird zwangsweise auf 997 kontrolliert (solange 997! Sie können keine Verluste erleiden, Sie können sich nicht täuschen lassen ...). verwendet werden, um diese „998-Theorie“ zu beweisen? Hier können wir ein Experiment durchführen:
def foo(n):
print(n)
n += 1
foo(n)
foo(1)Daraus können wir ersehen, dass die maximale Anzahl, die angezeigt werden kann, bevor ein Fehler gemeldet wird, 998 beträgt. Natürlich ist 997 eine von Python für die Speicheroptimierung festgelegte Zahl Unser Programm. Natürlich können wir ihn auf irgendeine Weise ändern:
import sys print(sys.setrecursionlimit(100000))
Wir können die maximale Rekursionstiefe auf diese Weise ändern. Wir setzen einfach die von Python zulässige Rekursionstiefe Die tatsächlich erreichbare Rekursionstiefe hängt von der Leistung des Computers ab. Wir empfehlen jedoch immer noch nicht, diese Standard-Rekursionstiefe zu ändern, denn wenn das Problem nicht mit 997 Rekursionsstufen gelöst werden kann, ist es entweder nicht geeignet, es mit Rekursion zu lösen, oder Ihr Code ist zu schlecht geschrieben~~~
An diesem Punkt haben Sie möglicherweise das Gefühl, dass Rekursion keine so gute Sache und nicht so nützlich ist wie während True! Allerdings kursiert in der Welt ein Sprichwort: Menschen verstehen Zyklen, Götter verstehen Rekursion. Unterschätzen Sie also nicht rekursive Funktionen, weil sie die wahre Bedeutung der Rekursion nicht verstanden haben. Und viele der Algorithmen, die wir in Zukunft lernen werden, werden mit Rekursion zusammenhängen. Komm schon, nur wenn du es lernst, wirst du das Kapital haben, es nicht zu mögen!
2. Rekursionsbeispiel Hier geben wir ein weiteres Beispiel, um zu veranschaulichen, was Rekursion bewirken kann.
Beispiel 1:
Jetzt fragen Sie mich, wie alt ist Herr Alex? Ich sagte, ich verrate es dir nicht, aber Alex ist zwei Jahre älter als Egon.
Wenn du wissen willst, wie alt Alex ist, musst du Egon fragen? Egon sagte: „Ich werde es dir auch nicht sagen, aber ich bin zwei Jahre älter als Sir Wu.“
Sie haben Sir Wu noch einmal gefragt, aber Sir Wu hat es Ihnen auch nicht gesagt. Er sagte, er sei zwei Jahre älter als Taibai.
Dann fragst du Taibai, Taibai wird dir sagen, dass er 18 ist.
Wussten Sie es zu diesem Zeitpunkt? Wie alt ist Alex?
你为什么能知道的?
首先,你是不是问alex的年龄,结果又找到egon、武sir、太白,你挨个儿问过去,一直到拿到一个确切的答案,然后顺着这条线再找回来,才得到最终alex的年龄。这个过程已经非常接近递归的思想。我们就来具体的我分析一下,这几个人之间的规律。
age(4) = age(3) + 2 age(3) = age(2) + 2 age(2) = age(1) + 2 age(1) = 40
那这样的情况,我们的函数怎么写呢?
def age(n):
if n == 1:
return 40
else:
return age(n-1)+2print(age(4))如果有这样一个列表,让你从这个列表中找到66的位置,你要怎么做?
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
你说,so easy!
l.index(66)...
我们之所以用index方法可以找到,是因为python帮我们实现了查找方法。如果,index方法不给你用了。。。你还能找到这个66么?
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
i = 0for num in l: if num == 66:
print(i)
i+=1上面这个方法就实现了从一个列表中找到66所在的位置了。
但我们现在是怎么找到这个数的呀?是不是循环这个列表,一个一个的找的呀?假如我们这个列表特别长,里面好好几十万个数,那我们找一个数如果运气不好的话是不是要对比十几万次?这样效率太低了,我们得想一个新办法。
二分查找算法
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
你观察这个列表,这是不是一个从小到大排序的有序列表呀?
如果这样,假如我要找的数比列表中间的数还大,是不是我直接在列表的后半边找就行了?
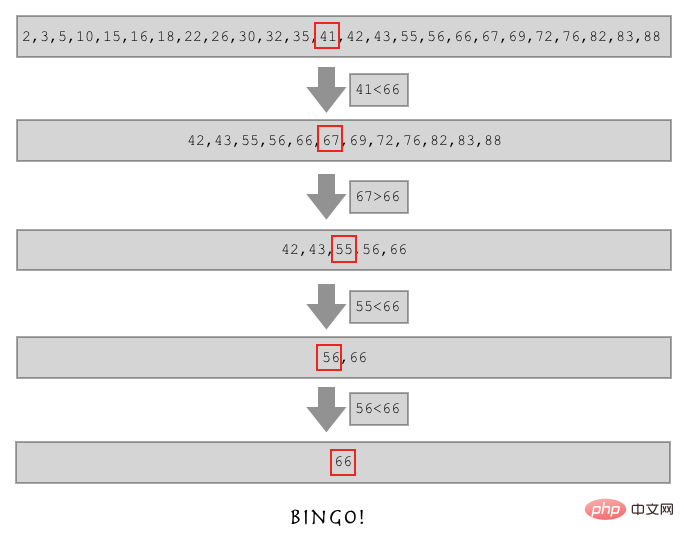
这就是二分查找算法!
那么落实到代码上我们应该怎么实现呢?
简单版二分法
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]def func(l,aim):
mid = (len(l)-1)//2
if l: if aim > l[mid]:
func(l[mid+1:],aim) elif aim < l[mid]:
func(l[:mid],aim) elif aim == l[mid]:
print("bingo",mid) else:
print('找不到')
func(l,66)
func(l,6)升级版二分法
l1 = [1, 2, 4, 5, 7, 9]
def two_search(l,aim,start=0,end=None):
end = len(l)-1 if end is None else end
mid_index = (end - start) // 2 + start
if end >= start:
if aim > l[mid_index]:
return two_search(l,aim,start=mid_index+1,end=end
elif aim < l[mid_index]:
return two_search(l,aim,start=start,end=mid_index-1)
elif aim == l[mid_index]:
return mid_index
else:
return '没有此值'
else:
return '没有此值'
print(two_search(l1,9))Das obige ist der detaillierte Inhalt vonRekursive Python-Funktion, Einführung in den binären Suchalgorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!