
Im vorherigen Artikel wurde kurz das Datenmodell verschachtelter Sammlungen und die Abfragemethode Portal vorgestellt: Baumdatenstruktur-Speichermethode (Abfrage)
Erstellen
Im verschachtelten Sammlungsmodell sind alle Daten tatsächlich ein Knoten, und jeder Knoten belegt 2 Bitwerte. Beginnen wir beispielsweise mit dem Hinzufügen eines Knotens der ersten Ebene für Smartphones.
INSERT INTO `categories` (`title`, `lft`, `rgt`) VALUES('Smartphones', 1, 2);
Smartphones Als Master-Knoten (Root) muss sein LFT 1 sein, und der Wert von rgt erhöht sich, wenn die Anzahl der untergeordneten Elemente in seiner Sammlung zunimmt.
Jetzt möchten wir ein untergeordnetes Android-Element in Smartphones hinzufügen. Verwenden Sie gespeicherte MySQL-Prozeduren.
LOCK TABLE categories WRITE; SELECT @root_left := lft FROM categories WHERE title = 'Smartphones'; UPDATE categories SET rgt = rgt + 2 WHERE rgt > @root_left; UPDATE categories SET lft = lft + 2 WHERE lft > @root_left; INSERT INTO categories (title, lft, rgt) VALUES('Android', @root_left + 1, @root_left + 2); UNLOCK TABLES; SELECT `title`, `lft`, `rgt` FROM `categories`; +-------------+-----+-----+ | title | lft | rgt | +-------------+-----+-----+ | Smartphones | 1 | 4 | | Android | 2 | 3 | +-------------+-----+-----+
Wir versuchen erneut, ein Unterelement Xiaomi zu Android hinzuzufügen:
LOCK TABLE categories WRITE; SELECT @root_left := lft FROM categories WHERE title = 'Android'; UPDATE categories SET rgt = rgt + 2 WHERE rgt > @root_left; UPDATE categories SET lft = lft + 2 WHERE lft > @root_left; INSERT INTO categories (title, lft, rgt) VALUES('小米', @root_left + 1, @root_left + 2); UNLOCK TABLES; SELECT `title`, `lft`, `rgt` FROM `categories`; +-------------+-----+-----+ | title | lft | rgt | +-------------+-----+-----+ | Smartphones | 1 | 6 | | Android | 2 | 5 | | 小米 | 3 | 4 | +-------------+-----+-----+
Zu diesem Zeitpunkt versuchen wir, ein Unterelement iOS zu Smartphones hinzuzufügen. Zuvor haben wir es innen hinzugefügt Ein Android-Element, daher müssen wir hier die gespeicherte Prozedur anpassen und iOS rechts von Android einfügen kann tatsächlich als der umgekehrte Prozess des Hinzufügens neuer Knoten angesehen werden. Wir führen eine Breite ein, um die Breite des Knotens zu messen, die ausgedrückt wird als: rgt - lft + 1. Wir können die gespeicherte Prozedur also wie folgt schreiben:
LOCK TABLE categories WRITE; SELECT @next_right := rgt FROM categories WHERE title = 'Android'; UPDATE categories SET rgt = rgt + 2 WHERE rgt > @next_right; UPDATE categories SET lft = lft + 2 WHERE lft > @next_right; INSERT INTO categories(title, lft, rgt) VALUES('iOS', @next_right + 1, @next_right + 2); UNLOCK TABLES; SELECT `title`, `lft`, `rgt` FROM `categories`; +-------------+-----+-----+ | title | lft | rgt | +-------------+-----+-----+ | Smartphones | 1 | 8 | | Android | 2 | 5 | | 小米 | 3 | 4 | | iOS | 6 | 7 | +-------------+-----+-----+
Update
Das Verschieben von Knoten ist ein relativ komplizierter Vorgang. In der Abbildung unten sollte macOS beispielsweise der Kategorie Unix zugeordnet werden.
Um den Knoten zu verschieben, sind drei Schritte erforderlich:
1. Nehmen Sie den zu verschiebenden Knoten heraus
2 und rgt-Parameter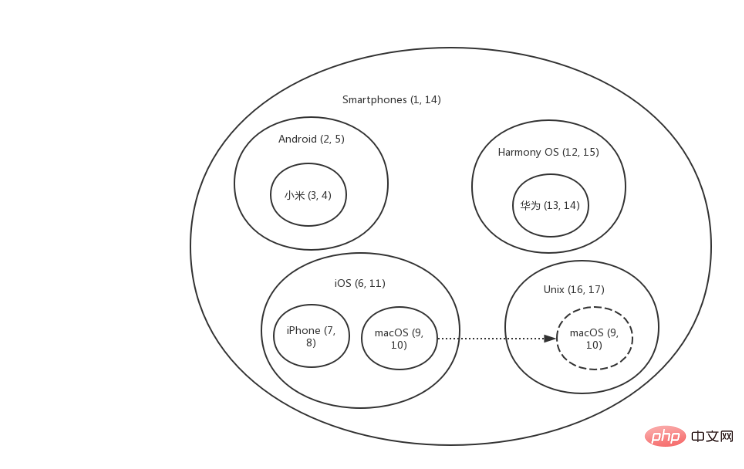
LOCK TABLE categories WRITE; SELECT @delete_left := lft, @delete_right := rgt, @delete_width := rgt - lft + 1 FROM categories WHERE title = 'Android'; DELETE FROM categories WHERE lft BETWEEN @delete_left AND @delete_right; UPDATE categories SET rgt = rgt - @delete_width WHERE rgt > @delete_right; UPDATE categories SET lft = lft - @delete_width WHERE lft > @delete_right; UNLOCK TABLES; SELECT `title`, `lft`, `rgt` FROM `categories`; +-------------+-----+-----+ | title | lft | rgt | +-------------+-----+-----+ | Smartphones | 1 | 4 | | iOS | 2 | 3 | +-------------+-----+-----+
Zusammenfassung
Tatsächlich hat das Datenmodell verschachtelter Sammlungen in SQL Seit langem vorgeschlagen, gibt es viele Pakete, die diese Funktion implementiert haben, wie z. B. laravel-nestedset oder django-mpttFür den Produktionsgebrauch gibt es definitiv kein so einfaches Tabellenstrukturdesign oder sogar andere Optimierungen , wie zum Beispiel ein sogenanntes Es handelt sich um ein geschlossenes Tabellendatenmodell, das in dieser Artikelserie jedem vorgestellt werden sollte.Das obige ist der detaillierte Inhalt vonBaumdatenstruktur-Speichermethode (CUD). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!