Wie hoch ist die zeitliche Komplexität eines rekursiven Algorithmus?

Die zeitliche Komplexität des rekursiven Algorithmus beträgt: [T(n)=o(f(n))], was bedeutet, dass mit zunehmender Problemgröße n die Ausführungszeitwachstumsrate des Algorithmus und f zunimmt (n) Die Wachstumsrate ist proportional zur Wachstumsrate, die als asymptotische Zeitkomplexität des Algorithmus bezeichnet wird.

Zeitkomplexität des rekursiven Algorithmus

Zeitkomplexität:

Im Allgemeinen ist die Anzahl der Wiederholungen grundlegender Operationen im Algorithmus eine Funktion f(n) der Problemgröße n. Analysieren Sie dann die Änderung von f(n) mit n und bestimmen Sie die Größenordnung von T(n). „o“ wird hier verwendet, um die Größenordnung darzustellen und die zeitliche Komplexität des Algorithmus anzugeben.

T(n)=o(f(n));

Das bedeutet, dass mit zunehmender Problemgröße n die Wachstumsrate der Ausführungszeit des Algorithmus proportional zur Wachstumsrate von ist f(n) , was als asymptotische Zeitkomplexität des Algorithmus bezeichnet wird. Und wir diskutieren im Allgemeinen die Zeitkomplexität im schlimmsten Fall.

Empfohlene Kurse: C-Sprach-Tutorial

Raumkomplexität:

Die Raumkomplexität des Algorithmus ist kein tatsächlich belegter Raum , sondern um die Anzahl der Hilfsraumeinheiten im gesamten Algorithmusraum zu berechnen, was nichts mit der Größe des Problems zu tun hat. Die Raumkomplexität S(n) eines Algorithmus ist definiert als die Größenordnung des vom Algorithmus verbrauchten Raums.

S(n)=o(f(n))

Wenn der für die Algorithmusausführung erforderliche Hilfsraum eine Konstante relativ zu den Eingabedaten n ist, wird er als Raumkomplexität bezeichnet Algorithmus Der Hilfsraum ist o(1);

Die Raumkomplexität des rekursiven Algorithmus: die Rekursionstiefe n*der für jede Rekursion erforderliche Hilfsraum ist eine Konstante Die Komplexität des rekursiven Raums ist o (n).

Die Berechnungsgleichung der Zeitkomplexität des rekursiven Algorithmus ist eine rekursive Gleichung:

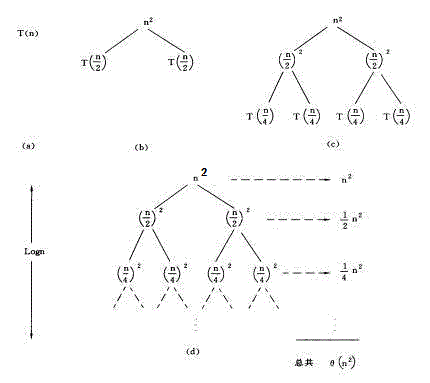
Ein Beispiel kann vor der Einführung berücksichtigt werden der rekursive Baum:

T(n) = 2T(n/2) + n2

2 Mal iterieren, um zu erhalten:

T(n) = n2 + 2(2T(n/4) + (n/2) 2)

Sie können ihn auch weiter iterieren und vollständig erweitern, um zu erhalten:

T(n) = n2 + 2((n/2) 2 +
2((n/22)2 + 2((n/23) 2 +
2((n/24) 2 +…+2((n/2i) 2 +
2T(n/2i + 1)))…))))……(1)

Und wenn n/2i+ 1 == 1 , die Iteration endet.

Erweitern Sie die Klammern von Gleichung (1), wir erhalten:

T(n) = n2 + 2(n/2)2 +
22(n/22) 2 + … + 2i(n/2i)2 +
2i+1T(n/2i+1)

Dies ist zufällig eine Baumstruktur, aus der die rekursive Baummethode abgeleitet werden kann.

(a)(b)(c)(d) in der Abbildung sind die Schritte 1, 2, 3 bzw. n in der rekursiven Baumgenerierung. In jedem Knoten wird das aktuelle freie Element n2 beibehalten und die beiden rekursiven Elemente T(n/2)
+ T(n/2) werden jeweils seinen beiden untergeordneten Knoten zugewiesen, und so weiter.

Die Summe aller Knoten im Diagramm ist:

[1 + 1/2 + (1/2)2 + (1/2)3 + … + (1/2)i] n2 = 2n2

Es ist ersichtlich, dass seine zeitliche Komplexität O(n2)

Die Regel ist des rekursiven Baums kann erhalten werden als:

(1) Der Knoten jeder Schicht ist der Wert von f(n) in T(n) = kT(n / m) + f(n) am aktuell n/m;

(2) Die Anzahl der Zweige jedes Knotens beträgt k;

(3) Die rechte Seite jeder Ebene markiert die Summe aller Knoten in der aktuellen Ebene.

Ein weiteres Beispiel:

T(n) = T(n/3) + T(2n/3) + n

Es ist rekursiv Der Baum ist wie folgt:

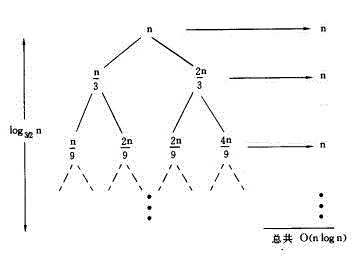
Es ist ersichtlich, dass der Wert jeder Schicht n ist und der längste Pfad von der Wurzel zum Blattknoten ist:

Denn am Ende stoppt die Rekursion bei (2/3)kn == 1. Dann

dann

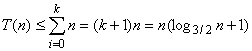
, das heißt , T(n) = O(nlogn)　

Zusammenfassend verwenden Sie diese Methode, um die Komplexität des rekursiven Algorithmus zu lösen:

f(n) = af(n/b) + d(n)

1 d(n) ist eine Konstante:

　

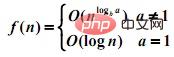
2 Wenn d(n) = cn:

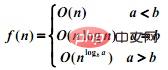
3. Der Rekursionsbaum kann verwendet werden, wenn d(n) in anderen Fällen eine Analyse durchführt.

Wenn im zweiten Fall die Divide-and-Conquer-Methode zur Verbesserung des ursprünglichen Algorithmus verwendet wird, liegt der Schwerpunkt auf der Verwendung neuer Berechnungsmethoden, um den Wert von a zu reduzieren. ​

Das obige ist der detaillierte Inhalt vonWie hoch ist die zeitliche Komplexität eines rekursiven Algorithmus?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!