Java implementiert eine zirkuläre Warteschlange
Dec 31, 2019 pm 05:14 PM
Vorteile von zirkulären Warteschlangen
Gewöhnliche Warteschlangeneinreihungsvorgänge sind teuer: Bei Entnahmevorgängen müssen alle Elemente nach Index 0 verschoben werden Je mehr Elemente vorhanden sind, desto mehr Zeit wird verbraucht und die Zeitkomplexität beträgt O(N).
Die Logik der kreisförmigen Warteschlange:
1. Wenn nur wenige Elemente vorhanden sind (die Endposition befindet sich hinter der Vorderseite), hat die kreisförmige Warteschlange den gleichen Warteschlangenvorgang Als normale Warteschlange werden die Elemente der Warteschlange an der Endposition platziert und dann wird die Tail++-Operation ausgeführt. Wenn das Element aus der Warteschlange entfernt wird, wird die vordere Position auf Null gesetzt und dann wird die Front++-Operation ausgeführt ; Zu diesem Zeitpunkt kann die Heckposition noch wie folgt hinter der Vorderseite beibehalten werden. Wie im Bild gezeigt:
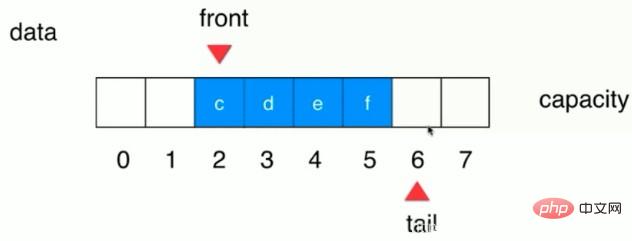
2. Während weiterhin Elemente hinzugefügt werden, das letzte Das Element wird an Index 7 platziert. Zu diesem Zeitpunkt wird die Endposition zum Index vor dem Kopf der Warteschlange verschoben. An der Position 0 beträgt der Endindex im Array: (Ende + 1) % Kapazität wie in der folgenden Abbildung gezeigt:
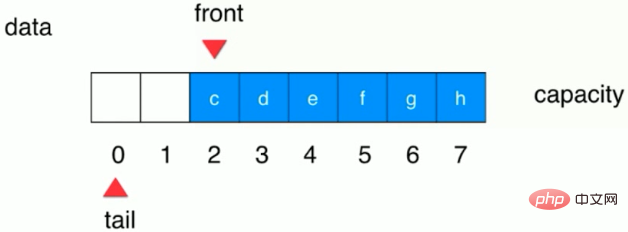
3. Wenn weiterhin Elemente hinzugefügt werden, wird das Element an der Schwanzposition hinzugefügt und der Schwanz bewegt sich weiter rückwärts. wie in der folgenden Abbildung gezeigt:

4. Fügen Sie weitere Elemente hinzu, wenn der Schwanz und die Vorderseite noch eine Einheit voneinander entfernt sind. Zu diesem Zeitpunkt ist also noch ein Freier Speicherplatz im Array, aber das aktuelle Array kann den Einfügevorgang der zirkulären Warteschlange nicht mehr implementieren, da die Bedingung für die zirkuläre Warteschlange, um zu beurteilen, dass die Warteschlange leer ist, front == tail ist, sodass hier eine Erweiterungsoperation erforderlich ist Zeit; Hier wird also bewusst Platz verschwendet.
Hier lässt sich ableiten, dass die Bedingung dafür, dass das kreisförmige Warteschlangenelement voll ist, lautet: Schwanz +1 == vorne (vorläufige Schlussfolgerung: Es wird auf (Schwanz + 1) % Kapazität == vorne verbessert)
5. Wenn der Vorgang zum Entfernen aus der Warteschlange fortgesetzt wird, springt die Position von vorne auch vom rechten Ende des Arrays zum linken Ende des Arrays. Zu diesem Zeitpunkt lautet der Frontindex im Array: (Front + 1) % Kapazität
Code-Implementierung: (Verwandte Video-Tutorial-Freigabe: Java-Video-Tutorial )
package dataStructure.chapter3;
/**
* @Author: zjtMeng
* @Date: 2019/12/28 20:13
* @Version 1.0
*/
public class LoopQueue<E> implements Queue<E> {
private E[] data;
private int front,tail;
private int size;
public LoopQueue(int capacity){
data = (E[]) new Object[capacity+1];
}
public LoopQueue(){
this(10);
}
public int getCapacity(){
return data.length-1;
}
/**
* 循环队列入队操作
* @param e
*/
@Override
public void enqueue(E e) {
//循环队列元素满的判断条件,如果满了就进行扩容操作,扩大两倍
if ((tail+1)%data.length == front)
resize(2 * getCapacity());
data[tail] = e;
tail = (tail + 1) % data.length;
size ++;
}
/**
* 循环队列扩容
* @param newCapacity
*/
private void resize(int newCapacity){
E[] newData = (E[]) new Object[newCapacity+1];
//循环队列第一种遍历方式
for (int i = 0 ; i < size ; i++ ){
//newData[]中的元素与data[]中的元素,一方面存在着front的偏移量,另一方面,data[]中的元素,
//可能在有部分处于front前面,因此此处采用对数组长度取余,来判断元素的位置
newData[i] = data[(i+front)%data.length];
}
data = newData;
front =0;
tail = size;
}
@Override
public E dequeue() {
//首先判断队列是否为空,如果为空则抛出异常
if (isEmpty())
throw new IllegalArgumentException("Cannot dequeue from an empty queue.");
E ret = data[front];
//引用地址需要置空,否则JVM不能及时回收空间,从而可能会出现OOM异常
data[front] = null;
front = (front + 1 )% data.length;
size--;
//如果元素数量达到队列容积的1/4,且队列容积/2 不等于0时,进行缩容操作
if (size == getCapacity() / 4 && getCapacity() / 2 != 0 )
resize(getCapacity() / 2);
return ret;
}
/**
* 查看队首元素
* @return
*/
@Override
public E getFront() {
if (isEmpty())
throw new IllegalArgumentException("Queue is empty.");
return data[front];
}
@Override
public int getSize() {
return size;
}
/**
* 判断循队列是否为空
* @return
*/
@Override
public boolean isEmpty() {
return front == tail;
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
res.append(String.format("Queue: size = %d, capacity = %d\n",size, getCapacity()));
res.append("front[");
//循环队列遍历的第二种方法
for (int i = front; i != tail; i = (i + 1) % data.length){
res.append(data[i]);
//循环队列未遍历到队尾的标志
if ((i + 1) % data.length != tail)
res.append(", ");
}
res.append("] tail");
return res.toString();
}
}Empfohlene verwandte Artikel und Tutorials: Java-Einführungs-Tutorial
Das obige ist der detaillierte Inhalt vonJava implementiert eine zirkuläre Warteschlange. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heißer Artikel

Hot-Tools-Tags

Heißer Artikel

Heiße Artikel -Tags

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Brechen oder aus Java 8 Stream foreach zurückkehren?
Feb 07, 2025 pm 12:09 PM
Brechen oder aus Java 8 Stream foreach zurückkehren?














