Verstehen Sie das B + Tree-Indexprinzip von MySQL genau
Zuallererst ist die korrekte Erstellung geeigneter Indizes die Grundlage für die Verbesserung der Datenbankabfrageleistung.
Was ist ein Index?
Ein Index ist eine dezentrale Speicherdatenstruktur, die erstellt wurde, um das Abrufen von Datenzeilen in einer Tabelle zu beschleunigen.
Wie funktioniert der Index?
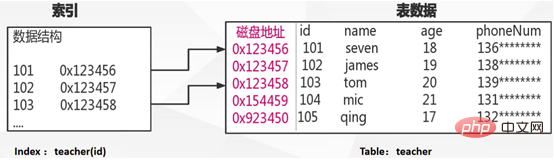
Wie im Bild oben gezeigt, wählen Sie * von Lehrer aus, wenn es eine SQL-Anweisung gibt, wobei die ID = 101 ist, wenn keine vorhanden ist index, Um diesen Datensatz zu finden, müssen wir die gesamte Tabelle scannen und die Daten mit der ID = 101 abgleichen. Wenn wir einen Index haben, können wir über den Index schnell die Adresse der Zeile finden, die 101 auf der Festplatte entspricht, und dann die entsprechenden Zeilendaten basierend auf der angegebenen Adresse abrufen.
Warum verwendet die MYSQL-Datenbank B+TREE als Indexdatenstruktur?
Um das Abrufen von Daten zu beschleunigen, fällt mir als Erstes der Binärbaum ein. Die Suchzeitkomplexität des Binärbaums kann O(log2(n)) erreichen. Werfen wir einen Blick auf die Speicherstruktur des Binärbaums:
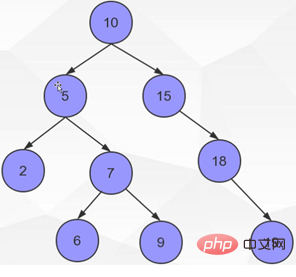
Binärbaumsuche entspricht einer binären Suche. Die binäre Suche kann die Effizienz von Abfragen erheblich verbessern, weist jedoch ein Problem auf: Der Binärbaum verwendet die ersten eingefügten Daten als Wurzelknoten. Wenn Sie nur auf die rechte Seite schauen, werden Sie feststellen, dass dies der Fall ist ist eine lineare verknüpfte Listenstruktur. Wenn unsere aktuellen Daten nur 1, 2, 3, 4, 5, 6 enthalten, tritt die folgende Situation ein:
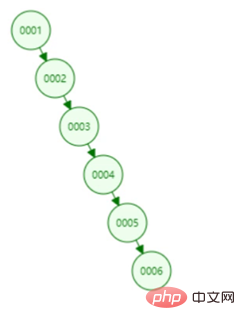
Wenn die Daten, die wir abfragen möchten, 6 sind, werden wir Nur durch Durchlaufen aller Knoten können wir 6 finden, was einem vollständigen Tabellenscan entspricht. Aufgrund dieses Problems ist der binäre Suchbaum nicht für die Verwendung als Indexdatenstruktur geeignet.
Auf der Grundlage einer solchen Schlussfolgerung ist es leicht, sich einen ausgeglichenen binären Suchbaum vorzustellen, um das Problem der linearen verknüpften Liste zu lösen. Schauen wir uns an, wie ein ausgeglichener Binärbaum aussieht:
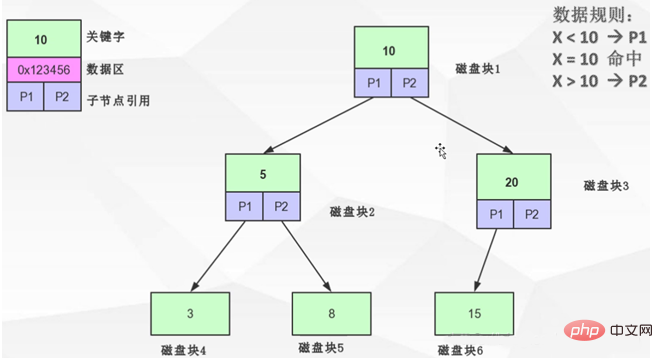
Ein ausgeglichener binärer Suchbaum ist definiert als: Der Höhenunterschied zwischen den untergeordneten Knoten eines Knotens darf 1 nicht überschreiten Wie in Knoten 20 in der Abbildung oben gezeigt, beträgt die Knotenhöhe links 1, die Knotenhöhe rechts 0 und die Differenz 1, sodass das obige Bild nicht gegen die Definition verstößt. Es handelt sich um einen ausgeglichenen Binärbaum. Die Möglichkeiten, das Gleichgewicht eines Binärbaums sicherzustellen, sind Links- und Rechtsoperationen sowie andere Operationen. Sie können selbst nach relevantem Wissen suchen.
Wenn der ausgeglichene Binärbaum im obigen Bild den ID-Index speichert, beginnen Sie nun mit den Daten von id = 8, laden Sie zuerst den Wurzelknoten in den Speicher, vergleichen Sie 8 und 10 und stellen Sie fest, dass 8 ist kleiner als 10, fahren Sie fort. Laden Sie den linken Teilbaum von 10. Laden Sie 5 in den Speicher und vergleichen Sie 8 mit 5. Laden Sie auf die gleiche Weise den rechten Teilbaum von Knoten 5. Zu diesem Zeitpunkt wurde ein Treffer gefunden und nun werden die Daten geladen, die dem Index mit der ID 8 entsprechen.
Wie finde ich die dem Index entsprechenden Daten?
Es gibt im Allgemeinen zwei Möglichkeiten, Daten in einem Index zu speichern. Die erste besteht darin, den gesamten spezifischen Dateninhalt der Zeilendaten mit der ID = 8 im Datenbereich des Knotens zu speichern. Auf andere Weise speichert der Datenbereich die Festplattenadresse, auf der die Daten tatsächlich gespeichert sind.
An diesem Punkt löst der ausgeglichene Binärbaum das Problem linearer verknüpfter Listen. Die Effizienz der Datenabfrage scheint im Grunde in Ordnung zu sein und erreicht O(log2(n)). eine Datenstruktur? Welche Probleme hat er?
Problem 1: Unzureichende Sucheffizienz Im Allgemeinen bestimmt die Tiefe der Daten die Anzahl der IOs während der Suche. Wie in der Abbildung oben gezeigt, sind für die Suche nach Daten mit der ID = 8 3 E/A erforderlich. Wenn die Datenmenge Millionen erreicht, wird die Höhe des Baums erschreckend sein.
Problem 2: Die Abfrage ist nicht stabil. Wenn die abgefragten Daten auf den Stammknoten fallen, ist nur ein IO erforderlich. Wenn es sich um einen Blattknoten oder einen Zweigknoten handelt, sind mehrere IOs erforderlich.
Problem 3: Der Knoten speichert zu wenig Dateninhalt. Es nutzt weder die Betriebssystem- und Festplattendatenaustauschfunktionen noch die Read-Ahead-Fähigkeit von Festplatten-E/A sinnvoll aus. Da ein Datenaustausch zwischen dem Betriebssystem und der Festplatte in Seiteneinheiten erfolgt, eine Seite = 4 KB, lädt das Betriebssystem für jeden IO 4 KB Daten in den Speicher. Die Struktur jedes Knotens im Binärbaum speichert jedoch nur ein Schlüsselwort, einen Datenbereich und zwei untergeordnete Knotenreferenzen, die nicht 4 KB Inhalt füllen können. Glücklicherweise habe ich einmal eine E/A-Operation durchgeführt, aber nur ein Schlüsselwort wurde geladen. Wenn die Höhe des Baums sehr hoch ist und sich das gesuchte Schlüsselwort zufällig an einem Blattknoten oder einem Zweigknoten befindet, dauert es viele Male, bis ein Schlüsselwort abgerufen wird Stichwort. IO.
Gibt es eine Struktur, die dieses Problem der Binärbäume lösen kann?
Ja, mehrweg ausgeglichener Suchbaum: (Balance Tree):
B Tree ist ein absolut ausgeglichener Baum, alle Blattknoten sind auf der gleichen Höhe, wie im gezeigt folgende Abbildung:
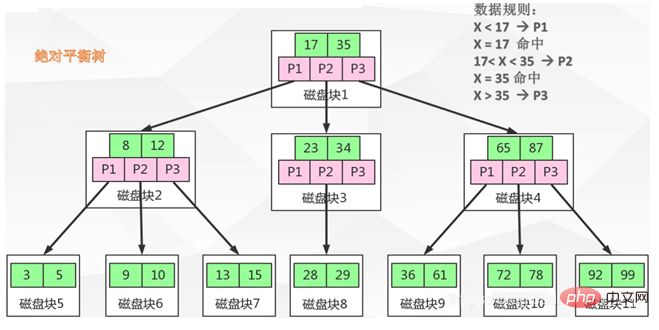
Was sind die Vorteile von B Tree und wie löst es einige Probleme?
Sehen wir uns zunächst die Definition an. Das Bild oben zeigt einen 2-3-Baum (jeder Knoten speichert 2 Schlüsselwörter und hat 3 Wege). Wie aus der Abbildung ersichtlich ist, ist die Beziehung zwischen der Anzahl der in jedem Knoten gespeicherten Schlüsselwörter und der Anzahl der Pfade:
Anzahl der Schlüsselwörter = Anzahl der Pfade – 1.
Angenommen, Sie möchten die Daten mit der ID = 28 aus dem obigen Bild finden. Der B TREE-Suchvorgang ist wie folgt:
Laden Sie zuerst den Wurzelknoten in den Speicher und laden Sie die beiden Schlüsselwörter 17 und 35. Die Beurteilungsregel lautet:

Nachdem Sie gemäß den obigen Regeln 28 erreicht haben, laden Sie die Daten, die 28 entsprechen, und suchen Sie dann den entsprechenden Datenbereich 28. Der Datenbereich speichert die spezifischen Daten oder einen Zeiger auf die Daten.
Warum kann diese Struktur das Problem ausgeglichener Binärbäume lösen?
kann die interaktiven Eigenschaften des Betriebssystems und der Festplatte gut nutzen. Um die Lesefähigkeit der Festplatte optimal zu nutzen, setzt MYSQL die Seitengröße auf 16 KB ist die Größe eines Knotens (Festplattenblocks) 16 KB, ein IO lädt den Inhalt eines Knotens (16 KB) in den Speicher. Nehmen Sie hier an, dass der Schlüsselworttyp int ist, was 4 Bytes entspricht. Wenn der Datenbereich, der jedem Schlüsselwort entspricht, ebenfalls 4 Bytes beträgt, kann jeder Knoten in der obigen Abbildung ungefähr ( 16 * 1000) speichern. / 8 = 2000 Schlüsselwörter, dann gibt es insgesamt 2001 Möglichkeiten. Für einen Binärbaum mit drei Höhenebenen können bis zu 7 Schlüsselwörter gespeichert werden. Bei diesem B-Baum mit 2001 Pfaden ist die Anzahl der Schlüsselwörter, nach denen mit drei Höhenebenen gesucht werden kann, jedoch weitaus größer als bei a Binärbaum.
Während B TREE das Gleichgewicht des Baums sicherstellt, führt jede Änderung der Schlüsselwörter zu großen Änderungen in der Struktur. Dieser Prozess ist besonders zeitaufwändig. Daher müssen Sie beim Erstellen eines Index einen erstellen Geeigneter Index: Anstatt Indizes für alle Felder zu erstellen, erhöht die Erstellung redundanter Indizes nur den Leistungsverbrauch beim Hinzufügen, Löschen und Ändern von Daten.
Da B-Tree das Problem sehr gut gelöst hat, warum verwendet MYSQL immer noch B+TREE?
Sehen wir uns zunächst an, wie B+TREE eine Variante von B+-Baumarten ist, die Beziehung zwischen der Anzahl der Pfade in B-Baumarten Schlüsselwörter gelten nicht mehr. In B+TREE verwendet die Datenabrufregel ein links geschlossenes Intervall und die Beziehung zwischen der Anzahl der Pfade und der Anzahl der Schlüssel beträgt 1:1, wie in der folgenden Abbildung dargestellt:
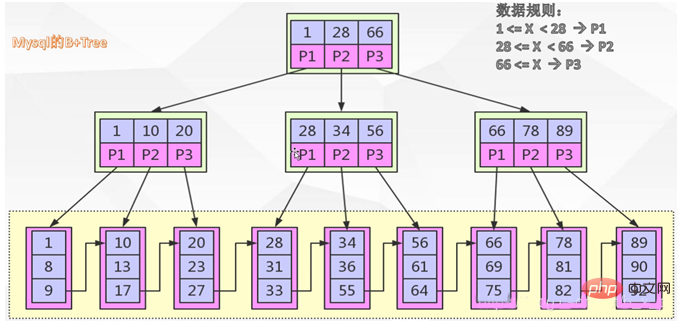
Wenn das obige Bild ein Index ist, der nach ID = 1 erstellt wurde, lauten die Suchregeln wie folgt:

Gemäß den oben genannten Regeln werden die Daten schließlich im Blattknoten erfasst. Erhalten Sie die tatsächlichen Daten entsprechend dem Datenbereich von Knoten 1 im Blattknoten.
Was ist der Unterschied zwischen B TREE und B+TREE?
1. Die B+TREE-Schlüsselwortsuche verwendet das linke geschlossene Intervall, weil es die automatische Inkrementierung von IDs am besten unterstützen soll Absicht von MySQL. Das heißt, wenn id = 1 trifft, wird die Suche fortgesetzt, bis 1 im Blattknoten gefunden wird.
2. Der B+TREE-Wurzelknoten und der Zweigknoten haben keinen Datenbereich und die dem Schlüsselwort entsprechenden Daten werden nur im Blattknoten gespeichert. Das heißt, nur der Schlüsselwortdatenbereich im Blattknoten speichert den tatsächlichen Dateninhalt oder die Adresse des Inhalts. Wenn in der B-Baumart der Wurzelknoten getroffen wird, werden die Daten direkt zurückgegeben. Und in B+TREE speichern Blattknoten keine Verweise auf untergeordnete Knoten.
3. B+TREE-Blattknoten sind sequentiell angeordnet und benachbarte Knoten haben eine sequentielle Referenzbeziehung. Wie in der Abbildung oben gezeigt, sind die Blattknoten durch Zeiger verbunden.
Warum hat sich MYSQL am Ende für B+TREE entschieden?
1. B+TREE ist eine Variante von B TREE. Die Probleme, die B TREE lösen kann, können auch von B+TREE gelöst werden (die Höhe des Baums verringern und die darin gespeicherte Datenmenge erhöhen). Knoten)
2. B+TREE verfügt über stärkere Datenbank- und Tabellenscanfunktionen. Wenn wir die Datentabelle basierend auf dem Index scannen möchten, müssen wir den gesamten Baum durchlaufen, während B+ TREE muss nur alle Blattknoten durchlaufen (es gibt Referenzen zwischen Blattknoten).
3. B+TREE verfügt über stärkere Lese- und Schreibfunktionen auf der Festplatte. Wenn alle Stammknoten und Unterstützungsknoten die gleiche Größe haben, sind die gespeicherten Schlüsselwörter größer die von B TREE. Willst du mehr. Blattknoten speichern keine Referenzen auf untergeordnete Knoten. Daher liest und schreibt B+TREE mehr auf die Festplatte geladene Schlüsselwörter als B TREE.
4. B+TREE verfügt über eine stärkere Sortierfunktion. Wie aus dem Bild oben ersichtlich ist, verfügt B+TREE natürlich über eine Sortierfunktion.
5. Die Effizienz der B+TREE-Abfragen ist stabiler. Bei jeder Datenabfrage muss die Anzahl der E/A-Abfragen stabil sein. Natürlich hat jeder ein anderes Verständnis davon, denn wenn in B TREE der Wurzelknoten trifft, kehrt er direkt zurück, was in der Tat effizienter ist.
Die spezifische Implementierungsform von MYSQL B+TREE
Die Haupterklärung hier ist die Implementierung der beiden Speicher-Engines von MYSQL (MYISAM und INNODB) basierend auf unterschiedlichen B+TREE-Indexstrukturen. Suchen Sie zunächst den Ordner, in dem MYSQL Daten speichert, und sehen Sie, wie MySQL Daten speichert:

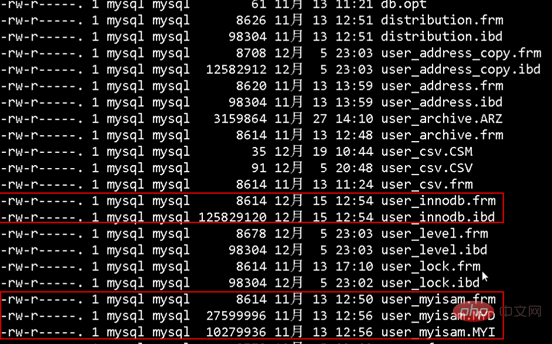
Geben Sie dieses Verzeichnis ein, in dem alle Datenbanken gespeichert sind, und geben Sie dann ein bestimmtes Datenbankverzeichnis ein. Hier gibt es verschiedene Datenspeicher-Engines. Hier erklären wir MYISAM und innodb, wie in der Abbildung gezeigt:
MYISAM-Speicher-Engine-Index:
Wie in der Abbildung zu sehen ist, gibt es drei Dateien, die die MYISAM-Speicher-Engine zum Speichern von Datenbankdaten verwenden:
Frm, die Tabellendefinitionsdatei. MYD: Datendatei, alle Daten werden in dieser Datei gespeichert. MYI: Indexdatei.
In der MYISAM-Speicher-Engine ist die Beziehung zwischen Daten und Index wie folgt:
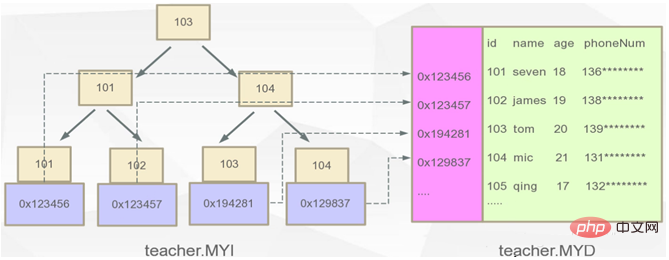
Wie finde ich Daten? Wenn Sie die Daten mit der ID = 101 abfragen möchten, suchen Sie zunächst den Knoten mit der ID = 101 gemäß der MYI-Indexdatei (wie in der Abbildung oben links gezeigt) und ermitteln Sie über die Daten die Festplattenadresse, unter der die Daten tatsächlich gespeichert sind Bereich dieses Knotens und verwenden Sie dann diese Adresse, um die Daten aus der MYD-Datendatei abzurufen (Wie rechts in der Abbildung oben gezeigt) Laden Sie den entsprechenden Datensatz.
Wenn mehrere Indizes vorhanden sind, lautet der Ausdruck wie folgt:
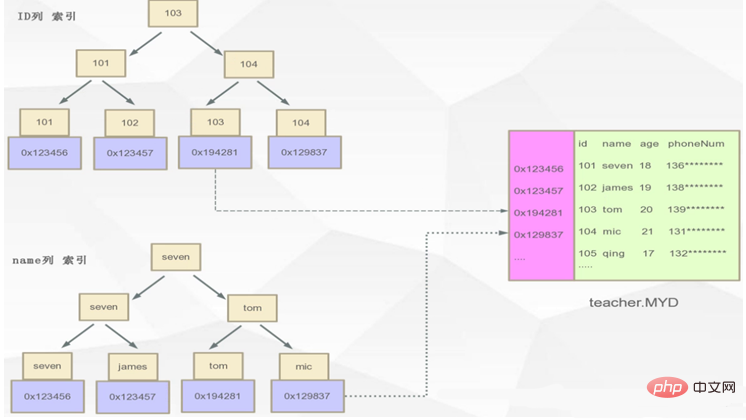
In der MYISAM-Speicher-Engine befinden sich also der Primärschlüsselindex und der Hilfsindex bei die gleiche Ebene, und es gibt keinen Primärschlüsselindex.
Innodb-Speicher-Engine:
Schauen wir uns zunächst das Konzept eines Clustered-Index an. Ein Clustered-Index ist definiert als: Die physische Reihenfolge der Daten in den Datenbanktabellenzeilen entspricht der logischen Reihenfolge der Schlüsselwerte.
Innodb verwendet Primärschlüssel als Indizes, um die Datenspeicherung zu aggregieren und zu organisieren. Schauen wir uns an, wie Innodb Daten organisiert.
Innodb verfügt nur über zwei Dateien, die FRM-Datei: die Tabellendefinitionsdatei und die Ibd-Datei. Es gibt keine Datei speziell zum Speichern von Daten. Daten werden mithilfe von Primärschlüsseln aggregiert und gespeichert, und die tatsächlichen Daten werden in Blattknoten gespeichert. Die ursprüngliche Entwurfsabsicht von innodb besteht darin, dass der Primärschlüssel der wichtigste Index ist. Genauer gesagt, wie in der folgenden Abbildung gezeigt:
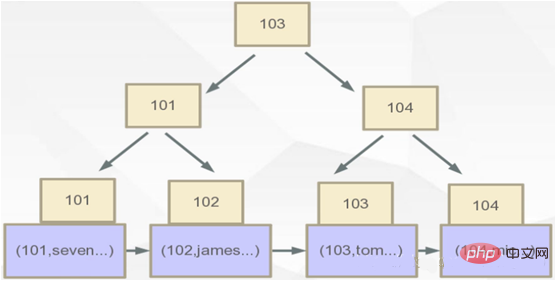
Wie in der obigen Abbildung gezeigt, speichert der Datenbereich des Blattknotens beim Abrufen über den Index die tatsächlichen Daten. Durch Klicken auf den Blattknoten können Zeilendaten direkt vom Blattknoten abgerufen werden. Vor der MySQL5.5-Version wurde die MYISAM-Engine verwendet, und nach 5.5 wurde die Innodb-Engine verwendet.
In innodb ist das Format des Hilfsindex wie in der folgenden Abbildung dargestellt?
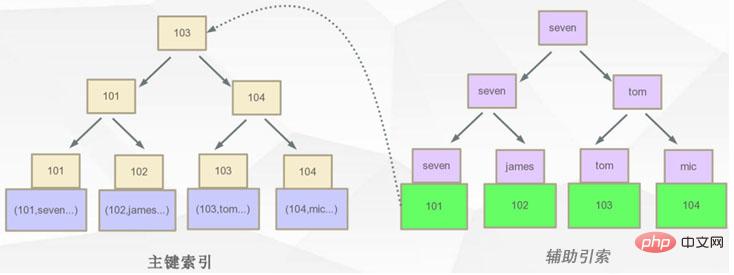
Wie oben gezeigt, speichern die Blattknoten des Primärschlüsselindex die realen Daten. Der Datenbereich des Hilfsindexblattknotens speichert den Wert des Primärschlüsselindexschlüssels. Der Suchvorgang ist: Wenn Sie die Daten mit dem Namen = sieben abfragen möchten, fragen Sie zuerst den Hilfsindex ab und finden Sie schließlich die Primärschlüssel-ID = 101. Suchen Sie dann im Primärschlüsselindex nach den Daten mit der ID 101 und erhalten Sie sie schließlich die realen Daten aus dem Blattknoten des Primärschlüsselindex. Daher erfordert das Abrufen über den Hilfsindex ein zweimaliges Abrufen des Index.
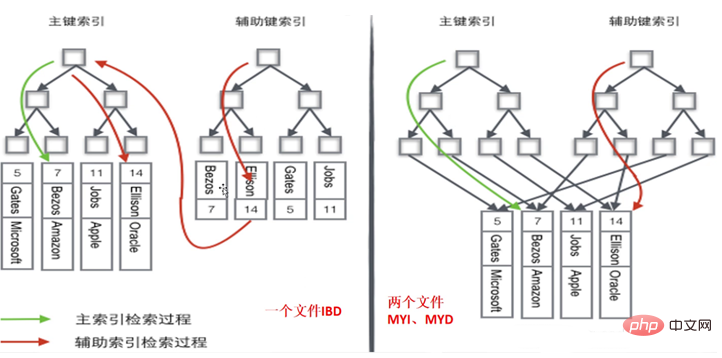
Stellen Sie den Unterschied zwischen Innodb und MYISAM in einem Bild dar, wie unten gezeigt:
Mehrere Prinzipien für die Erstellung von Indizes:
1. Der diskrete Typ der Spalte:
Die Berechnungsformel des diskreten Typs: count(distinct col):count(col) Je höher der diskrete Typ, desto besser der Auswahltyp.
Welche Spalte hat für jedes Feld in der folgenden Tabelle den besten diskreten Typ:
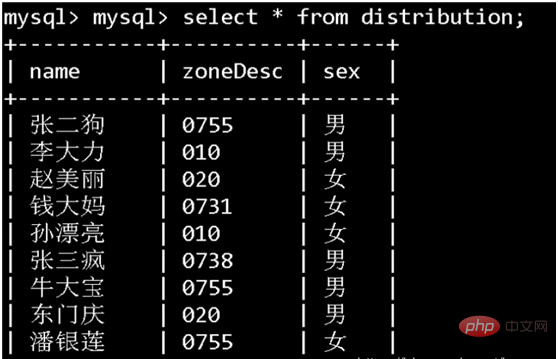
Aus dem obigen Bild ist deutlich zu erkennen, dass der diskrete Typ Der Namenstyp ist der beste, wenn Sie Sex verwenden, um einen Index zu erstellen:
Warum heißt es, dass der selektive Typ umso besser ist, je höher der diskrete Typ ist?
Wie unten gezeigt, sieht die Indexstruktur wie folgt aus, wenn Sie einen Index für Sex erstellen:
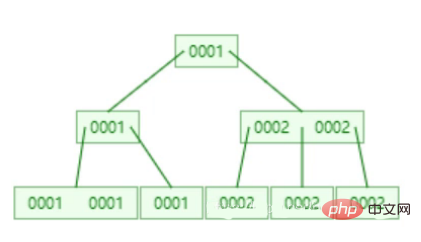
Wenn Sie die Daten von abrufen Zu diesem Zeitpunkt ist Geschlecht = 1. Wenn der Wurzelknoten beurteilt wird, besteht das Ergebnis darin, den linken Teilbaum abzufragen. Wenn jedoch die Beurteilung auf der zweiten Ebene des linken Teilbaums erfolgt, erfüllen sowohl der linke als auch der rechte Zweig die Bedingungen Es ist schwierig zu entscheiden, welchen Zweig man wählen soll, um die Suche fortzusetzen, oder die beiden Zweige gleichzeitig zu durchsuchen.
2. Prinzip der Übereinstimmung ganz links
Beim Vergleich von Schlüsselwörtern im Index muss der Vergleich von links nach rechts erfolgen und kann nicht übersprungen werden. Die zuvor erläuterten IDs sind alle int-Daten. Wenn die ID eine Zeichenfolge ist, sieht sie wie folgt aus:
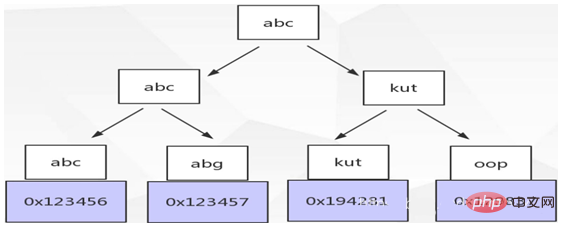
Beim Abgleich wird die Zeichenfolge in ASCLL-Code konvertiert, z. B. abc wird zu 97 98 99, und dann Zeichen für Zeichen von links nach rechts verglichen. Daher ist der Index bei Verwendung von %a in einer SQL-Abfrage ungültig, da % eine vollständige Übereinstimmung bedeutet. Es ist nicht erforderlich, die gesamte Tabelle direkt zu scannen.
3. Prinzip des kleinsten Speicherplatzes
Wie bereits erwähnt, ist die Anzahl der in jedem Knoten gespeicherten Schlüsselwörter größer, die jeweils in den Speicher geladen werden, wenn der von Schlüsselwörtern belegte Platz kleiner ist Je mehr Schlüsselwörter vorhanden sind, desto höher ist die Sucheffizienz.
Gewerkschaftsindex:
Einzelspaltiger Index: Schlüsselwort [Name] im Knoten
Gemeinsamer Index: Schlüsselwort im Knoten [Name, Telefonnummer]
Einzel- Spaltenindizes können als spezielle gemeinsame Indizes betrachtet werden, und der Vergleich gemeinsamer Indizes basiert ebenfalls auf dem Prinzip der Übereinstimmung ganz links.
Grundsätze für die Auswahl gemeinsamer Indexspalten:
(1) Häufig verwendete Spaltenpriorität (Prinzip der Übereinstimmung ganz links)
(2) Spaltenpriorität mit hoher Diskretion (diskretes Prinzip von hoch). Grad)
(3) Spaltenpriorität mit geringer Breite, (Prinzip des geringsten Abstands)
Das Folgende ist ein einfaches Beispiel für Probleme, die im täglichen Leben häufig auftreten:
Zum Beispiel lautet die häufig verwendete SQL-Abfrage wie folgt:
Select * from users where name = ?
Select * from users where name = ? and pahoneNum = ?
Um den Abruf zu beschleunigen, erstellen Sie einen Index für Die obige SQL-Abfrage lautet wie folgt:
Create index idx_name on users(name)
Create index idx_name_phoneNum on users(name, phoneNum)
In der obigen Lösung ist idx_name gemäß dem am weitesten links stehenden Matching-Prinzip ein redundanter Index, wobei name = ? kann auch über den Index idx_name_phoneNum abgerufen werden. Redundante Indizes erhöhen oder verringern den Leistungsverbrauch bei der Aufrechterhaltung des B+TREE-Gleichgewichts und belegen Speicherplatz.
Abgedeckter Index:
Wenn die abgefragte Spalte direkt über die Informationen des Indexelements zurückgegeben werden kann, wird der Index als abdeckender Index für die Abfrage von SQL bezeichnet. Durch das Abdecken von Indizes kann die Abfrageeffizienz verbessert werden.
Im Folgenden wird der Deckungsindex anhand eines Beispiels erläutert.
Tabelle: Lehrer
Index: PK(id), key(name, phoneNum), unique(teacherNo)
Welche der folgenden SQLs verwenden abdeckende Indizes?
Select teacherNo from teacher where teacherNo = ?: Bei Verwendung kann beim Abrufen von teacherNo der Wert teacherNo im Index direkt zurückgegeben werden, ohne den Datenbereich einzugeben.
Select id,teacherNo from teacher where teacherNo = ?: Bei Verwendung speichert der Blattknoten des Hilfsindex den Wert des Primärindex, sodass beim Abrufen des Blattknotens des Hilfsindex die ID zurückgegeben werden kann.
Select name,phoneNum from teacher where teacherNo = ?: Nicht verwendet
Select phoneNum from teacher where name = ?, verwendet.
Nachdem Sie den Covering-Index kennen, werden Sie wissen, warum SQL erfordert, dass Sie versuchen, select * nicht zu verwenden und die spezifischen Felder anzugeben, die abgefragt werden sollen. Ein Grund dafür ist, dass Sie dies nicht tun müssen, wenn Sie den Covering-Index verwenden Geben Sie Sobald Sie sich im Datenbereich befinden, können die Daten direkt zurückgegeben werden, wodurch die Abfrageeffizienz verbessert wird.
Anhand der vorherigen Studie können wir die folgenden Schlussfolgerungen leicht verstehen:
1. Die Datenlänge der Indexspalte kann so klein wie möglich sein, wenn sie den Geschäftsanforderungen entspricht.
2. Je mehr Indizes in der Tabelle, desto besser.
3. In der Where-Bedingung, etwa 9 %, etwa %9 %, etwa %9, verwenden die drei Methoden den Index nicht. Die beiden letztgenannten Methoden sind für Indizes ungültig. Die ersten 9 % sind unsicher und hängen vom diskreten Typ der Spalte ab. Wenn sich die diskrete Situation als besonders schlecht herausstellt, ist der Abfrageoptimierer der Meinung, dass die Indexabfrageleistung schlechter ist, was jedoch nicht der Fall ist so gut wie ein vollständiger Tabellenscan.
4. Indizes können nicht für NOT IN in der Where-Bedingung verwendet werden
5. Verwenden Sie die angegebenen Abfragen häufiger, geben Sie nur die gewünschten Spalten zurück und verwenden Sie select * weniger.
6. Wenn die Funktion in der Abfragebedingung verwendet wird, ist der Index ungültig. Dies hängt mit dem diskreten Typ der Spalte zusammen. Sobald die Funktion verwendet wird, ist sie unsicher.
7. Wenn die Suche im gemeinsamen Index nicht in der Spalte ganz links gestartet wird, kann der Index nicht verwendet werden.
8. Um den gemeinsamen Index genau der Spalte ganz links zuzuordnen und ihn an eine andere Spalte anzupassen, kann der Index verwendet werden.
9. Wenn die Abfrage im gemeinsamen Index eine Bereichsabfrage einer bestimmten Spalte enthält, können nicht alle Spalten rechts davon den Index verwenden.
Empfohlenes MySQL-Tutorial „MySQL-Tutorial “
Das obige ist der detaillierte Inhalt vonVerstehen Sie das B + Tree-Indexprinzip von MySQL genau. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1655
1655
 14
14
 1414
1414
 52
52
 1307
1307
 25
25
 1253
1253
 29
29
 1228
1228
 24
24
 MySQLs Rolle: Datenbanken in Webanwendungen
Apr 17, 2025 am 12:23 AM
MySQLs Rolle: Datenbanken in Webanwendungen
Apr 17, 2025 am 12:23 AM
Die Hauptaufgabe von MySQL in Webanwendungen besteht darin, Daten zu speichern und zu verwalten. 1.Mysql verarbeitet effizient Benutzerinformationen, Produktkataloge, Transaktionsunterlagen und andere Daten. 2. Durch die SQL -Abfrage können Entwickler Informationen aus der Datenbank extrahieren, um dynamische Inhalte zu generieren. 3.Mysql arbeitet basierend auf dem Client-Server-Modell, um eine akzeptable Abfragegeschwindigkeit sicherzustellen.
 So starten Sie MySQL von Docker
Apr 15, 2025 pm 12:09 PM
So starten Sie MySQL von Docker
Apr 15, 2025 pm 12:09 PM
Der Prozess des Startens von MySQL in Docker besteht aus den folgenden Schritten: Ziehen Sie das MySQL -Image zum Erstellen und Starten des Containers an, setzen
 Beispiel für Laravel -Einführung
Apr 18, 2025 pm 12:45 PM
Beispiel für Laravel -Einführung
Apr 18, 2025 pm 12:45 PM
Laravel ist ein PHP -Framework zum einfachen Aufbau von Webanwendungen. Es bietet eine Reihe leistungsstarker Funktionen, darunter: Installation: Installieren Sie die Laravel CLI weltweit mit Komponisten und erstellen Sie Anwendungen im Projektverzeichnis. Routing: Definieren Sie die Beziehung zwischen der URL und dem Handler in Routen/Web.php. Ansicht: Erstellen Sie eine Ansicht in Ressourcen/Ansichten, um die Benutzeroberfläche der Anwendung zu rendern. Datenbankintegration: Bietet eine Out-of-the-Box-Integration in Datenbanken wie MySQL und verwendet Migration, um Tabellen zu erstellen und zu ändern. Modell und Controller: Das Modell repräsentiert die Datenbankentität und die Controller -Prozesse HTTP -Anforderungen.
 Lösen Sie das Datenbankverbindungsproblem: Ein praktischer Fall der Verwendung von Minii/DB -Bibliothek
Apr 18, 2025 am 07:09 AM
Lösen Sie das Datenbankverbindungsproblem: Ein praktischer Fall der Verwendung von Minii/DB -Bibliothek
Apr 18, 2025 am 07:09 AM
Bei der Entwicklung einer kleinen Anwendung stieß ich auf ein kniffliges Problem: die Notwendigkeit, eine leichte Datenbankbetriebsbibliothek schnell zu integrieren. Nachdem ich mehrere Bibliotheken ausprobiert hatte, stellte ich fest, dass sie entweder zu viel Funktionalität haben oder nicht sehr kompatibel sind. Schließlich fand ich Minii/DB, eine vereinfachte Version basierend auf YII2, die mein Problem perfekt löste.
 Laravel Framework Installationsmethode
Apr 18, 2025 pm 12:54 PM
Laravel Framework Installationsmethode
Apr 18, 2025 pm 12:54 PM
Artikelzusammenfassung: Dieser Artikel enthält detaillierte Schritt-für-Schritt-Anweisungen, um die Leser zu leiten, wie das Laravel-Framework einfach installiert werden kann. Laravel ist ein leistungsstarkes PHP -Framework, das den Entwicklungsprozess von Webanwendungen beschleunigt. Dieses Tutorial deckt den Installationsprozess von den Systemanforderungen bis zur Konfiguration von Datenbanken und das Einrichten von Routing ab. Durch die Ausführung dieser Schritte können die Leser schnell und effizient eine solide Grundlage für ihr Laravel -Projekt legen.
 MySQL und PhpMyAdmin: Kernfunktionen und Funktionen
Apr 22, 2025 am 12:12 AM
MySQL und PhpMyAdmin: Kernfunktionen und Funktionen
Apr 22, 2025 am 12:12 AM
MySQL und PhpMyAdmin sind leistungsstarke Datenbankverwaltungs -Tools. 1) MySQL wird verwendet, um Datenbanken und Tabellen zu erstellen und DML- und SQL -Abfragen auszuführen. 2) PHPMYADMIN bietet eine intuitive Schnittstelle für Datenbankverwaltung, Tabellenstrukturverwaltung, Datenoperationen und Benutzerberechtigungsverwaltung.
 MySQL gegen andere Programmiersprachen: Ein Vergleich
Apr 19, 2025 am 12:22 AM
MySQL gegen andere Programmiersprachen: Ein Vergleich
Apr 19, 2025 am 12:22 AM
Im Vergleich zu anderen Programmiersprachen wird MySQL hauptsächlich zum Speichern und Verwalten von Daten verwendet, während andere Sprachen wie Python, Java und C für die logische Verarbeitung und Anwendungsentwicklung verwendet werden. MySQL ist bekannt für seine hohe Leistung, Skalierbarkeit und plattformübergreifende Unterstützung, die für Datenverwaltungsanforderungen geeignet sind, während andere Sprachen in ihren jeweiligen Bereichen wie Datenanalysen, Unternehmensanwendungen und Systemprogramme Vorteile haben.
 MySQL gegen andere Datenbanken: Vergleich der Optionen
Apr 15, 2025 am 12:08 AM
MySQL gegen andere Datenbanken: Vergleich der Optionen
Apr 15, 2025 am 12:08 AM
MySQL eignet sich für Webanwendungen und Content -Management -Systeme und ist beliebt für Open Source, hohe Leistung und Benutzerfreundlichkeit. 1) Im Vergleich zu Postgresql führt MySQL in einfachen Abfragen und hohen gleichzeitigen Lesevorgängen besser ab. 2) Im Vergleich zu Oracle ist MySQL aufgrund seiner Open Source und niedrigen Kosten bei kleinen und mittleren Unternehmen beliebter. 3) Im Vergleich zu Microsoft SQL Server eignet sich MySQL besser für plattformübergreifende Anwendungen. 4) Im Gegensatz zu MongoDB eignet sich MySQL besser für strukturierte Daten und Transaktionsverarbeitung.




