Was ist Rekursion?

Was ist Rekursion?

Die Programmiertechnik, bei der sich ein Programm selbst aufruft, wird Rekursion genannt.

Rekursion als Algorithmus wird häufig in Programmiersprachen verwendet. Ein Prozess oder eine Funktion verfügt über eine Methode, sich selbst direkt oder indirekt in ihrer Definition oder Beschreibung aufzurufen. Sie wandelt normalerweise ein großes und komplexes Problem in ein kleineres Problem um, das dem ursprünglichen Problem ähnelt, das nur mit einer kleinen Anzahl von Programmen gelöst werden kann um die mehrfach wiederholten Berechnungen zu beschreiben, die im Problemlösungsprozess erforderlich sind, wodurch die Menge an Programmcode erheblich reduziert wird. Die Kraft der Rekursion liegt darin, unendliche Mengen von Objekten mit endlichen Aussagen zu definieren.

Im Allgemeinen erfordert die Rekursion Randbedingungen, einen rekursiven Vorwärtsabschnitt und einen rekursiven Rückkehrabschnitt. Wenn die Randbedingungen nicht erfüllt sind, schreitet die Rekursion voran; wenn die Randbedingungen erfüllt sind, kehrt die Rekursion zurück.

Beispiel für einen verschachtelten Funktionsaufrufprozess

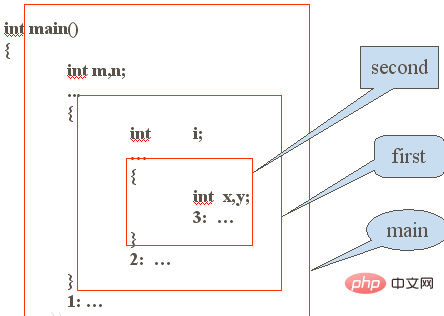
Erforderliche Bedingungen für eine Rekursion:

1 . Das Unterproblem muss dasselbe wie das ursprüngliche Problem sein und einfacher sein -Rekursive Situationsverarbeitung.

In der Mathematik und Informatik bezieht sich Rekursion auf eine Klasse von Objekten oder Methoden, die durch einen (oder mehrere) einfache Basisfälle definiert sind, mit der Bedingung, dass alle anderen Fälle auf ihre Basisfälle reduziert werden können . In der Mathematik und Informatik bezieht sich Rekursion auf eine Klasse von Objekten oder Methoden, die durch einen (oder mehrere) einfache Basisfälle definiert sind, mit der Maßgabe, dass alle anderen Fälle auf ihre Basisfälle reduziert werden können.

Das Folgende ist beispielsweise die rekursive Definition des Vorfahren einer Person: Die Eltern einer Person sind ihre Vorfahren (Basisfall).

Die Eltern eines Vorfahren sind auch die Vorfahren einer anderen Person (rekursiver Schritt). Die Fibonacci-Folge, auch als Goldene-Schnitt-Folge bekannt, bezieht sich auf eine solche Folge: 1, 1, 2, 3, 5, 8, 13, 21 .... I [1]

Die Fibonacci-Folge ist Ein typischer Fall einer Rekursion: Eine rekursive Beziehung liegt vor, wenn eine Entität eine Beziehung zu sich selbst aufbaut.

Fib(0) = 1 [Basisfall] Fib(1) = 1 [Basisfall] Für alle ganzen Zahlen n > 1: Fib(n) = (Fib(n-1) + Fib( n- 2)) [Rekursive Definition] Obwohl viele mathematische Funktionen rekursiv ausgedrückt werden können, ist der hohe Aufwand der rekursiven Definition in praktischen Anwendungen oft unerschwinglich. Zum Beispiel:

Fakultät (1) = 1 [Grundfall] Für alle ganzen Zahlen n > 1: Fakultät (n) = (n * Fakultät (n-1)) [Rekursive Definition] Eine leicht verständliche Definition Das mentale Modell besteht darin, dass rekursive Definitionen Objekte anhand „zuvor definierter“ Objekte desselben Typs definieren. Zum Beispiel: Wie kann man 100 Kartons bewegen? Antwort: Sie verschieben zunächst eine Kiste und notieren, wohin sie verschoben wird, und gehen dann zum kleineren Problem über: Wie können Sie 99 Kisten verschieben? Irgendwann besteht Ihr Problem darin, wie man eine Kiste bewegt, und Sie wissen bereits, wie das geht.

Eine solche Definition ist in der Mathematik sehr verbreitet. Die formale Definition natürlicher Zahlen in der Mengenlehre lautet beispielsweise: 1 ist eine natürliche Zahl, und jede natürliche Zahl hat einen Nachfolger, der ebenfalls eine natürliche Zahl ist.

Der Droste-Effekt

Der Droste-Effekt ist eine visuelle Form der Rekursion. Unter den Gegenständen, die die Frau hält, befindet sich ein kleines Bild von ihr selbst, wie sie denselben Gegenstand hält, und dann gibt es ein noch kleineres Bild von ihr, wie sie denselben Gegenstand hält, und so weiter. Ein anderes Beispiel: Wenn wir eine brennende Kerze zwischen zwei gegenüberliegende Spiegel stellen, sehen wir eine Kerze in einem der Spiegel, und hinter der Kerze befindet sich ein weiterer Spiegel, und im Spiegel befindet sich eine weitere Kerze. Kerzen ... auch das ist eine Manifestation der Rekursion.

Weitere Informationen zu diesem Thema finden Sie auf der

PHP-Website für Chinesisch

! !

Das obige ist der detaillierte Inhalt vonWas ist Rekursion?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!