Implementierung des Heap-Sortierprinzips basierend auf PHP

Heap

Heap ist ein allgemeiner Begriff für eine spezielle Art von Datenstruktur in der Informatik, normalerweise ein Array Objekt, das als Baum betrachtet werden kann.

Haufen {k1,k2,ki,…,kn} (ki <= k2i,ki <= k2i+1)|(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4...n/2)

Über den Heap:

• Der Wert eines Knotens im Heap ist immer Nicht größer oder kleiner als der Wert seines übergeordneten Knotens.
• Der Heap ist immer ein vollständiger Binärbaum (unten).
• Der Heap mit dem größten Wurzelknoten wird als maximaler Heap oder großer Wurzelheap bezeichnet, und der Heap mit dem kleinsten Wurzelknoten wird als minimaler Heap oder kleiner Wurzelheap bezeichnet.

Vollständiger Binärbaum

Wenn es um die Heap-Sortierung geht, müssen wir den vollständigen Binärbaum überall erwähnen wählte die einfachste davon. .

Vollständiger Binärbaum: Mit Ausnahme der letzten Ebene erreicht die Anzahl der Knoten auf jeder Ebene das Maximum; auf der letzten Ebene fehlen nur einige Knoten auf der rechten Seite.

Ich bin zu dem Schluss gekommen, dass dies genau an den folgenden zwei Merkmalen liegt:

• Erlaubt nur, dass die letzte Ebene freie Knoten hat, und die freien Stellen befinden sich auf der rechten Seite, also Blattknoten kann nur auf den beiden größten Ebenen erscheinen (Regelmäßigkeit der Speichermethoden);
• Wenn i>1, ist der übergeordnete Knoten des Baums tree[i p 2] (Regelmäßigkeit seiner übergeordneten und untergeordneten Knotenwerte); 🎜>

macht das Sortieren sehr bequem.

Heap-Sortierung

Heap-Sortierung verwendet den großen oberen Heap für aufsteigende Reihenfolge und den kleinen oberen Heap für absteigende Reihenfolge.

In diesem Beispiel wird zur Analyse ein kleiner oberer Heap in absteigender Reihenfolge verwendet.

Die Schritte für die Heap-Sortierung sind wie folgt:

1 Wir erstellen ein Array $arr aus den Daten (49, 38, 65, 97, 76, 13 , 27, 50) ;

2. Verwenden Sie das Array $arr, um einen kleinen oberen Heap zu erstellen (die Hauptschritte werden in den Codekommentaren erklärt. Das Bild unten zeigt den Prozess der Verwendung eines Arrays zum Erstellen eines kleiner oberer Heap);

3, tauschen Sie die Wurzel des Heaps (das kleinste Element) mit dem letzten Blatt aus, reduzieren Sie die Länge des Heaps um eins und springen Sie zum zweiten Schritt; >4. Wiederholen Sie die Schritte 2-3, bis nur noch ein Knoten im Heap vorhanden ist. Die Sortierung ist abgeschlossen.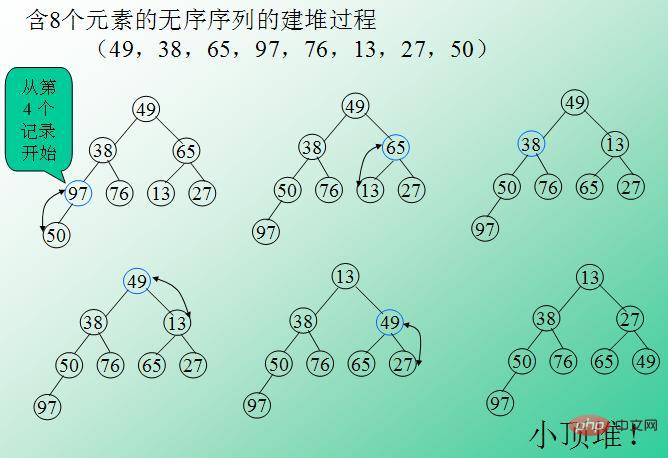

PHP-Implementierung der Heap-Sortierung

//因为是数组,下标从0开始,所以,下标为n根结点的左子结点为2n+1,右子结点为2n+2; 
//初始化值,建立初始堆
$arr=array(49,38,65,97,76,13,27,50);
$arrSize=count($arr);

//将第一次排序抽出来，因为最后一次排序不需要再交换值了。
buildHeap($arr,$arrSize);

for($i=$arrSize-1;$i>0;$i--){
  swap($arr,$i,0);
  $arrSize--;
  buildHeap($arr,$arrSize);  
}

//用数组建立最小堆
function buildHeap(&$arr,$arrSize){
  //计算出最开始的下标$index,如图,为数字"97"所在位置,比较每一个子树的父结点和子结点,将最小值存入父结点中
  //从$index处对一个树进行循环比较,形成最小堆
  for($index=intval($arrSize/2)-1; $index>=0; $index--){
    //如果有左节点,将其下标存进最小值$min
    if($index*2+1<$arrSize){
      $min=$index*2+1;
      //如果有右子结点,比较左右结点的大小,如果右子结点更小,将其结点的下标记录进最小值$min
      if($index*2+2<$arrSize){
        if($arr[$index*2+2]<$arr[$min]){
          $min=$index*2+2;
        }
      }
      //将子结点中较小的和父结点比较,若子结点较小,与父结点交换位置,同时更新较小
      if($arr[$min]<$arr[$index]){
        swap($arr,$min,$index);
      }  
    }
  }
}

//此函数用来交换下数组$arr中下标为$one和$another的数据
function swap(&$arr,$one,$another){
  $tmp=$arr[$one];
  $arr[$one]=$arr[$another];
  $arr[$another]=$tmp;
}

Das Folgende ist das Endergebnis der sort:

Heap wird für die vollständige Sortierung verwendet, und die Zeitkomplexität beträgt O(nlogn)

Und die schnelle Sortierung wird für die vollständige Sortierung verwendet Die durchschnittliche Zeitkomplexität beträgt ebenfalls O(nlogn)

Aber wenn die Heap-Sortierung verwendet werden kann, um TopK zu finden, beträgt die Zeitkomplexität des Heaps O(Klog2(n), da nur K Sortierrunden erforderlich sind.

Empfohlenes Tutorial:《

PHP

》

Das obige ist der detaillierte Inhalt vonImplementierung des Heap-Sortierprinzips basierend auf PHP. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!