Die Beziehung zwischen ausgeglichenen Binärbäumen und binär sortierten Bäumen
Es gibt keine direkte Beziehung zwischen ausgeglichenen Binärbäumen und binären Sortierbäumen, aber die Sucheffizienz binärer Sortierbäume hängt von der Form des Binärbaums ab, also davon, wann wir die Form des binären Sortierbaums haben wollen Seien Sie einheitlich, so werden Binärbäume als ausgeglichene Binärbäume bezeichnet.

1. Binärer Sortierbaum
Binärer Sortierbaum, auch bekannt als Binärer Suchbaum (Binärer Suchbaum), auch bekannt als Binärer Suchbaum.
- Definition des binären Sortierbaums:
Ein binärer Sortierbaum ist entweder ein leerer Baum oder hat die folgenden Eigenschaften: Binärer Baum:
- Wenn der linke Teilbaum nicht leer ist, sind die Werte aller Knoten im linken Teilbaum kleiner als der Wert seines Wurzelknotens.
- Wenn der rechte Teilbaum leer ist nicht leer, dann sind die Werte aller Knoten im rechten Teilbaum größer als der Wert seines Wurzelknotens
- Der linke und rechte Teilbaum sind ebenfalls binär sortierte Bäume.
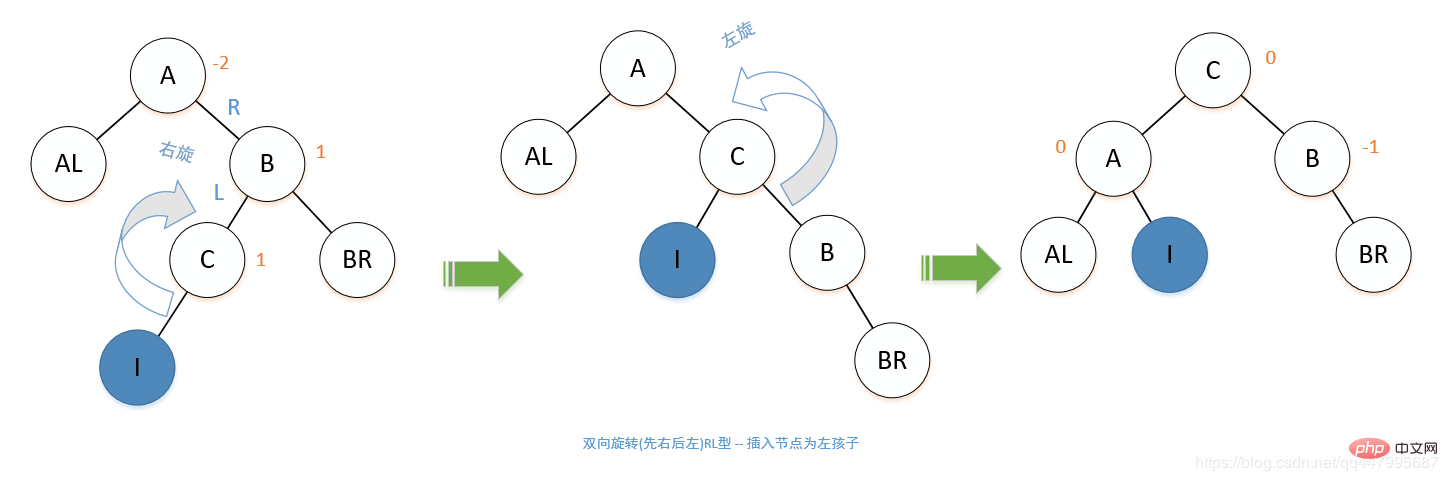
Wie in der Abbildung unten gezeigt, handelt es sich um einen binären Sortierbaum: 
Führen Sie eine Durchquerung des binären Sortierbaums in der richtigen Reihenfolge durch, um eine nach Schlüsselwörtern sortierte Sequenz zu erhalten. Beispielsweise kann eine geordnete Durchquerung der obigen Abbildung eine geordnete Sequenz erhalten: 10, 42, 45, 55, 58, 63, 67, 70, 83, 90, 98
- Suchanalyse des binären Sortierbaums
In Bezug auf die durchschnittliche Zeitleistung der Suche ähnelt die Suche im binären Sortierbaum der binären Suche, jedoch hinsichtlich der Aufrechterhaltung der Ordnungsmäßigkeit der Tabelle In Bezug auf die Effizienz ist der binär sortierte Baum effizienter, da keine Knoten verschoben werden müssen, sondern nur der Zeiger geändert werden muss, um die Einfüge- und Löschvorgänge des binär sortierten Baums abzuschließen.
Binär sortierte Baumsuche Im schlimmsten Fall hängt die benötigte Suchzeit von der Tiefe des Baums ab:
- Wenn ein binärer Sortierbaum nahe an einem vollständigen Binärbaum liegt, beträgt seine Tiefe , also ist die Suchzeit im ungünstigsten Fall O( ), was in der gleichen Größenordnung wie die binäre Suche liegt.
- Wenn ein Binärbaum einen Einzelzweigbaum bildet, wie in der folgenden Abbildung gezeigt, beträgt seine Tiefe n und die Suchzeit beträgt im schlimmsten Fall O (n). in der gleichen Größenordnung wie die sequentielle Suche.

AlsoUm eine hohe Suchgeschwindigkeit für die Suche nach binären Sortierbäumen sicherzustellen, hoffen wir, dass der Binärbaum einem vollständigen Binärbaum nahe kommt oder dass die Tiefen des linken und rechten Teilbaums Jeder Knoten des Binärbaums ist so gleich wie möglich Der Sortierbaum hängt mit der Form des Binärbaums zusammen. Wir hoffen, dass die Form des Binärsortierbaums einheitlich ist. Ein solcher Binärbaum wird als ausgeglichener Binärbaum bezeichnet.-
Definition eines ausgeglichenen Binärbaums
Ausgeglichener Binärbaum (Balanced Binary Tree), es ist ein leerer Baum oder hat die folgenden Eigenschaften:
- Der absolute Wert der Tiefendifferenz zwischen seinem linken und rechten Teilbaum überschreitet nicht 1;
- Sein linker und rechter Teilbaum sind ebenfalls ausgeglichene Binärbäume.
Die Tiefe des linken Teilbaums eines Binärbaumknotens abzüglich der Tiefe seines rechten Teilbaums wird als Balance-Faktor BF bezeichnet, dann ist es nur möglich, die Balance-Faktoren auszubalancieren aller Knoten im Binärbaum sind -1, 0 und 1. Der linke in der Abbildung unten ist ein ausgeglichener Binärbaum und der rechte ist ein unausgeglichener Binärbaum.

Da der Unterschied zwischen den Tiefen des linken und rechten Teilbaums eines beliebigen Knotens in einem ausgeglichenen Binärbaum 1 nicht überschreitet, kann bewiesen werden, dass seine Tiefe mit der Tiefe eines vollständigen Knotens übereinstimmt Binärbaum mit n Knoten +1 sind gleich Größenordnung. Daher beträgt die durchschnittliche Anzahl der Suchanfragen auch >g2g -
Definition eines ausgeglichenen Binärbaums
Das obige ist der detaillierte Inhalt vonDie Beziehung zwischen ausgeglichenen Binärbäumen und binär sortierten Bäumen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1381
1381
 52
52




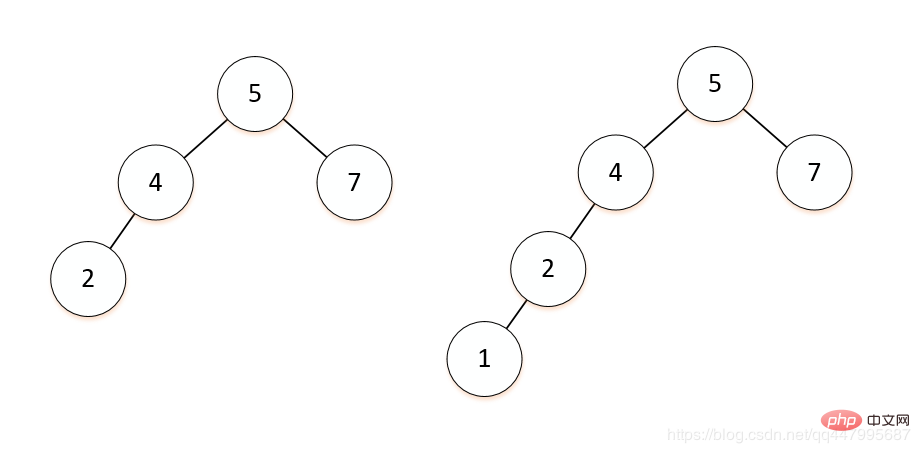
 Die Einfügeposition ist der rechte Teilbaum des rechten Teilbaums und der rechte Teilbaum ist die Achse, und eine einzelne Operation wird ausgeführt.
Die Einfügeposition ist der rechte Teilbaum des rechten Teilbaums und der rechte Teilbaum ist die Achse, und eine einzelne Operation wird ausgeführt.  Das Prinzip ist das gleiche wie in RR Beim LR-Typ liegt das R-Ende oder L in der Nähe des eingefügten Knotenendes als Rotationsachse (wie in der Abbildung unten gezeigt, entspricht dies dem Drehen des Teilbaums zuerst mit B als Wurzel und dem anschließenden Drehen des Teilbaums mit A als Wurzel und dann den Teilbaum mit A als Wurzel drehen. Untergeordnetes Element:
Das Prinzip ist das gleiche wie in RR Beim LR-Typ liegt das R-Ende oder L in der Nähe des eingefügten Knotenendes als Rotationsachse (wie in der Abbildung unten gezeigt, entspricht dies dem Drehen des Teilbaums zuerst mit B als Wurzel und dem anschließenden Drehen des Teilbaums mit A als Wurzel und dann den Teilbaum mit A als Wurzel drehen. Untergeordnetes Element: