N Algorithmen für die Fibonacci-Sequenz in PHP-PHP-Tutorial-php.cn

N Algorithmen für die Fibonacci-Sequenz in PHP

藏色散人

Freigeben： 2023-04-09 14:46:01

nach vorne

4417 Leute haben es durchsucht

N Algorithmen für die Fibonacci-Sequenz in PHP

Vorwort

Vor einiger Zeit bin ich auf die herkömmliche rekursive Methode zur Optimierung der Berechnung von Fibonacci-Zahlen gestoßen, aber mir fiel nicht rechtzeitig eine gute Methode ein, also suchte ich später nach relevanten Informationen und Vieles zusammengefasst Es gibt eine Berechnungslösung, also teilen Sie sie und kommunizieren und lernen Sie mit allen.

Empfohlen: „PHP Video Tutorial“

Was sind Fibonacci-Zahlen? daher wird sie auch „Kaninchenfolge“ genannt, was sich auf eine solche Folge bezieht: 1, 1, 2, 3, 5, 8, 13, 21, 34,… …Mathematisch ist die Fibonacci-Folge rekursiv wie folgt definiert: F (1)=1, F(2)=1, F(n)=F(n - 1)+F(n - 2) (n ≥ 3, n ∈ N*).

Da wir nun die Fibonacci-Zahlen kennen, werden wir verschiedene Methoden verwenden, um die N-te Fibonacci-Zahl zu berechnen und zu erhalten.

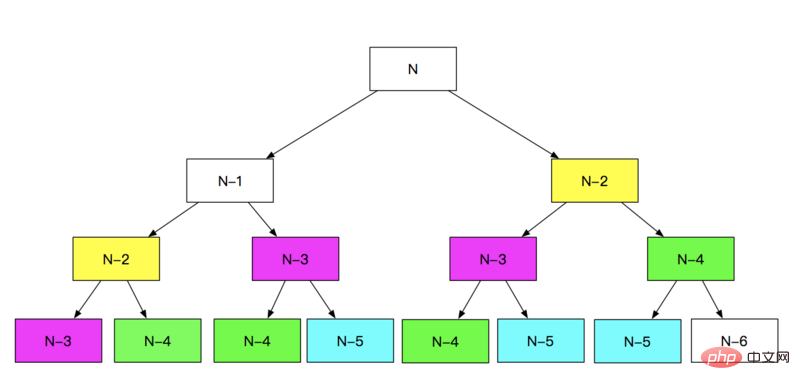
Gewöhnliche Rekursion

斐波那契数，那么下面我们就用多种不同的方法来计算获取第N位斐波那契数。

普通递归

这种方法是最常规的，直接根据定义F(n)=F(n - 1)+F(n - 2)递归计算即可，但是性能是最低的。

/**
 * 普通递归
 * @param int $n
 * @return int
 */function fib($n = 1){    // 低位处理
    if ($n < 3) {        return 1;
    }    // 递归计算前两位
    return fib($n - 1) + fib($n - 2);
}

Nach dem Login kopieren

递归优化

从上面的递归方法可以看到，进行了很多的重复计算，性能极差，如果N越大，计算的次数太可怕了，那么，既然因为重复计算影响了性能，那么优化就从减少重复计算入手，即把之前计算的存储起来，这样就避免了过多的重复计算，优化了递归算法。

/**
 * 递归优化
 * @param int $n
 * @param int $a
 * @param int $b
 * @return int
 */function fib_2($n = 1, $a = 1, $b = 1){    if ($n > 2) {        // 存储前一位，优化递归计算
        return fib_2($n - 1, $a + $b, $a);
    }    return $a;
}

Nach dem Login kopieren

记忆化自底向上

自底向上通过迭代计算斐波那契数的子问题并存储已计算的值，通过已计算的值进行计算。使用for循环，减少递归带来的重复计算问题。

/**
 * 记忆化自底向上
 * @param int $n
 * @return int
 */function fib_3($n = 1){
    $list = [];    for ($i = 0; $i <= $n; $i++) {        // 从低到高位数，依次存入数组中
        if ($i < 2) {
            $list[] = $i;
        } else {
            $list[] = $list[$i - 1] + $list[$i - 2];
        }
    }    // 返回最后一个数，即第N个数
    return $list[$n];
}

Nach dem Login kopieren

自底向上进行迭代

最低位初始化赋值，使用for从低位到高位迭代计算，从而得到第N个数。

/**
 * 自底向上进行迭代
 * @param int $n
 * @return int
 */function fib_4($n = 1){    // 低位处理
    if ($n <= 0) {        return 0;
    }    if ($n < 3) {        return 1;
    }
    $a = 0;
    $b = 1;    // 循环计算
    for ($i = 2; $i < $n; $i++) {
        $b = $a + $b;
        $a = $b - $a;
    }    return $b;
}

Nach dem Login kopieren

公式法

通过了解斐波那契序列和黄金分割比之间的关系，使用黄金分割率计算第N

Diese Methode ist die konventionellste. Sie kann rekursiv gemäß der Definition F(n)=F(n - 1)+F(n - 2) berechnet werden. aber die Leistung ist minimal.

/**
 * 公式法
 * @param int $n
 * @return int
 */function fib_5($n = 1){    // 黄金分割比
    $radio = (1 + sqrt(5)) / 2;    // 斐波那契序列和黄金分割比之间的关系计算
    $num = intval(round(pow($radio, $n) / sqrt(5)));    return $num;
}

Nach dem Login kopieren

Rekursive Optimierung

Wie Sie der obigen rekursiven Methode entnehmen können, werden viele Berechnungen wiederholt und die Leistung ist extrem schlecht. Wenn N größer ist, ist die Anzahl der Berechnungen zu schrecklich Da sich wiederholte Berechnungen auf die Leistung auswirken, beginnt die Optimierung mit der Reduzierung wiederholter Berechnungen, d. h. dem Speichern der vorherigen Berechnungen, wodurch zu viele wiederholte Berechnungen vermieden und der rekursive Algorithmus optimiert werden.