Einführung in einige gängige Grundalgorithmen in JS

Ein Algorithmus ist nur eine Funktion, die die Eingabe einer bestimmten Datenstruktur in die Ausgabe einer bestimmten Datenstruktur umwandelt. Die interne Logik des Algorithmus bestimmt, wie konvertiert wird.
Grundlegender Algorithmus
1. Blasensortierung
//冒泡排序function bubbleSort(arr) {
for(var i = 1, len = arr.length; i < len - 1; ++i) {
for(var j = 0; j <= len - i; ++j) {
if (arr[j] > arr[j + 1]) {
let temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}Wenn das Ziel aufsteigt Bei der Sortierung ist das Original am besten geeignet Sequenz Es ist bereits in aufsteigender Reihenfolge sortiert, sodass nur n-1 Mal verglichen werden muss und die zeitliche Komplexität O (n) beträgt. Das schlimmste Szenario besteht darin, dass die Sequenz ursprünglich in absteigender Reihenfolge sortiert ist, sodass n(n-1)/2-mal verglichen werden müssen und die zeitliche Komplexität O(n^2) beträgt. Im Durchschnitt beträgt die zeitliche Komplexität der Einfügesortierung also O(n^2). Offensichtlich ist die Einfügungssortierung aufgrund der zeitlichen Komplexität auf Leistungsebene nicht für Situationen geeignet, in denen viele Daten vorhanden sind. Im Allgemeinen eignet sich die Einfügungssortierung zum Sortieren kleiner Datenmengen. 3. Schnelle Sortierung durch Pivot, Die Textbeschreibung der schnellen Sortierung ist implementiert, was bedeutet, dass es bei der Implementierung des Algorithmus kein Problem gibt.
Obwohl diese Implementierungsmethode sehr einfach zu verstehen ist. Allerdings gibt es auch bei dieser Implementierung Raum für Verbesserungen. Bei dieser Implementierung haben wir festgestellt, dass innerhalb der Funktion zwei Arrays links/rechts definiert sind, um temporäre Daten zu speichern. Mit zunehmender Anzahl von Rekursionen werden immer mehr temporäre Daten definiert und gespeichert, was Ω(n) zusätzlichen Speicherplatz erfordert. Daher wird, wie bei vielen Algorithmuseinführungen, die In-Place-Partitionierungsversion verwendet, um eine schnelle Sortierung zu implementieren. Lassen Sie uns zunächst vorstellen, was ein In-Place-Partitionierungsalgorithmus ist.
Beschreibung des In-Place-PartitionierungsalgorithmusWählen Sie ein Element aus dem Array aus, das als „Pivot“ bezeichnet wird. Die Position des ersten Elements des Arrays wird als Index verwendet.
Durchlaufen Sie das Array. Wenn die Array-Nummer kleiner oder gleich dem Basiswert ist, tauschen Sie die Zahl an der Indexposition durch die Zahl und den Index +1 aus.
Tauschen Sie den Basiswert durch die aktuelle Indexposition
Durch die oben genannten drei Schritte wird der Basiswert zentriert und die Zahlen auf der linken und rechten Seite des Arrays werden kleiner bzw. größer als der Basiswert. Zu diesem Zeitpunkt kann das sortierte Array durch rekursive Partitionierung an Ort und Stelle erhalten werden.
Implementierung des In-Place-Partitionierungsalgorithmus//插入排序 过程就像你拿到一副扑克牌然后对它排序一样 function insertionSort(arr) { var n = arr.length; // 我们认为arr[0]已经被排序,所以i从1开始 for (var i = 1; i < n; i++) { // 取出下一个新元素,在已排序的元素序列中从后向前扫描来与该新元素比较大小 for (var j = i - 1; j >= 0; j--) { if (arr[i] >= arr[j]) { // 若要从大到小排序,则将该行改为if (arr[i] <= arr[j])即可 // 如果新元素arr[i] 大于等于 已排序的元素序列的arr[j], // 则将arr[i]插入到arr[j]的下一位置,保持序列从小到大的顺序 arr.splice(j + 1, 0, arr.splice(i, 1)[0]); // 由于序列是从小到大并从后向前扫描的,所以不必再比较下标小于j的值比arr[j]小的值,退出循环 break; } else if (j === 0) { // arr[j]比已排序序列的元素都要小,将它插入到序列最前面 arr.splice(j, 0, arr.splice(i, 1)[0]); } } } return arr; }Nach dem Login kopierenDa wir mehrere Male direkt rekursiv partitionieren müssen und gleichzeitig keinen zusätzlichen Adressraum wünschen, gibt es bei der Implementierung der Partitionierung drei Parameter Algorithmus, der das ursprüngliche Array-Array, der Startpunkt links vom Array, der durchlaufen werden muss, und der Endpunkt des Arrays, der rechts durchlaufen werden muss, sind.
Abschließend wird für die nächste Rekursion ein sortierter Indexwert zurückgegeben. Der diesem Index entsprechende Wert muss kleiner als das Array-Element auf der linken Seite des Index und größer als alle Array-Elemente auf der rechten Seite sein. Grundsätzlich können wir den Partitionierungsalgorithmus weiter optimieren. Wir haben festgestellt, dass <=pivot in
- Implementierung der schnellen Sortierung der In-Place-Partitionsversion
//快速排序 function qSort(arr) { //声明并初始化左边的数组和右边的数组 var left = [], right = []; //使用数组第一个元素作为基准值 var base = arr[0]; //当数组长度只有1或者为空时,直接返回数组,不需要排序 if(arr.length <= 1) return arr; //进行遍历 for(var i = 1, len = arr.length; i < len; i++) { if(arr[i] <= base) { //如果小于基准值,push到左边的数组 left.push(arr[i]); } else { //如果大于基准值,push到右边的数组 right.push(arr[i]); } } //递归并且合并数组元素 return [...qSort(left), ...[base], ...qSort(right)]; //return qSort(left).concat([base], qSort(right));}Nach dem Login kopieren
2. Zeichenfolge
1. Palindrom-Zeichenfolge
// 交换数组元素位置
function swap(array, i, j) {
var temp = array[i];
array[i] = array[j];
array[j] = temp;
}
function partition(array, left, right) {
var index = left;
var pivot = array[right]; // 取最后一个数字当做基准值,这样方便遍历
for (var i = left; i < right; i++) {
if (array[i] <= pivot) {
swap(array, index, i);
index++;
}
}
swap(array, right, index);
return index;
}3. Array
1. Array-Deduplizierung4. Binäre Suche
rrree Binäre Suche auf die vorherige Einfügungssortierung anwenden, um die Effizienz zu verbessern. Aber als ich es getestet habe, war die Datenmenge vielleicht zu klein und ich konnte keine allzu offensichtliche Lücke finden. . Sie können es selbst ausprobieren ~ (verwenden Sie beispielsweise console.time('Einfügesortierung zeitaufwändig') und console.timeEnd('Einfügesortierung zeitaufwändig') am Anfang und Ende des Funktionsaufrufs)
5. Suchanlage/Durchlauf
1.
Filter ist auch eine häufig verwendete Operation, mit der bestimmte Elemente eines Arrays herausgefiltert und die verbleibenden Elemente zurückgegeben werden. Dies kann auch so verstanden werden: Die Rückruffunktion des Filters verarbeitet jedes Element des Arrays. Wenn das Verarbeitungsergebnis „false“ zurückgibt, entfernt das Filterergebnis das Element () liegt der Schlüssel darin, eine „Filter“-Funktion korrekt zu implementieren. Tatsächlich verfügt diese Filterfunktion über mehrere Parameter, filter(function (element, index, self)), die die Verwendung von Filter zum Entfernen von Duplikaten demonstrieren, wie folgt: function quickSort(array) {
function swap(array, i, j) {
var temp = array[i];
array[i] = array[j];
array[j] = temp;
}
function partition(array, left, right) {
var index = left;
var pivot = array[right]; // 取最后一个数字当做基准值,这样方便遍历
for (var i = left; i < right; i++) {
if (array[i] < pivot) {
swap(array, index, i);
index++;
}
}
swap(array, right, index);
return index;
}
function sort(array, left, right) {
if (left > right) {
return;
}
var storeIndex = partition(array, left, right);
sort(array, left, storeIndex - 1);
sort(array, storeIndex + 1, right);
}
sort(array, 0, array.length - 1);
return array;
}
排序也是在程序中经常用到的算法。无论使用冒泡排序还是快速排序,排序的核心是比较两个元素的大小。如果是数字,我们可以直接比较,但如果是字符串或者两个对象呢?
直接比较数学上的大小是没有意义的,因此,比较的过程必须通过函数抽象出来。通常规定,对于两个元素x和y,如果认为x < y,则返回-1,如果认为x == y,则返回0,如果认为x > y,则返回1,这样,排序算法就不用关心具体的比较过程,而是根据比较结果直接排序。
值得注意的例子:
// 看上去正常的结果: ['Google', 'Apple', 'Microsoft'].sort(); // ['Apple', 'Google', 'Microsoft']; // apple排在了最后: ['Google', 'apple', 'Microsoft'].sort(); // ['Google', 'Microsoft", 'apple'] // 无法理解的结果: [10, 20, 1, 2].sort(); // [1, 10, 2, 20]
解释原因
第二个排序把apple排在了最后,是因为字符串根据ASCII码进行排序,而小写字母a的ASCII码在大写字母之后。
第三个排序结果,简单的数字排序都能错。
这是因为Array的sort()方法默认把所有元素先转换为String再排序,结果’10’排在了’2’的前面,因为字符’1’比字符’2’的ASCII码小。
因此我们把结合这个原理:
var arr = [10, 20, 1, 2];
arr.sort(function (x, y) {
if (x < y) {
return -1;
}
if (x > y) {
return 1;
} return 0;
});
console.log(arr); // [1, 2, 10, 20]上面的代码解读一下:传入x,y,如果x
还有一个,sort()方法会直接对Array进行修改,它返回的结果仍是当前Array,一个例子:
var a1 = ['B', 'A', 'C'];var a2 = a1.sort();
a1; // ['A', 'B', 'C']
a2; // ['A', 'B', 'C']
a1 === a2; // true, a1和a2是同一对象相关免费学习推荐:js视频教程
Das obige ist der detaillierte Inhalt vonEinführung in einige gängige Grundalgorithmen in JS. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 CLIP-BEVFormer: Überwacht explizit die BEVFormer-Struktur, um die Leistung der Long-Tail-Erkennung zu verbessern
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Überwacht explizit die BEVFormer-Struktur, um die Leistung der Long-Tail-Erkennung zu verbessern
Mar 26, 2024 pm 12:41 PM
Oben geschrieben und das persönliche Verständnis des Autors: Derzeit spielt das Wahrnehmungsmodul im gesamten autonomen Fahrsystem eine entscheidende Rolle Das Steuermodul im autonomen Fahrsystem trifft zeitnahe und korrekte Urteile und Verhaltensentscheidungen. Derzeit sind Autos mit autonomen Fahrfunktionen in der Regel mit einer Vielzahl von Dateninformationssensoren ausgestattet, darunter Rundumsichtkamerasensoren, Lidar-Sensoren und Millimeterwellenradarsensoren, um Informationen in verschiedenen Modalitäten zu sammeln und so genaue Wahrnehmungsaufgaben zu erfüllen. Der auf reinem Sehen basierende BEV-Wahrnehmungsalgorithmus wird von der Industrie aufgrund seiner geringen Hardwarekosten und einfachen Bereitstellung bevorzugt, und seine Ausgabeergebnisse können problemlos auf verschiedene nachgelagerte Aufgaben angewendet werden.
 Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Implementierung von Algorithmen für maschinelles Lernen in C++: Häufige Herausforderungen und Lösungen
Jun 03, 2024 pm 01:25 PM
Zu den häufigsten Herausforderungen, mit denen Algorithmen für maschinelles Lernen in C++ konfrontiert sind, gehören Speicherverwaltung, Multithreading, Leistungsoptimierung und Wartbarkeit. Zu den Lösungen gehören die Verwendung intelligenter Zeiger, moderner Threading-Bibliotheken, SIMD-Anweisungen und Bibliotheken von Drittanbietern sowie die Einhaltung von Codierungsstilrichtlinien und die Verwendung von Automatisierungstools. Praktische Fälle zeigen, wie man die Eigen-Bibliothek nutzt, um lineare Regressionsalgorithmen zu implementieren, den Speicher effektiv zu verwalten und leistungsstarke Matrixoperationen zu nutzen.
 Entdecken Sie die zugrunde liegenden Prinzipien und die Algorithmusauswahl der C++-Sortierfunktion
Apr 02, 2024 pm 05:36 PM
Entdecken Sie die zugrunde liegenden Prinzipien und die Algorithmusauswahl der C++-Sortierfunktion
Apr 02, 2024 pm 05:36 PM
Die unterste Ebene der C++-Sortierfunktion verwendet die Zusammenführungssortierung, ihre Komplexität beträgt O(nlogn) und bietet verschiedene Auswahlmöglichkeiten für Sortieralgorithmen, einschließlich schneller Sortierung, Heap-Sortierung und stabiler Sortierung.
 Kann künstliche Intelligenz Kriminalität vorhersagen? Entdecken Sie die Möglichkeiten von CrimeGPT
Mar 22, 2024 pm 10:10 PM
Kann künstliche Intelligenz Kriminalität vorhersagen? Entdecken Sie die Möglichkeiten von CrimeGPT
Mar 22, 2024 pm 10:10 PM
Die Konvergenz von künstlicher Intelligenz (KI) und Strafverfolgung eröffnet neue Möglichkeiten zur Kriminalprävention und -aufdeckung. Die Vorhersagefähigkeiten künstlicher Intelligenz werden häufig in Systemen wie CrimeGPT (Crime Prediction Technology) genutzt, um kriminelle Aktivitäten vorherzusagen. Dieser Artikel untersucht das Potenzial künstlicher Intelligenz bei der Kriminalitätsvorhersage, ihre aktuellen Anwendungen, die Herausforderungen, denen sie gegenübersteht, und die möglichen ethischen Auswirkungen der Technologie. Künstliche Intelligenz und Kriminalitätsvorhersage: Die Grundlagen CrimeGPT verwendet Algorithmen des maschinellen Lernens, um große Datensätze zu analysieren und Muster zu identifizieren, die vorhersagen können, wo und wann Straftaten wahrscheinlich passieren. Zu diesen Datensätzen gehören historische Kriminalstatistiken, demografische Informationen, Wirtschaftsindikatoren, Wettermuster und mehr. Durch die Identifizierung von Trends, die menschliche Analysten möglicherweise übersehen, kann künstliche Intelligenz Strafverfolgungsbehörden stärken
 Verbesserter Erkennungsalgorithmus: zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern
Jun 06, 2024 pm 12:33 PM
Verbesserter Erkennungsalgorithmus: zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern
Jun 06, 2024 pm 12:33 PM
01Ausblicksübersicht Derzeit ist es schwierig, ein angemessenes Gleichgewicht zwischen Detektionseffizienz und Detektionsergebnissen zu erreichen. Wir haben einen verbesserten YOLOv5-Algorithmus zur Zielerkennung in hochauflösenden optischen Fernerkundungsbildern entwickelt, der mehrschichtige Merkmalspyramiden, Multierkennungskopfstrategien und hybride Aufmerksamkeitsmodule verwendet, um die Wirkung des Zielerkennungsnetzwerks in optischen Fernerkundungsbildern zu verbessern. Laut SIMD-Datensatz ist der mAP des neuen Algorithmus 2,2 % besser als YOLOv5 und 8,48 % besser als YOLOX, wodurch ein besseres Gleichgewicht zwischen Erkennungsergebnissen und Geschwindigkeit erreicht wird. 02 Hintergrund und Motivation Mit der rasanten Entwicklung der Fernerkundungstechnologie wurden hochauflösende optische Fernerkundungsbilder verwendet, um viele Objekte auf der Erdoberfläche zu beschreiben, darunter Flugzeuge, Autos, Gebäude usw. Objekterkennung bei der Interpretation von Fernerkundungsbildern
 Einfaches JavaScript-Tutorial: So erhalten Sie den HTTP-Statuscode
Jan 05, 2024 pm 06:08 PM
Einfaches JavaScript-Tutorial: So erhalten Sie den HTTP-Statuscode
Jan 05, 2024 pm 06:08 PM
JavaScript-Tutorial: So erhalten Sie HTTP-Statuscode. Es sind spezifische Codebeispiele erforderlich. Vorwort: Bei der Webentwicklung ist häufig die Dateninteraktion mit dem Server erforderlich. Bei der Kommunikation mit dem Server müssen wir häufig den zurückgegebenen HTTP-Statuscode abrufen, um festzustellen, ob der Vorgang erfolgreich ist, und die entsprechende Verarbeitung basierend auf verschiedenen Statuscodes durchführen. In diesem Artikel erfahren Sie, wie Sie mit JavaScript HTTP-Statuscodes abrufen und einige praktische Codebeispiele bereitstellen. Verwenden von XMLHttpRequest
 Anwendung von Algorithmen beim Aufbau einer 58-Porträt-Plattform
May 09, 2024 am 09:01 AM
Anwendung von Algorithmen beim Aufbau einer 58-Porträt-Plattform
May 09, 2024 am 09:01 AM
1. Hintergrund des Baus der 58-Portrait-Plattform Zunächst möchte ich Ihnen den Hintergrund des Baus der 58-Portrait-Plattform mitteilen. 1. Das traditionelle Denken der traditionellen Profiling-Plattform reicht nicht mehr aus. Der Aufbau einer Benutzer-Profiling-Plattform basiert auf Data-Warehouse-Modellierungsfunktionen, um Daten aus mehreren Geschäftsbereichen zu integrieren, um genaue Benutzerporträts zu erstellen Und schließlich muss es über Datenplattformfunktionen verfügen, um Benutzerprofildaten effizient zu speichern, abzufragen und zu teilen sowie Profildienste bereitzustellen. Der Hauptunterschied zwischen einer selbst erstellten Business-Profiling-Plattform und einer Middle-Office-Profiling-Plattform besteht darin, dass die selbst erstellte Profiling-Plattform einen einzelnen Geschäftsbereich bedient und bei Bedarf angepasst werden kann. Die Mid-Office-Plattform bedient mehrere Geschäftsbereiche und ist komplex Modellierung und bietet allgemeinere Funktionen. 2.58 Benutzerporträts vom Hintergrund der Porträtkonstruktion im Mittelbahnsteig 58
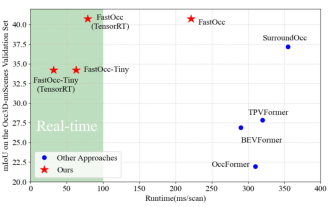 Fügen Sie SOTA in Echtzeit hinzu und explodieren Sie! FastOcc: Schnellere Inferenz und ein einsatzfreundlicher Occ-Algorithmus sind da!
Mar 14, 2024 pm 11:50 PM
Fügen Sie SOTA in Echtzeit hinzu und explodieren Sie! FastOcc: Schnellere Inferenz und ein einsatzfreundlicher Occ-Algorithmus sind da!
Mar 14, 2024 pm 11:50 PM
Oben geschrieben & Das persönliche Verständnis des Autors ist, dass im autonomen Fahrsystem die Wahrnehmungsaufgabe eine entscheidende Komponente des gesamten autonomen Fahrsystems ist. Das Hauptziel der Wahrnehmungsaufgabe besteht darin, autonome Fahrzeuge in die Lage zu versetzen, Umgebungselemente wie auf der Straße fahrende Fahrzeuge, Fußgänger am Straßenrand, während der Fahrt angetroffene Hindernisse, Verkehrszeichen auf der Straße usw. zu verstehen und wahrzunehmen und so flussabwärts zu helfen Module Treffen Sie richtige und vernünftige Entscheidungen und Handlungen. Ein Fahrzeug mit autonomen Fahrfähigkeiten ist in der Regel mit verschiedenen Arten von Informationserfassungssensoren ausgestattet, wie z. B. Rundumsichtkamerasensoren, Lidar-Sensoren, Millimeterwellenradarsensoren usw., um sicherzustellen, dass das autonome Fahrzeug die Umgebung genau wahrnehmen und verstehen kann Elemente, die es autonomen Fahrzeugen ermöglichen, beim autonomen Fahren die richtigen Entscheidungen zu treffen. Kopf






