Der Unterschied zwischen zeitvariablen Systemen und zeitinvarianten Systemen: Ein oder mehrere Parameterwerte in einem zeitvariablen System ändern sich mit der Zeit, sodass sich auch die gesamten Eigenschaften mit der Zeit ändern Ändern Sie sich nicht mit der Zeit. Das Verhalten der Systemreaktion hängt nur vom Verhalten des Eingangssignals und den Eigenschaften des Systems ab und hat nichts mit der Zeit zu tun, zu der das Eingangssignal angelegt wird.
Die Betriebsumgebung dieses Tutorials: Windows 7-System, Dell G3-Computer.
Je nachdem, ob das System Komponenten enthält, deren Parameter sich mit der Zeit ändern, können automatische Steuerungssysteme in zwei Kategorien eingeteilt werden: zeitveränderliche Systeme und stetige Systeme.
Ein stabiles System wird auch als zeitinvariantes System bezeichnet. Seine Eigenschaften sind: Die systemeigenen Eigenschaften (wesentliche Eigenschaften des untersuchten Objekts wie Masse, Trägheitsmoment usw.) ändern sich nicht mit der Zeit . Insbesondere hängt das Verhalten der Systemreaktion nur vom Verhalten des Eingangssignals und den Eigenschaften des Systems ab und hat nichts mit dem Zeitpunkt zu tun, zu dem das Eingangssignal angelegt wird. Das heißt, wenn das Eingangssignal u(t) erzeugt die Ausgabe y(t), dann ist die von u(t-τ) erzeugte Ausgabe y(t-τ), wenn die Eingabe verzögert wird. Nachdem τ auf das System angewendet wurde.
Stetiges System wird auch zeitinvariantes System genannt
Das heißt: Die systemeigenen Eigenschaften ändern sich mit der Zeit nicht. Konkret hängt das Verhalten der Systemreaktion nur vom Verhalten des Eingangssignals und den Eigenschaften des Systems ab und hat nichts mit dem Zeitpunkt zu tun, zu dem das Eingangssignal angelegt wird. Das heißt, ich gebe u bei t1 ein und die Ausgabe ist y. Dann gebe ich u bei t2 ein und der Ausgabewert ist immer noch y
Zeitvariables System
wobei ein oder mehrere Parameterwerte Ändern sich mit der Zeit, und somit ändern sich die gesamten Eigenschaften des Systems im Laufe der Zeit.
Eine Rakete ist ein typisches Beispiel für ein zeitveränderliches System. Während des Fluges nimmt ihre Masse aufgrund des Treibstoffverbrauchs ab Bewegung ist eine komplexe Funktion mit der Zeit als unabhängiger Variable.
Ein zeitinvariantes System ist ein System, dessen Ausgabe sich nicht direkt mit der Zeit ändert.
Wenn das Eingangssignal 
eine Ausgabe y(t) erzeugt, dann erhalten Sie für jede Zeitverzögerung der Eingabe 
eine Ausgabe mit der gleichen Zeitverzögerung 
.
Wenn die Übertragungsfunktion des Systems keine Funktion der Zeit ist, kann diese Eigenschaft erfüllt werden. Diese Funktion kann auch schematisch beschrieben werden
Wenn ein System zeitinvariant ist, dann sind das Systemblockdiagramm und das Blockdiagramm bei jeder Zeitverzögerung austauschbar.
Um zu zeigen, wie man bestimmt, ob ein System zeitinvariant ist, schauen wir uns zwei Systeme an:
System A:
System B:
Da System A zusätzlich zu x(t) und y(t) explizit von t abhängt, ist es ein zeitvariables System, während System B nicht explizit von der Zeit t abhängt und daher zeitinvariant ist .
Mathematische Analyse:
Angenommen, die Eingabe eines bestimmten Systems ist u(t) und die entsprechende Ausgabe ist y(t).
Wenn die Eingabe um τ verzögert ist, das heißt, wenn die Eingabe u(t-τ) ist, wenn die Ausgabe entsprechend um τ verzögert ist, das heißt, die Ausgabe y(t-τ) ist, dann dies Das System ist ein stabiles System.
Das heißt, wenn das Eingangssignal u(t) zuerst um τ auf u(t-τ) verschoben wird und dann die Systemtransformation H[▪] durchgeführt wird, um den Wert H[u(t-τ)] zu erhalten ;
Um es ganz klar auszudrücken: Ein System läuft vom ersten Moment an für einen Zeitraum T und die Eingabe und Ausgabe während dieses Zeitraums weisen eine entsprechende Flugbahn auf.
Wenn der Zustand dieses Systems zum Zeitpunkt T für einen Zeitraum T mit der Anfangszeit erneut ausgeführt wird, ändert sich die Eingabe von der Anfangszeit in die gleiche Form wie zuvor. Überprüfen Sie, ob die Ausgabe der ist wie zuvor
(Am Beispiel einer Rakete bezieht sich die Eingabe auf die Energie des Stoßes und die Ausgabe auf die Beschleunigung;
Das erste Mal, dass die Rakete ist Wenn die Rakete unter normalen Bedingungen gestartet wird und für die Zeit T läuft, können die eingegebene Energie, die Beschleunigung und die Zeit aufgezeichnet werden. Zeichnen Sie eine dreidimensionale Kurve Q1 Beim ersten Mal und beim Laufen für die Zeit T (die Änderung der Eingangsenergie mit der Zeit ist die gleiche wie beim ersten Mal) zeichnen sich zu diesem Zeitpunkt die Eingangsenergie, die Beschleunigungsleistung und die Zeitänderungen um eine weitere dreidimensionale Kurve Q2 Q1 und Q2 überlappen sich nicht in der Ausgangsbeschleunigung (sie wird sich definitiv ändern, da die Masse zum Zeitpunkt T kleiner wird))
und der Eingang Das Signal u(t) durchläuft zunächst die Systemtransformation H[▪], um y zu erhalten (t) und führt dann eine Zeitverschiebung durch, um den gleichen Wert y(t-τ) zu erhalten, d. h. H[u(t-τ)]=y(t-τ). Zum Beispiel: 1. Bestimmen Sie, ob das System y(t)=cos[u(t)], t>0 ein zeitinvariantes System ist: 1). Verschieben Sie nach u(t -τ) und führen Sie dann eine Systemtransformation durch, um den Wert cos[u(t-τ)], t>0, zu erhalten. Führen Sie zunächst eine Systemtransformation in cos[ durch. u(t)], der durch Zeitverschiebung erhaltene Wert ist cos[u(t-τ)], t>0
sind gleich, also ist das System ein zeitinvariantes System.
2. Bestimmen Sie, ob das System y(t)=u(t)▪cost ein zeitinvariantes System ist: 1) Geben Sie das Signal u(t) ein und führen Sie dann eine Zeitverschiebung zu u(t-τ) durch Führen Sie eine Systemtransformation durch. Der erhaltene Wert ist u(t-τ)▪cost, t>0. Eingangssignal u(t), führen Sie zuerst eine Systemtransformation in u(t)▪cost durch und führen Sie dann eine Zeitverschiebung durch, um ihn zu erhalten der Wert u(t-τ)▪cos(t-τ), t>0;
u(t-τ)▪cost≠u(t-τ)▪cos(t-τ), also ist das System eine Zeit -Variierendes System
Als letztes muss überprüft werden, ob die endgültigen Bilder der beiden Pfade (d. h. das Bild in der unteren rechten Ecke) miteinander übereinstimmen
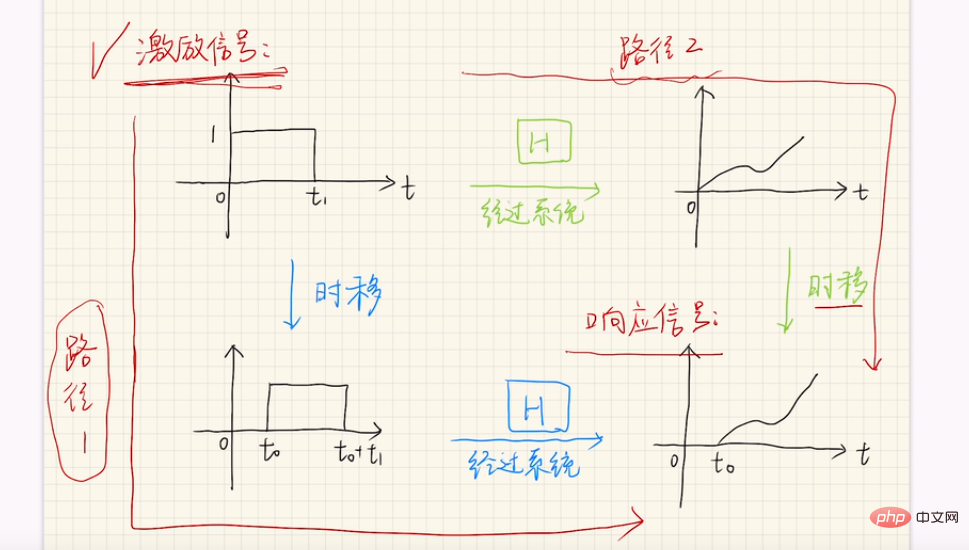Hinweis: Die obige Analyse Die Methode kann auch verwendet werden, um mit der von mir erwähnten Methode zu testen, ob es sich um ein stabiles System handelt, d
Das obige ist der detaillierte Inhalt vonWas ist der Unterschied zwischen zeitvariablen Systemen und zeitinvarianten Systemen?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
