Womit werden Daten in Computern gespeichert und verarbeitet?
Die Speicherung und Verarbeitung von Daten in Computern erfolgt „binär“. Da Binärzahlen nur zwei Grundsymbole haben, „0“ und „1“, und Computer aus logischen Schaltkreisen bestehen, haben logische Schaltkreise normalerweise nur zwei Zustände: Der Schalter ist ein und ausgeschaltet, und für diese beiden kann „1“ verwendet werden Zustände und „0“ zeigt an.

Daten im Computer werden binär dargestellt. Daten in Computern können entsprechend ihrer grundlegenden Verwendung in zwei Kategorien eingeteilt werden: numerische Daten und nicht numerische Daten. Numerische Daten stellen eine bestimmte Größe dar, die in positive und negative Größen unterteilt werden kann. Zu nicht-numerischen Daten gehören hauptsächlich Zeichen, Töne, Bilder usw. Diese Art von Daten muss mithilfe einer bestimmten Kodierungsmethode in eine binäre Darstellung umgewandelt werden, bevor sie im Computer gespeichert und verarbeitet werden kann.
(1) Das Konzept des Basissystems
Das Basissystem ist auch das Tragesystem, eine von Menschen vorgeschriebene Tragemethode. Für jedes Basissystem - X-Basissystem - bedeutet dies, dass die Zahl an einer bestimmten Position bei jeder Berechnung von X um eine Ziffer erhöht wird. Das Dezimalsystem rückt nach jedem Zehntel um eins vor, das Hexadezimalsystem rückt nach jedem Hexadezimal um eins vor, das Binärsystem rückt nach jeweils zwei vor
Wenn in einem Zahlensystem, das Übertragszählung verwendet, nur r Grundsymbole zur Darstellung eines Werts verwendet werden, spricht man von r- Vorwärts. System (Radix-r-Zahlensystem), r wird die Basis (Radix) des Zahlensystems genannt. Die gemeinsamen Merkmale verschiedener Zahlensysteme sind wie folgt:
(1) Jedes Zahlensystem verfügt über einen bestimmten Satz von Symbolen. Das Dezimalzahlensystem hat beispielsweise zehn Grundsymbole: 0,1,2...,9. Es gibt zwei Grundsymbole des binären Zahlensystems: 0 und 1.
(2) Jedes Zahlensystem verwendet eine Positionsdarstellung. Das heißt, die von den Symbolen an verschiedenen Positionen dargestellten Werte sind unterschiedlich, was mit der Gewichtung ihrer Positionen zusammenhängt.
Zum Beispiel: 1234,55 in Dezimalzahl kann ausgedrückt werden als
1234,55=1×10^3+2×10^2+3×10^1+4×10^0+5×10^(-1)+5 ×10^ (-2)
Es ist ersichtlich, dass der Wert des Gewichts in verschiedenen Carry-Zählsystemen genau einer bestimmten Potenz der Basis entspricht. Daher kann jede durch ein Übertragszählsystem dargestellte Zahl als durch Gewichte erweitertes Polynom geschrieben werden.
(2) Warum werden Binärdateien in Computern verwendet?
Die Verwendung von Binärdateien in Computern wird durch den Implementierungsmechanismus bestimmt. Wir können es so verstehen: Die Grundkomponenten eines Computers bestehen aus integrierten Schaltkreisen, und diese integrierten Schaltkreise können als aus Gate-Schaltkreisen zusammengesetzt betrachtet werden (natürlich ist das nicht so einfach).
Wenn der Computer arbeitet, ist der Stromkreis eingeschaltet, sodass an jedem Ausgangsanschluss Spannung anliegt. Der Spannungspegel wird durch Analog-Digital-Umwandlung in Binärwerte umgewandelt: Der hohe Pegel wird durch 1 und der niedrige Pegel durch 0 dargestellt. Das heißt, analoge Schaltkreise in digitale Schaltkreise umwandeln. Der hohe Pegel und der niedrige Pegel können hier künstlich bestimmt werden, wobei der niedrige Pegel unter 2,5 Volt und der hohe Pegel über 3,2 Volt liegt. Elektronische Computer können Informationen mit extrem hoher Geschwindigkeit verarbeiten und verarbeiten. und verfügt über hervorragende Möglichkeiten zur Informationsspeicherung. Daten werden im Computer durch den physischen Zustand des Geräts dargestellt, wobei ein binäres Zahlensystem verwendet wird. Alle vom Computer verarbeiteten Zeichen oder Symbole müssen auch durch binäre Kodierung dargestellt werden. Die Vorteile der Verwendung von Binärdateien bestehen darin, dass sie einfach darzustellen sind, über einfache Betriebsregeln verfügen und Geräte sparen. Es ist bekannt, dass Komponenten mit zwei stabilen Zuständen (z. B. Ein- und Ausschalten von Transistoren, Ein- und Ausschalten von Relais, Pegel elektrischer Impulse usw.) leicht zu finden sind, es ist jedoch erforderlich, Komponenten mit 10 stabilen Zuständen zu finden Dezimal-10-Zahlen sind schwierig
1) Die Technologie ist einfach zu implementieren. Logikschaltungen bestehen normalerweise nur aus zwei Zuständen. Diese beiden Zustände können als „1“ verwendet werden „0“ bedeutet. (2) Vereinfachte Operationsregeln: Es gibt drei Kombinationen von Summen- und Produktoperationen zweier Binärzahlen. Die Operationsregeln sind einfach, was zur Vereinfachung der internen Struktur des Computers und zur Verbesserung der Operationsgeschwindigkeit beiträgt. (3) Geeignet für logische Operationen: Die logische Algebra ist die theoretische Grundlage für logische Operationen. Es gibt nur zwei Ziffern im Binärsystem, was in der logischen Algebra mit „wahr“ und „falsch“ übereinstimmt. (4) Einfach zu konvertieren, Binär- und Dezimalzahlen lassen sich leicht ineinander umwandeln. (5) Die binäre Darstellung von Daten bietet den Vorteil einer starken Entstörungsfähigkeit und einer hohen Zuverlässigkeit. Da jedes Datenbit nur zwei Zustände hat: hoch und niedrig, kann bei einer gewissen Störung immer noch zuverlässig unterschieden werden, ob es hoch oder niedrig ist.
(3), warum erscheinen Oktal- und Hexadezimalzahlen?
Die allgemeine Denkweise des Menschen wird in Dezimalzahlen ausgedrückt, während Computer in Binärzahlen ausgedrückt werden, aber für Programmierer müssen sie alle direkt mit Taschenrechnern umgehen, wenn wir erhalten eine große Folge von Binärzahlen. Zum Beispiel ein 4-Byte-Int-Datentyp: 0000 1010 1111 0101 1000 1111 11111 1111. Ich denke, jeder Programmierer wird sehr verärgert sein, wenn er eine so große Zeichenfolge aus 0 und 1 sieht. Daher muss es eine prägnantere und flexiblere Möglichkeit geben, dieses Datenpaar darzustellen.
Sie können sagen, dass die Verwendung von Dezimalzahlen die Art und Weise des Computerdenkens (binär) nicht genau ausdrücken kann. Tatsächlich werden Hexadezimalzahlen häufiger verwendet, wie oben beschrieben Daten vom Typ int werden direkt in Oktal konvertiert, 32./3 Rest 2 bedeutet, dass wir vorne 0 hinzufügen müssen, aber bei der Konvertierung in Hexadezimal ist es anders. 32/4 = 8, direkt als Zeichenfolge mit 8 Hexadezimalwerten geschrieben, einfach und klar.
Die Verwendung von Hexadezimalzahlen zur Darstellung binärer Zeichenfolgen ist also zweifellos die beste Möglichkeit, weshalb Oktal- und Hexadezimalzahlen vorkommen.
(4), das Problem der gegenseitigen Konvertierung zwischen Basen
Üblicherweise verwendete Basen sind binär, dezimal, oktal und hexadezimal
Konvertierung zwischen binär und dezimal
Dezimal in binär
Die Methode ist: Dezimal Die Restmethode ist zu Teilen Sie eine Zahl durch 2, dh teilen Sie eine Dezimalzahl durch 2, und der Rest ist die Zahl an der Gewichtsposition. Der erhaltene Quotientenwert wird weiterhin durch 2 geteilt und die Operation wird nach unten fortgesetzt, bis der Quotient 0 ist.
(Die spezifische Verwendung ist wie unten gezeigt)

Binär zu Dezimalzahl
Die Methode ist: Erweitern Sie die Binärzahlen entsprechend ihrer Gewichtung und addieren Sie sie, um die Dezimalzahl zu erhalten.
(Die spezifische Verwendung ist wie unten gezeigt)

Konvertierung zwischen Binär und Oktal
Binär in Oktal
Die Methode ist: 3-stellige Binärzahlen werden entsprechend ihrer Gewichtung erweitert und addiert, um eine 1-stellige Zahl zu erhalten Oktalzahl. (Hinweis: Bei der Konvertierung von 3-stelligen Binärzahlen in Oktalzahlen beginnt die Konvertierung von rechts nach links, und 0 wird hinzugefügt, wenn die Zahl nicht ausreicht.)
(Die spezifische Verwendung ist im Bild unten dargestellt)

Oktalzahl in Binärzahl umwandeln
Die Methode lautet: Die Oktalzahl wird durch 2 geteilt und der Rest wird erhalten, und die Binärzahl wird erhalten Für jede Oktalzahl gibt es 3 Binärzahlen. Wenn diese nicht ausreichen, fügen Sie sie zur Null ganz links hinzu. (Die spezifische Verwendung ist wie unten gezeigt) Vier in einem. (Beachten Sie, dass die Konvertierung von 4-stelliger Binärzahl in Hexadezimalzahl von rechts nach links erfolgt und 0 hinzugefügt wird, wenn die Zahl nicht ausreicht.) (Die spezifische Verwendung ist wie unten gezeigt) 4 Binär, falls nicht ausreichend, ganz links Nullen auffüllen.
(Die spezifische Verwendung ist wie unten gezeigt)

Konvertierung zwischen Dezimal-, Oktal- und Hexadezimalzahl
Es gibt zwei Methoden, um Dezimalzahlen in Oktal- oder Hexadezimalzahlen umzuwandeln.
Erste: Indirekte Methode – Dezimalzahl in Binärzahl umwandeln, und dann Konvertieren von binär in oktal oder hexadezimal. Auf die Verwendung von Bildern wird hier nicht mehr näher eingegangen.
Zweitens: Direkte Methode – Konvertieren Sie Dezimalzahlen in Oktal- oder Hexadezimalzahlen, indem Sie durch 8 oder 16 dividieren und den Rest bilden, bis der Quotient 0 ist.
(Die spezifische Verwendung ist wie unten gezeigt) 
Oktal- oder Hexadezimalzahl in Dezimalzahl umwandeln
Die Methode ist: Erweitern Sie die Oktal- und Hexadezimalzahlen entsprechend ihrer Gewichtung und addieren Sie sie, um die Dezimalzahl zu erhalten.
(Die spezifische Verwendung ist wie unten gezeigt) 
Konvertierung zwischen Hexadezimal und Oktal
Es gibt zwei Methoden zur Konvertierung zwischen Oktal und Hexadezimal.
Die erste: Konvertierung zwischen ihnen. Sie kann zuerst in Binär umgewandelt werden dann ineinander umgewandelt.
Zweitens: Die Umrechnung zwischen ihnen kann zuerst in eine Dezimalzahl und dann ineinander umgewandelt werden.
Eine weitere Erklärung zur Verwendung von Bildern erfolgt hier nicht.
Das obige ist der detaillierte Inhalt vonWomit werden Daten in Computern gespeichert und verarbeitet?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
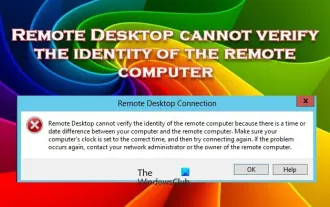 Remotedesktop kann die Identität des Remotecomputers nicht authentifizieren
Feb 29, 2024 pm 12:30 PM
Remotedesktop kann die Identität des Remotecomputers nicht authentifizieren
Feb 29, 2024 pm 12:30 PM
Mit dem Windows-Remotedesktopdienst können Benutzer aus der Ferne auf Computer zugreifen, was für Personen, die aus der Ferne arbeiten müssen, sehr praktisch ist. Es können jedoch Probleme auftreten, wenn Benutzer keine Verbindung zum Remotecomputer herstellen können oder Remotedesktop die Identität des Computers nicht authentifizieren kann. Dies kann durch Netzwerkverbindungsprobleme oder einen Fehler bei der Zertifikatsüberprüfung verursacht werden. In diesem Fall muss der Benutzer möglicherweise die Netzwerkverbindung überprüfen, sicherstellen, dass der Remote-Computer online ist, und versuchen, die Verbindung wiederherzustellen. Außerdem ist es wichtig, sicherzustellen, dass die Authentifizierungsoptionen des Remotecomputers richtig konfiguriert sind, um das Problem zu lösen. Solche Probleme mit den Windows-Remotedesktopdiensten können normalerweise durch sorgfältiges Überprüfen und Anpassen der Einstellungen behoben werden. Aufgrund eines Zeit- oder Datumsunterschieds kann Remote Desktop die Identität des Remotecomputers nicht überprüfen. Bitte stellen Sie Ihre Berechnungen sicher
 Die CSRankings National Computer Science Rankings 2024 sind veröffentlicht! CMU dominiert die Liste, MIT fällt aus den Top 5
Mar 25, 2024 pm 06:01 PM
Die CSRankings National Computer Science Rankings 2024 sind veröffentlicht! CMU dominiert die Liste, MIT fällt aus den Top 5
Mar 25, 2024 pm 06:01 PM
Die 2024CSRankings National Computer Science Major Rankings wurden gerade veröffentlicht! In diesem Jahr gehört die Carnegie Mellon University (CMU) im Ranking der besten CS-Universitäten in den Vereinigten Staaten zu den Besten des Landes und im Bereich CS, während die University of Illinois at Urbana-Champaign (UIUC) einen der besten Plätze belegt sechs Jahre in Folge den zweiten Platz belegt. Georgia Tech belegte den dritten Platz. Dann teilten sich die Stanford University, die University of California in San Diego, die University of Michigan und die University of Washington den vierten Platz weltweit. Es ist erwähnenswert, dass das Ranking des MIT zurückgegangen ist und aus den Top 5 herausgefallen ist. CSRankings ist ein globales Hochschulrankingprojekt im Bereich Informatik, das von Professor Emery Berger von der School of Computer and Information Sciences der University of Massachusetts Amherst initiiert wurde. Die Rangfolge erfolgt objektiv
 Was ist e im Computer?
Aug 31, 2023 am 09:36 AM
Was ist e im Computer?
Aug 31, 2023 am 09:36 AM
Das „e“ von Computer ist das Symbol der wissenschaftlichen Notation. Der Buchstabe „e“ wird als Exponententrennzeichen in der wissenschaftlichen Notation verwendet, was „multipliziert mit der Zehnerpotenz“ bedeutet. In der wissenschaftlichen Notation wird eine Zahl normalerweise als M × geschrieben 10^E, wobei M eine Zahl zwischen 1 und 10 ist und E den Exponenten darstellt.
 Fix: Microsoft Teams-Fehlercode 80090016 Das Trusted Platform-Modul Ihres Computers ist ausgefallen
Apr 19, 2023 pm 09:28 PM
Fix: Microsoft Teams-Fehlercode 80090016 Das Trusted Platform-Modul Ihres Computers ist ausgefallen
Apr 19, 2023 pm 09:28 PM
<p>MSTeams ist die vertrauenswürdige Plattform zum Kommunizieren, Chatten oder Telefonieren mit Teamkollegen und Kollegen. Der Fehlercode 80090016 auf MSTeams und die Meldung <strong>Das Trusted Platform Module Ihres Computers ist fehlgeschlagen</strong> kann zu Schwierigkeiten beim Anmelden führen. Die App erlaubt Ihnen keine Anmeldung, bis der Fehlercode behoben ist. Wenn Sie beim Öffnen von MS Teams oder einer anderen Microsoft-Anwendung auf solche Meldungen stoßen, kann Ihnen dieser Artikel bei der Lösung des Problems helfen. </p><h2&
 Was bedeutet Computer-Cu?
Aug 15, 2023 am 09:58 AM
Was bedeutet Computer-Cu?
Aug 15, 2023 am 09:58 AM
Die Bedeutung von cu in einem Computer hängt vom Kontext ab: 1. Steuereinheit, im Zentralprozessor eines Computers, CU ist die Komponente, die für die Koordinierung und Steuerung des gesamten Rechenprozesses verantwortlich ist. 2. Recheneinheit, in einem Grafikprozessor oder einem anderen Beschleunigter Prozessor, CU ist die Grundeinheit zur Verarbeitung paralleler Rechenaufgaben.
 Das Gruppenrichtlinienobjekt kann auf diesem Computer nicht geöffnet werden
Feb 07, 2024 pm 02:00 PM
Das Gruppenrichtlinienobjekt kann auf diesem Computer nicht geöffnet werden
Feb 07, 2024 pm 02:00 PM
Gelegentlich kann es bei der Verwendung eines Computers zu Fehlfunktionen des Betriebssystems kommen. Das Problem, auf das ich heute gestoßen bin, bestand darin, dass das System beim Zugriff auf gpedit.msc mitteilte, dass das Gruppenrichtlinienobjekt nicht geöffnet werden könne, weil möglicherweise die richtigen Berechtigungen fehlten. Das Gruppenrichtlinienobjekt auf diesem Computer konnte nicht geöffnet werden: 1. Beim Zugriff auf gpedit.msc meldet das System, dass das Gruppenrichtlinienobjekt auf diesem Computer aufgrund fehlender Berechtigungen nicht geöffnet werden kann. Details: Das System kann den angegebenen Pfad nicht finden. 2. Nachdem der Benutzer auf die Schaltfläche „Schließen“ geklickt hat, wird das folgende Fehlerfenster angezeigt. 3. Überprüfen Sie sofort die Protokolleinträge und kombinieren Sie die aufgezeichneten Informationen, um festzustellen, dass das Problem in der Datei C:\Windows\System32\GroupPolicy\Machine\registry.pol liegt
 Was soll ich tun, wenn Steam keine Verbindung zum Remote-Computer herstellen kann?
Mar 01, 2023 pm 02:20 PM
Was soll ich tun, wenn Steam keine Verbindung zum Remote-Computer herstellen kann?
Mar 01, 2023 pm 02:20 PM
Lösung für das Problem, dass Steam keine Verbindung zum Remote-Computer herstellen kann: 1. Klicken Sie in der Spieleplattform auf die Option „Steam“ in der oberen linken Ecke. 2. Öffnen Sie das Menü und wählen Sie die Option „Einstellungen“. Option „Remote Play“; 4. Aktivieren Sie die Funktion „Remote Play“ und klicken Sie auf die Schaltfläche „OK“.
 Python-Skript zum Abmelden vom Computer
Sep 05, 2023 am 08:37 AM
Python-Skript zum Abmelden vom Computer
Sep 05, 2023 am 08:37 AM
Im heutigen digitalen Zeitalter spielt die Automatisierung eine entscheidende Rolle bei der Rationalisierung und Vereinfachung verschiedener Aufgaben. Eine dieser Aufgaben besteht darin, sich vom Computer abzumelden, was normalerweise manuell durch Auswahl der Abmeldeoption auf der Benutzeroberfläche des Betriebssystems erfolgt. Aber was wäre, wenn wir diesen Prozess mithilfe eines Python-Skripts automatisieren könnten? In diesem Blogbeitrag erfahren Sie, wie Sie mit nur wenigen Codezeilen ein Python-Skript erstellen, mit dem Sie sich von Ihrem Computer abmelden können. In diesem Artikel führen wir Sie Schritt für Schritt durch die Erstellung eines Python-Skripts zum Abmelden von Ihrem Computer. Wir behandeln die notwendigen Voraussetzungen, besprechen verschiedene Möglichkeiten zum programmgesteuerten Abmelden und stellen eine Schritt-für-Schritt-Anleitung zum Schreiben des Skripts bereit. Darüber hinaus gehen wir auf plattformspezifische Überlegungen ein und beleuchten Best Practices






