Wie man den Assoziationsregel-Apriori-Algorithmus versteht
Verstehen Sie den Assoziationsregel-Apriori-Algorithmus: Der Apriori-Algorithmus ist der erste Assoziationsregel-Mining-Algorithmus und der klassischste Algorithmus. Er verwendet eine iterative Methode der schichtweisen Suche, um die Beziehung zwischen Elementmengen in der Datenbank zu finden und Regeln zu bilden . Der Prozess besteht aus Verbindungen. Er besteht aus [matrixähnlichen Operationen] und Bereinigung [Entfernen unnötiger Zwischenergebnisse].

Den Assoziationsregel-Apriori-Algorithmus verstehen:
1. Konzept
Tabelle 1 Transaktionsdatenbank eines Supermarkts
Transaktionsnummer TID | Von Kunden gekaufte Artikel | Transaktionsnummer TID |
Vom Kunden gekaufte Artikel |
T1 |
Brot, Sahne, Milch, Tee |
T6 |
Brot , Tee |
|
T2 |
Brot, Sahne, Milch |
T7 |
Bier, Milch, Tee |
T3 |
Kuchen, Milch |
T8 |
Brot, Tee |
T4 |
Milch, Tee |
T9 |
Brot, Sahne, Milch, Tee |
|
T5 |
Brot, Kuchen, Milch |
T10 |
Brot, Milch, Tee |
Definition 1: Sei I={i1,i2,…,im}, was eine Menge von m verschiedenen Projekten ist, und jedes ik wird als Projekt bezeichnet. Eine Sammlung I von Elementen wird als itemset bezeichnet. Die Anzahl seiner Elemente wird als Länge des Itemsets bezeichnet, und ein Itemset mit der Länge k wird als k-Itemset bezeichnet. Im Beispiel ist jedes Produkt ein Artikel, die Artikelmenge ist I={Brot, Bier, Kuchen, Sahne, Milch, Tee} und die Länge von I beträgt 6.
Definition 2: Jede TransaktionT ist eine Teilmenge der Artikelmenge I. Für jede Transaktion gibt es eine eindeutige Identifikationstransaktionsnummer, die als TID aufgezeichnet wird. Alle Transaktionen bilden die TransaktionsdatenbankD, und |D| entspricht der Anzahl der Transaktionen in D. Das Beispiel enthält 10 Transaktionen, also |D|=10.
Definition 3: Für Itemset X setze count(X⊆T) auf die Anzahl der Transaktionen, die support(X)=count(X⊆T)/|D|Im Beispiel erscheint X={Brot, Milch} in T1, T2, T5, T9 und T10, sodass die Unterstützung 0,5 beträgt.
Definition vier:
Minimale Unterstützung ist der minimale Unterstützungsschwellenwert des Itemsets, aufgezeichnet als SUPmin, der die minimale Bedeutung der Zuordnungsregeln darstellt, die den Benutzern wichtig sind. Elementmengen, deren Unterstützung nicht weniger als SUPmin beträgt, werden als häufige Mengen bezeichnet, und häufige Mengen mit der Länge k werden als k-häufige Mengen bezeichnet. Wenn SUPmin auf 0,3 gesetzt ist, beträgt die Unterstützung von {Brot, Milch} im Beispiel 0,5, es handelt sich also um einen 2-häufigen Satz. Definition fünf:
Assoziationsregel ist eine Implikation: R: . Gibt an, dass, wenn der Artikelsatz X in einer bestimmten Transaktion erscheint, auch Y mit einer bestimmten Wahrscheinlichkeit erscheint. Verbandsregeln, die den Benutzern am Herzen liegen, können an zwei Maßstäben gemessen werden: Unterstützung und Glaubwürdigkeit. Definition 6
: Die
Unterstützung
einer AssoziationsregelR ist das Verhältnis der Anzahl der Transaktionen, die der Transaktionssatz sowohl X als auch Y enthält, zu |D|. Das heißt: support(X⇒Y)=count(X⋃Y)/|D|Support spiegelt die Wahrscheinlichkeit wider, dass X und Y gleichzeitig auftreten. Die Unterstützung von Assoziationsregeln entspricht der Unterstützung häufiger Mengen. Definition 7
: Für die Assoziationsregel
R bezieht sichGlaubwürdigkeit
auf das Verhältnis der Anzahl der Transaktionen, die X und Y enthalten, zur Anzahl der Transaktionen, die X enthalten. Das heißt: Konfidenz(X⇒Y)=Unterstützung(X⇒Y)/Unterstützung(X)Konfidenz spiegelt die Wahrscheinlichkeit wider, dass die Transaktion Y enthält, wenn X in der Transaktion enthalten ist. Generell sind für Nutzer nur Vereinsregeln mit hoher Unterstützung und Glaubwürdigkeit von Interesse. Definition 8: Legen Sie die Mindestunterstützung und Mindestglaubwürdigkeit der Verbandsregeln als SUPmin und CONFmin fest. Wenn die Unterstützung und Glaubwürdigkeit der Regel R nicht geringer als SUPmin und CONFmin sind, spricht man von einer „starken Assoziationsregel“. Der Zweck des Association Rule Mining besteht darin, starke Assoziationsregeln zu finden, die den Händlern bei der Entscheidungsfindung helfen.
Diese acht Definitionen umfassen mehrere wichtige Grundkonzepte im Zusammenhang mit Assoziationsregeln. Es gibt zwei Hauptprobleme beim Assoziationsregel-Mining:- Suchen Sie alle häufigen Itemsets in der Transaktionsdatenbank, die größer oder gleich der vom Benutzer angegebenen Mindestunterstützung sind.
- Verwenden Sie häufige Elementsätze, um die erforderlichen Assoziationsregeln zu generieren, und filtern Sie starke Assoziationsregeln basierend auf der vom Benutzer festgelegten Mindestglaubwürdigkeit heraus.
Derzeit untersuchen Forscher hauptsächlich das erste Problem. Es ist schwierig, häufige Mengen zu finden, aber es ist relativ einfach, starke Assoziationsregeln mit häufigen Mengen neu zu generieren.
2. Theoretische Grundlagen
Betrachten wir zunächst die Eigenschaften einer häufigen Menge.
Theorem: Wenn die Elementmenge X eine häufige Menge ist, dann sind ihre nicht leeren Teilmengen alle häufige Mengen .
Nach dem Satz unterscheiden sich bei gegebener Itemmenge Dies beweist, dass die k-Kandidatenmenge, die durch die Verkettung von k-1 häufigen Mengen erzeugt wird, die k-häufige Menge abdeckt. Wenn gleichzeitig die Itemmenge Y in der k-Kandidatenmenge eine k-1-Ordnungsteilmenge enthält, die nicht zur k-1-häufigen Menge gehört, kann Y keine häufige Menge sein und sollte aus der Kandidatenmenge entfernt werden. Der Apriori-Algorithmus macht sich diese Eigenschaft häufiger Mengen zunutze.
3. Algorithmusschritte:
Zuerst sind die Testdaten:
Transaktions-ID | Produkt-ID Liste T100 I 3 |
| T400 | I1, I2, I4 |
| T500 | I1, I3 |
| T600 | I2, I3 |
| T700 | I1, I3 |
|
T800 |
I1,I2,I3,I5 |
| T90 0 | I1,I2,I3 |
Das obige ist der detaillierte Inhalt vonWie man den Assoziationsregel-Apriori-Algorithmus versteht. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1385
1385
 52
52
 Wie löste ich das Problem der Berechtigungen beim Betrachten der Python -Version in Linux Terminal?
Apr 01, 2025 pm 05:09 PM
Wie löste ich das Problem der Berechtigungen beim Betrachten der Python -Version in Linux Terminal?
Apr 01, 2025 pm 05:09 PM
Lösung für Erlaubnisprobleme beim Betrachten der Python -Version in Linux Terminal Wenn Sie versuchen, die Python -Version in Linux Terminal anzuzeigen, geben Sie Python ein ...
 Wie kann ich die gesamte Spalte eines Datenrahmens effizient in einen anderen Datenrahmen mit verschiedenen Strukturen in Python kopieren?
Apr 01, 2025 pm 11:15 PM
Wie kann ich die gesamte Spalte eines Datenrahmens effizient in einen anderen Datenrahmen mit verschiedenen Strukturen in Python kopieren?
Apr 01, 2025 pm 11:15 PM
Bei der Verwendung von Pythons Pandas -Bibliothek ist das Kopieren von ganzen Spalten zwischen zwei Datenrahmen mit unterschiedlichen Strukturen ein häufiges Problem. Angenommen, wir haben zwei Daten ...
 Wie lehre ich innerhalb von 10 Stunden die Grundlagen für Computer-Anfänger-Programmierbasis in Projekt- und problemorientierten Methoden?
Apr 02, 2025 am 07:18 AM
Wie lehre ich innerhalb von 10 Stunden die Grundlagen für Computer-Anfänger-Programmierbasis in Projekt- und problemorientierten Methoden?
Apr 02, 2025 am 07:18 AM
Wie lehre ich innerhalb von 10 Stunden die Grundlagen für Computer -Anfänger für Programmierungen? Wenn Sie nur 10 Stunden Zeit haben, um Computer -Anfänger zu unterrichten, was Sie mit Programmierkenntnissen unterrichten möchten, was würden Sie dann beibringen ...
 Wie kann man vom Browser vermeiden, wenn man überall Fiddler für das Lesen des Menschen in der Mitte verwendet?
Apr 02, 2025 am 07:15 AM
Wie kann man vom Browser vermeiden, wenn man überall Fiddler für das Lesen des Menschen in der Mitte verwendet?
Apr 02, 2025 am 07:15 AM
Wie kann man nicht erkannt werden, wenn Sie Fiddlereverywhere für Man-in-the-Middle-Lesungen verwenden, wenn Sie FiddLereverywhere verwenden ...
 Was sind reguläre Ausdrücke?
Mar 20, 2025 pm 06:25 PM
Was sind reguläre Ausdrücke?
Mar 20, 2025 pm 06:25 PM
Regelmäßige Ausdrücke sind leistungsstarke Tools für Musteranpassung und Textmanipulation in der Programmierung, wodurch die Effizienz bei der Textverarbeitung in verschiedenen Anwendungen verbessert wird.
 Wie hört Uvicorn kontinuierlich auf HTTP -Anfragen ohne Serving_forver () an?
Apr 01, 2025 pm 10:51 PM
Wie hört Uvicorn kontinuierlich auf HTTP -Anfragen ohne Serving_forver () an?
Apr 01, 2025 pm 10:51 PM
Wie hört Uvicorn kontinuierlich auf HTTP -Anfragen an? Uvicorn ist ein leichter Webserver, der auf ASGI basiert. Eine seiner Kernfunktionen ist es, auf HTTP -Anfragen zu hören und weiterzumachen ...
 Was sind einige beliebte Python -Bibliotheken und ihre Verwendung?
Mar 21, 2025 pm 06:46 PM
Was sind einige beliebte Python -Bibliotheken und ihre Verwendung?
Mar 21, 2025 pm 06:46 PM
In dem Artikel werden beliebte Python-Bibliotheken wie Numpy, Pandas, Matplotlib, Scikit-Learn, TensorFlow, Django, Flask und Anfragen erörtert, die ihre Verwendung in wissenschaftlichen Computing, Datenanalyse, Visualisierung, maschinellem Lernen, Webentwicklung und h beschreiben
 Wie erstelle ich dynamisch ein Objekt über eine Zeichenfolge und rufe seine Methoden in Python auf?
Apr 01, 2025 pm 11:18 PM
Wie erstelle ich dynamisch ein Objekt über eine Zeichenfolge und rufe seine Methoden in Python auf?
Apr 01, 2025 pm 11:18 PM
Wie erstellt in Python ein Objekt dynamisch über eine Zeichenfolge und ruft seine Methoden auf? Dies ist eine häufige Programmieranforderung, insbesondere wenn sie konfiguriert oder ausgeführt werden muss ...




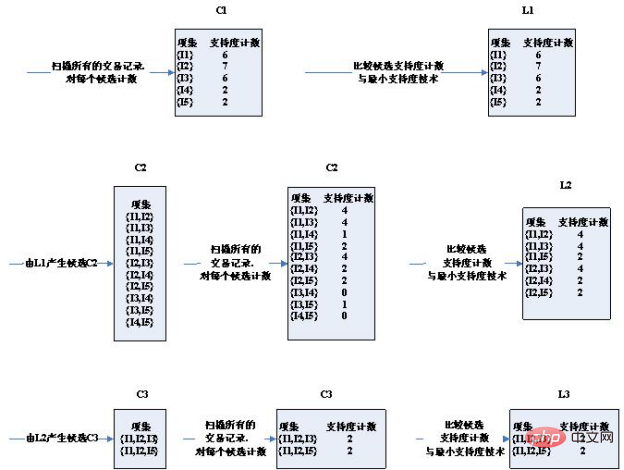 Es ist zu erkennen, dass der Kandidatensatz in der dritten Runde deutlich reduziert wurde.
Es ist zu erkennen, dass der Kandidatensatz in der dritten Runde deutlich reduziert wurde. 