

In diesem Artikel lernen wir die Logik hinter Merge Sort kennen und implementieren sie in JavaScript. Abschließend wird die Zusammenführungssortierung hinsichtlich der räumlichen und zeitlichen Komplexität mit anderen Algorithmen verglichen.
Die Zusammenführungssortierung verwendet das Konzept von Teilen und Erobern, um eine bestimmte Liste von Elementen zu sortieren. Dabei wird das Problem in kleinere Teilprobleme zerlegt, bis diese einfach genug sind, um direkt gelöst zu werden.
Das Folgende sind die Schritte der Zusammenführungssortierung:
1. Teilen Sie die gegebene Liste in zwei Hälften (wenn die Anzahl der Elemente in der Liste ungerade ist, machen Sie sie ungefähr gleich).
2. Teilen Sie die Unterarrays auf die gleiche Weise weiter, bis nur noch ein einziges Elementarray übrig bleibt.
3. Beginnen Sie mit einem einzelnen Elementarray und führen Sie Unterarrays zusammen, um jedes zusammengeführte Unterarray zu sortieren. 4. Wiederholen Sie Schritt 3, bis Sie endlich ein sortiertes Array erhalten.
Am Beispiel des Arrays [4, 8, 7, 2, 11, 1, 3] sehen wir uns an, wie die Zusammenführungssortierung funktioniert:
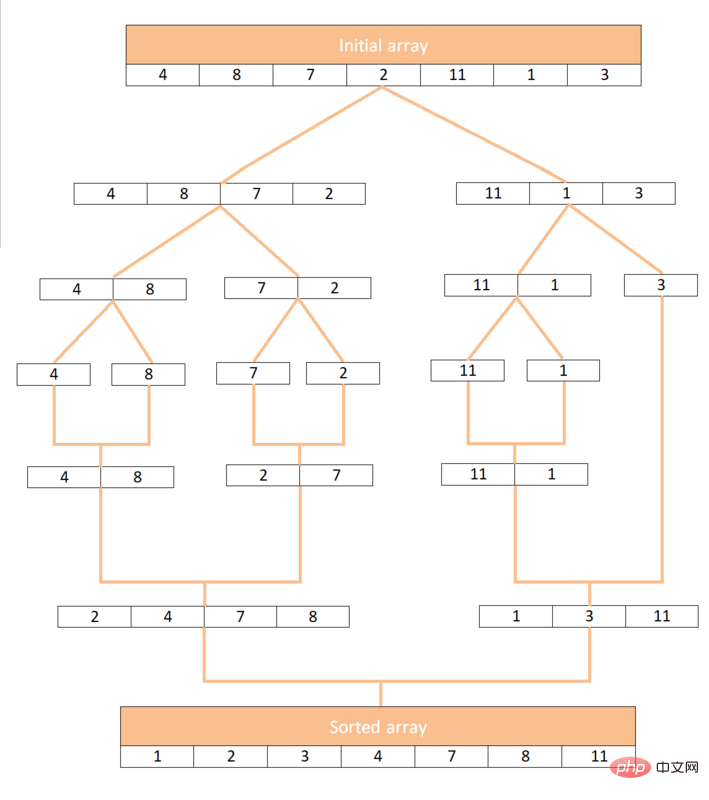
[4, 8, 7, 2, 11, 1, 3] 为例,让我们看一下归并排序是如何工作的:

首先实现一个将两个已排序子数组合并为一个已排序数组的函数 merge() 。要注意着两个子数组是已经被排好序的,这一点非常重要, merge() 函数只用于其进行合并。【推荐教程:《JavaScript视频教程》】
可以通过遍历这两个子数组来实现:
function merge(left, right) {
let arr = []
// 如果任何一个数组为空,就退出循环
while (left.length && right.length) {
// 从左右子数组的最小元素中选择较小的元素
if (left[0] < right[0]) {
arr.push(left.shift())
} else {
arr.push(right.shift())
}
}
// 连接剩余的元素,防止没有把两个数组遍历完整
return [ ...arr, ...left, ...right ]
}在这个函数中,通过把两个排好序的子数组(left、right)合并来获得一个排好序的大数组。首先,创建一个空数组。之后在 left 和 right 两个子数组中最小元素中的较小的一个,并将其添加到空数组。我们只需要检查 left 和 right 子数组中的第一个元素,因为它们是已排好序的。
在这个过程中,从子数组中删除了被选择的元素(通过 shift() 函数实现)。继续这个过程,直到其中一个子数组变为空。最后把非空子数组的剩余元素(因为它们已经被排序)插入主数组的最后面。
现在有了合并两个已排序数组的代码,接下来为实现归并排序算法的最终代码。这意味着要继续分割数组,直到最终只包含一个元素的数组为止:
function mergeSort(array) {
const half = array.length / 2
if(array.length < 2){
return array
}
const left = array.splice(0, half)
return merge(mergeSort(left),mergeSort(array))
}在代码中先确定中点,并用 splice() 函数将数组分为两个子数组。如果元素数量为奇数,则左侧的元素数量会少一个。不断的划分数组,直到剩下单个元素的数组(array.length < 2)。然后用之前实现的 merge()
merge(), der zwei sortierte Unterarrays zu einem sortierten Array zusammenführt. Es ist wichtig zu beachten, dass die beiden Subarrays bereits sortiert sind und die Funktion merge() nur zum Zusammenführen verwendet wird. [Empfohlenes Tutorial: „JavaScript-Video-Tutorial"]
array = [4, 8, 7, 2, 11, 1, 3]; console.log(mergeSort(array));
In dieser Funktion wird ein großes sortiertes Array durch Zusammenführen zweier sortierter Unterarrays (links, rechts) erhalten. Erstellen Sie zunächst ein leeres Array. Nehmen Sie dann das kleinere der kleinsten Elemente in den beiden Unterarrays left und right und fügen Sie es dem leeren Array hinzu. Wir müssen nur das erste Element in den Subarrays left und right überprüfen, da diese bereits sortiert sind.
Bei diesem Vorgang wird das ausgewählte Element aus dem Subarray gelöscht (implementiert durch die Funktion shift()). Setzen Sie diesen Vorgang fort, bis eines der Subarrays leer ist. Fügen Sie abschließend die verbleibenden Elemente des nicht leeren Unterarrays (da sie sortiert wurden) am Ende des Hauptarrays ein. Da wir nun den Code zum Zusammenführen zweier sortierter Arrays haben, ist hier der endgültige Code zum Implementieren des Sortieralgorithmus zum Zusammenführen. Das bedeutet, dass Sie das Array weiter aufteilen, bis Sie am Ende ein Array haben, das nur ein Element enthält:
1,2,3,4,7,8,11
Bestimmen Sie im Code zunächst den Mittelpunkt und verwenden Sie die Funktion splice(), um das Array in zwei Unterarrays aufzuteilen . Wenn die Anzahl der Elemente ungerade ist, ist die Anzahl der Elemente auf der linken Seite um eins geringer. Teilen Sie das Array kontinuierlich, bis ein Array aus einzelnen Elementen übrig bleibt (array.length ). Führen Sie dann die Subarrays mit der zuvor implementierten Funktion <code>merge() zusammen.
Die Ausgabe entspricht den Erwartungen:
rrreeeEffizienz der ZusammenführungssortierungDie schlechteste Zeitkomplexität der Zusammenführungssortierung ist $O(n\log n)$, was dem schnellen Sortieren entspricht. Die optimale Fallzeitkomplexität ist dieselbe. Merge Sort ist einer der schnellsten derzeit verfügbaren Sortieralgorithmen.
🎜Im Gegensatz zur Schnellsortierung ist die Zusammenführungssortierung kein 🎜In-Place-Sortieralgorithmus, was bedeutet, dass sie zusätzlich zum Eingabearray zusätzlichen Platz beansprucht. Dies liegt daran, dass wir ein Hilfsarray zum Speichern von Unterarrays verwenden. Die räumliche Komplexität der Zusammenführungssortierung beträgt $O(n)$. 🎜🎜Ein weiterer Vorteil der Zusammenführungssortierung besteht darin, dass sie sich sehr gut für Multithreading eignet, da jede geteilte Hälfte unabhängig sortiert werden kann. Eine weitere übliche Möglichkeit, die Laufzeit der Zusammenführungssortierung zu verkürzen, besteht darin, die Einfügungssortierung zu verwenden, wenn Sie ein relativ kleines Subarray (ca. 7 Elemente) erreichen. Dies liegt daran, dass die Einfügungssortierung sehr gut mit kleinen oder nahezu sortierten Arrays funktioniert. 🎜🎜Zusammenfassung🎜🎜In diesem Artikel haben wir die Logik hinter dem Merge-Sort-Algorithmus kennengelernt und ihn in JavaScript implementiert. Es ist einer der grundlegenden Sortieralgorithmen und kann uns helfen, die Divide-and-Conquer-Strategie besser zu verstehen. 🎜🎜Weitere Kenntnisse zum Thema Programmierung finden Sie unter: 🎜Videokurse zum Programmieren🎜! ! 🎜Das obige ist der detaillierte Inhalt vonJavaScript-Algorithmus-Merge-Sortier-Algorithmus (ausführliche Erklärung). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!