Warum werden negative Zahlen in Computern im Zweierkomplement gespeichert?
Die Verwendung des Zweierkomplementspeichers für negative Zahlen in Computern kann die grundlegenden Rechenschaltungen des Computers vereinfachen, sodass Addition und Subtraktion nur mit Additionsschaltungen implementiert werden müssen und Addition anstelle von Subtraktion verwendet wird. Das Komplement ist der kleinste positive kongruente Rest einer negativen Zahl, sodass das Addieren einer negativen Zahl und das Subtrahieren einer positiven Zahl beide durch Addieren eines Komplements dargestellt werden können.

Die Betriebsumgebung dieses Tutorials: Windows 7-System, Dell G3-Computer.
1. Einführung
Wissen Sie, wie ganze Zahlen in Computern gespeichert werden? Ist es das Vorzeichenbit plus das Wertbit? Werden die Wertbits im normalen Binärformat gespeichert?
Wenn Sie die letzten beiden Fragen mit „Ja“ beantworten, bedeutet dies, dass bei der Speicherung im 3-Bit-Binärformat und dem Vorzeichenbit 0 für positiv und 1 für negativ steht, 1 als 001, -1 gespeichert wird Es wird als 101 gespeichert. Leider ist dies nicht der Fall. Computer speichern ganze Zahlen in der Form eines Zweierkomplements statt in der natürlich aussehenden Form. Obwohl das Zweierkomplement auch durch das Vorzeichenbit plus das Wertbit dargestellt wird, sind die Ausdrucksregeln unterschiedlich: 1 wird als 001 gespeichert, -1 wird als 111 gespeichert. 001,-1会存储成101。可惜事实不是这样,计算机中是用补码的形式而不是刚刚那种看上去很自然的形式存储整数,补码虽然也是用符号位加值位来表示,但表示的规则不太一样:1会存成001,-1会存成111。
如果三个问题你都回答对了,你知道计算机中整数以补码的形式存储,但你知道为什么要用这种形式吗?以及「正数的补码等于原码;负数的补码等于反码加1,而反码等于原码符号位不变,其余各位取反」这样的补码到底意味着什么?(假设你不知道,请接着往下看吧 XD)
先看使用补码的目的,然后忘掉上面那个补码定义,跟我从这个目的开始,一步步探索补码的本质。
目的:为了简化计算机基本运算电路,使加减法都只需要通过加法电路实现,也就是让减去一个正数或加上一个负数这样的运算可以用加上一个正数来代替。于是改变负数存储的形式,存储成一种可以直接当成正数来相加的形式,这种形式就是补码。(正数不用变,所以接下来的讨论中一般略去正数)
2.补码是怎么把减法变成加法的?
2.1.用时钟理解减法变加法
这是一个身边的例子,当你校对时钟的时候,假设发现钟是6点,但实际上现在才2点,也就是它走快了4个小时,你可以有两种方法进行校正,一种是逆时针拨回4个小时到2点,另一种是顺时针拨6个小时到12点然后再拨2小时,也就是顺时针拨8个小时到2点。所以对于时钟的表盘来说,设-N表示逆时针拨N个小时,N表示顺时针拨动N个小时,那么-4 = +8,同样还会有 -1 = +11、-5 = +7,甚至也可以 -4 = +8 = +20 = +32 = -16...
这里边隐藏了什么规律?其实在数学中,-4、+8、+20、+32、-16可以归为符合某个条件的同一类数字 —— 对于模12同余。
中文维基上对于模和同余的定义是:两个整数a、b,若它们除以正整数m所得的余数相等,则称a、b对于模m同余。
而在一个可溢出计数系统中,把计数系统容量作为模,那么所有对此模同余的数在此计数系统中都会有同样的表示,而且运算等价。
比如上面例子中的时钟表盘就是一个可溢出计数系统,模为12,所以-4、+8、+20、+32、-16这些对模12同余的数在时钟表盘上的表示是一样的,而且对时针做这些操作的结果也是一样的,都会拨到同样的位置。
一个n位二进制构成的计数系统,因为会舍弃溢出的高位,所以也是一个可溢出的计数系统,它的模为(2^n) 。(从0数到(2^n -1),再多就溢出)
由此可以推理,在一个3位二进制构成的模为8的计数系统中,-2,-10,6,14
Wenn Sie alle drei Fragen richtig beantwortet haben, wissen Sie, dass ganze Zahlen in Computern im Zweierkomplementformat gespeichert werden, aber wissen Sie, warum dieses Format verwendet wird? Und
"Das Komplement einer positiven Zahl ist gleich dem Originalcode; das Komplement einer negativen Zahl ist gleich dem Komplement plus 1, und das Komplement ist gleich dem Vorzeichenbit des Originalcodes, und die übrigen Bits sind unverändert invertiert.“Was bedeutet eine solche Ergänzung? (Wenn Sie es nicht wissen, lesen Sie bitte weiter.) Lassen Sie uns zunächst den Zweck der Verwendung von Komplementcodes betrachten und dann die obige Definition von Komplementcodes vergessen. Folgen Sie mir ausgehend von diesem Zweck und die Komplementierung Schritt für Schritt erforschen.
Zweck: Um die grundlegende Computeroperationsschaltung zu vereinfachen, müssen Addition und Subtraktion nur über die Additionsschaltung implementiert werden, d. h. es können eine positive Zahl subtrahiert oder eine negative Zahl addiert werden durch
2 Wie wandelt der Komplementcode die Subtraktion in die Addition um?
2.1. Verwenden Sie die Uhr, um die Subtraktion und Addition um 2 Uhr zu verstehen. Das heißt, sie geht 4 Stunden schneller. Sie können sie auf zwei Arten korrigieren. Die andere besteht darin, sie 6 Stunden im Uhrzeigersinn auf 12 Uhr zu drehen und dann weitere 2 Stunden zu wählen, d. h. 8 Stunden im Uhrzeigersinn auf 2 Uhr zu drehen. Wenn also für das Zifferblatt der Uhr-N das Drehen um N Stunden gegen den Uhrzeigersinn und N das Drehen um N Stunden im Uhrzeigersinn bedeutet, dann ist -4 = +8 , es wird auch -1 = +11, -5 = +7 und sogar -4 = +8 = + 20 = +32 = -16 geben ...Welche Regeln verbergen sich hier? Tatsächlich können
-4, +8, +20, +32, -16in der Mathematik als Zahlen desselben Typs klassifiziert werden, die bestimmte Bedingungen erfüllen –für Kongruenz Modulo 12
. 🎜🎜Die Definition von Modul und Kongruenz im chinesischen Wiki lautet: zwei ganze Zahlen a und b, wenn die Reste, die man durch Division durch eine positive ganze Zahl m erhält, gleich sind, dann sagt man a und b kongruent modulo m sein. 🎜🎜
Wenn in einem überlaufbaren Zählsystem die Kapazität des Zählsystems als Modulo verwendet wird, dann haben alle Zahlen, die mit diesem Modul kongruent sind, in diesem Zählsystem die gleiche Darstellung, und die Operationen werden gleichwertig sein.
Beispielsweise ist das Zifferblatt im obigen Beispiel ein Überlaufzählsystem, Modulo 12, sodass-4, +8, +20, +32, -16mit Modulo 12 kongruent sind Die auf dem Zifferblatt der Uhr angezeigten Zahlen sind dieselben, und auch die Ergebnisse dieser Vorgänge am Stundenzeiger sind dieselben, sie werden alle auf dieselbe Position eingestellt. 🎜Ein Zählsystem, das aus n-Bit-Binärdateien besteht. Da die übergelaufenen hohen Bits verworfen werden, ist es auch ein überlauffähiges Zählsystem und sein Modul beträgt (2^n). (Zählen von 0 bis (2^n -1), alle anderen werden überlaufen)
Daraus kann geschlossen werden, dass in einem 3-Bit-Binärzählsystem Modulo 8,-2, -10 , 6, 14kann durch dieselbe Binärzahl dargestellt werden. Wenn Sie 10 subtrahieren und gleichzeitig 14 addieren, erhalten Sie das gleiche Ergebnis. 🎜🎜🎜🎜2.2. Führe zum Komplementcode🎜🎜🎜🎜Solange der Komplementcode der positive kongruente Rest einer negativen Zahl ist, können wir den gleichen Effekt erzielen wie dieser positive kongruente Komplementcode Hinzufügen einer weiteren negativen Zahl🎜. Für eine negative Zahl gibt es unzählige positive Kongruenzen, die die Bedingungen erfüllen. Um unnötige Operationen zu reduzieren, kann angegeben werden, dass das Komplement die kleinste positive Zahl unter ihnen ist. 🎜🎜Vielleicht wird es Komplementcode genannt, weil das Finden des Komplementcodes über den Originalcode eine komplementäre Modulo-Operation ist. 🎜🎜🎜Beachten Sie, dass die Komplementcodes hier alle speziell von mir markiert sind, da dies nicht die tatsächliche Komplementform ist, die im Computer gespeichert ist. Sie sollte Komplementnummer heißen, aber glauben Sie mir, sie kommt sehr nahe
3. Perfektionieren Sie den Komplementcode
3.1 Es gibt immer noch einige Probleme mit dieser Komplementcode-Darstellung
Durch die Konvertierung in den Komplementcode wird das Subtrahieren einer Zahl sehr gut Aber es gibt ein offensichtliches Problem: Das Symbol der Zahl selbst geht verloren.
Beispielsweise stellt eine dreistellige Binärzahl normalerweise 0~7 dar. Mit der Komplementmethode kann sie die Operation von -8~-1 ersetzen, aber nicht wirklich - 8~-1, weil Sie nicht wissen, ob es sich um eine positive oder negative Zahl handelt. 0~7,使用补码法它能代替-8~-1的运算,但它不能真正表示-8~-1,因为你不知道它到底是正数还是负数。
我们把负数转换成了一种在运算中更让计算机喜欢的形式,但它却丢失了自己本身作为数的信息。
怎么解决这个问题,可能有人很快就拍脑袋:那就加一位来表示正负得了。但这样的话运算时怎么办,从第二位开始算么?那进位去位的时候是不是也需要特别注意一下不要影响到符号位?你会发现这个问题并不是那么简单。
3.2.怎么完善 补码
不知道大牛是怎么想到的,问题解决得非常完美:
- 在保持补码特性的前提下 (也就是减一个数还是照样变成加一个数)
- 增加正负的表示 (能真正表示
-8~-1Wir haben negative Zahlen in eine Form umgewandelt, die für Computer in Berechnungen angenehmer ist, aber sie haben die Informationen über sich selbst als Zahl verloren. - 3.2. Wie man den Komplementcode verbessert
Wie löst man dieses Problem? Manche Leute schlagen sich vielleicht schnell den Kopf: Fügen Sie dann eine Ziffer hinzu, um positiv oder negativ anzuzeigen. Aber was soll ich in diesem Fall bei der Berechnung tun? Soll ich ab der zweiten Ziffer beginnen? Müssen wir bei der Ausführung von Bits besonders darauf achten, dass das Vorzeichenbit nicht beeinträchtigt wird? Sie werden feststellen, dass das Problem nicht so einfach ist.
Ich weiß nicht, wie Daniel darauf gekommen ist, aber das Problem wurde perfekt gelöst:
-8 wirklich ausdrücken). ~-1, Schauen Sie sich einfach an, ob das Vorzeichenbit 0 oder 1 ist) Und die Lösung ist wirklich dumm, überraschend einfach, so ist es an den Sie zuvor gedacht haben:
Fügen Sie eine Ziffer hinzu, um positiv und negativ darzustellen.
Die spezifische Methode ist: Fügen Sie dem oberen Bit auf der linken Seite ein Vorzeichenbit hinzu, zusammen mit dem Pseudo-Komplementcode, den wir zuvor abgeleitet haben, bildet es einen wirklich perfekten
Komplementcode- .
- Erzielter Effekt: Durch Lesen des Vorzeichenbits können Sie das Vorzeichen der Zahl ermitteln. Gleichzeitig ist das Vorzeichenbit wie das Wertbit an der Additionsoperation an der Operation beteiligt.
- 4. Zum Schluss
- Zusammenfassen
Das obige ist der detaillierte Inhalt vonWarum werden negative Zahlen in Computern im Zweierkomplement gespeichert?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1382
1382
 52
52
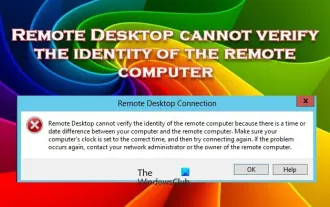 Remotedesktop kann die Identität des Remotecomputers nicht authentifizieren
Feb 29, 2024 pm 12:30 PM
Remotedesktop kann die Identität des Remotecomputers nicht authentifizieren
Feb 29, 2024 pm 12:30 PM
Mit dem Windows-Remotedesktopdienst können Benutzer aus der Ferne auf Computer zugreifen, was für Personen, die aus der Ferne arbeiten müssen, sehr praktisch ist. Es können jedoch Probleme auftreten, wenn Benutzer keine Verbindung zum Remotecomputer herstellen können oder Remotedesktop die Identität des Computers nicht authentifizieren kann. Dies kann durch Netzwerkverbindungsprobleme oder einen Fehler bei der Zertifikatsüberprüfung verursacht werden. In diesem Fall muss der Benutzer möglicherweise die Netzwerkverbindung überprüfen, sicherstellen, dass der Remote-Computer online ist, und versuchen, die Verbindung wiederherzustellen. Außerdem ist es wichtig, sicherzustellen, dass die Authentifizierungsoptionen des Remotecomputers richtig konfiguriert sind, um das Problem zu lösen. Solche Probleme mit den Windows-Remotedesktopdiensten können normalerweise durch sorgfältiges Überprüfen und Anpassen der Einstellungen behoben werden. Aufgrund eines Zeit- oder Datumsunterschieds kann Remote Desktop die Identität des Remotecomputers nicht überprüfen. Bitte stellen Sie Ihre Berechnungen sicher
 Die CSRankings National Computer Science Rankings 2024 sind veröffentlicht! CMU dominiert die Liste, MIT fällt aus den Top 5
Mar 25, 2024 pm 06:01 PM
Die CSRankings National Computer Science Rankings 2024 sind veröffentlicht! CMU dominiert die Liste, MIT fällt aus den Top 5
Mar 25, 2024 pm 06:01 PM
Die 2024CSRankings National Computer Science Major Rankings wurden gerade veröffentlicht! In diesem Jahr gehört die Carnegie Mellon University (CMU) im Ranking der besten CS-Universitäten in den Vereinigten Staaten zu den Besten des Landes und im Bereich CS, während die University of Illinois at Urbana-Champaign (UIUC) einen der besten Plätze belegt sechs Jahre in Folge den zweiten Platz belegt. Georgia Tech belegte den dritten Platz. Dann teilten sich die Stanford University, die University of California in San Diego, die University of Michigan und die University of Washington den vierten Platz weltweit. Es ist erwähnenswert, dass das Ranking des MIT zurückgegangen ist und aus den Top 5 herausgefallen ist. CSRankings ist ein globales Hochschulrankingprojekt im Bereich Informatik, das von Professor Emery Berger von der School of Computer and Information Sciences der University of Massachusetts Amherst initiiert wurde. Die Rangfolge erfolgt objektiv
 Was ist e im Computer?
Aug 31, 2023 am 09:36 AM
Was ist e im Computer?
Aug 31, 2023 am 09:36 AM
Das „e“ von Computer ist das Symbol der wissenschaftlichen Notation. Der Buchstabe „e“ wird als Exponententrennzeichen in der wissenschaftlichen Notation verwendet, was „multipliziert mit der Zehnerpotenz“ bedeutet. In der wissenschaftlichen Notation wird eine Zahl normalerweise als M × geschrieben 10^E, wobei M eine Zahl zwischen 1 und 10 ist und E den Exponenten darstellt.
 Fix: Microsoft Teams-Fehlercode 80090016 Das Trusted Platform-Modul Ihres Computers ist ausgefallen
Apr 19, 2023 pm 09:28 PM
Fix: Microsoft Teams-Fehlercode 80090016 Das Trusted Platform-Modul Ihres Computers ist ausgefallen
Apr 19, 2023 pm 09:28 PM
<p>MSTeams ist die vertrauenswürdige Plattform zum Kommunizieren, Chatten oder Telefonieren mit Teamkollegen und Kollegen. Der Fehlercode 80090016 auf MSTeams und die Meldung <strong>Das Trusted Platform Module Ihres Computers ist fehlgeschlagen</strong> kann zu Schwierigkeiten beim Anmelden führen. Die App erlaubt Ihnen keine Anmeldung, bis der Fehlercode behoben ist. Wenn Sie beim Öffnen von MS Teams oder einer anderen Microsoft-Anwendung auf solche Meldungen stoßen, kann Ihnen dieser Artikel bei der Lösung des Problems helfen. </p><h2&
 Was bedeutet Computer-Cu?
Aug 15, 2023 am 09:58 AM
Was bedeutet Computer-Cu?
Aug 15, 2023 am 09:58 AM
Die Bedeutung von cu in einem Computer hängt vom Kontext ab: 1. Steuereinheit, im Zentralprozessor eines Computers, CU ist die Komponente, die für die Koordinierung und Steuerung des gesamten Rechenprozesses verantwortlich ist. 2. Recheneinheit, in einem Grafikprozessor oder einem anderen Beschleunigter Prozessor, CU ist die Grundeinheit zur Verarbeitung paralleler Rechenaufgaben.
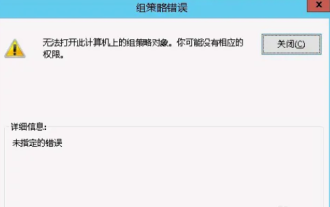 Das Gruppenrichtlinienobjekt kann auf diesem Computer nicht geöffnet werden
Feb 07, 2024 pm 02:00 PM
Das Gruppenrichtlinienobjekt kann auf diesem Computer nicht geöffnet werden
Feb 07, 2024 pm 02:00 PM
Gelegentlich kann es bei der Verwendung eines Computers zu Fehlfunktionen des Betriebssystems kommen. Das Problem, auf das ich heute gestoßen bin, bestand darin, dass das System beim Zugriff auf gpedit.msc mitteilte, dass das Gruppenrichtlinienobjekt nicht geöffnet werden könne, weil möglicherweise die richtigen Berechtigungen fehlten. Das Gruppenrichtlinienobjekt auf diesem Computer konnte nicht geöffnet werden: 1. Beim Zugriff auf gpedit.msc meldet das System, dass das Gruppenrichtlinienobjekt auf diesem Computer aufgrund fehlender Berechtigungen nicht geöffnet werden kann. Details: Das System kann den angegebenen Pfad nicht finden. 2. Nachdem der Benutzer auf die Schaltfläche „Schließen“ geklickt hat, wird das folgende Fehlerfenster angezeigt. 3. Überprüfen Sie sofort die Protokolleinträge und kombinieren Sie die aufgezeichneten Informationen, um festzustellen, dass das Problem in der Datei C:\Windows\System32\GroupPolicy\Machine\registry.pol liegt
 Was ist Komplementcode?
Aug 09, 2023 pm 05:20 PM
Was ist Komplementcode?
Aug 09, 2023 pm 05:20 PM
Das Einerkomplement ist eine Zahlendarstellung, die üblicherweise für die binäre Zahlenarithmetik in Computern verwendet wird. Der Komplementcode vereinfacht die Additions- und Subtraktionsoperationen negativer Zahlen und kann einen größeren Bereich ganzer Zahlen darstellen. Die Verwendung des Komplementcodes spielt eine wichtige Rolle in der Informatik und ist sehr wichtig für das Verständnis der Operation und Darstellung ganzer Zahlen in Computern.
 Was soll ich tun, wenn Steam keine Verbindung zum Remote-Computer herstellen kann?
Mar 01, 2023 pm 02:20 PM
Was soll ich tun, wenn Steam keine Verbindung zum Remote-Computer herstellen kann?
Mar 01, 2023 pm 02:20 PM
Lösung für das Problem, dass Steam keine Verbindung zum Remote-Computer herstellen kann: 1. Klicken Sie in der Spieleplattform auf die Option „Steam“ in der oberen linken Ecke. 2. Öffnen Sie das Menü und wählen Sie die Option „Einstellungen“. Option „Remote Play“; 4. Aktivieren Sie die Funktion „Remote Play“ und klicken Sie auf die Schaltfläche „OK“.



