 häufiges Problem
häufiges Problem
 Wie hoch ist die zeitliche Komplexität eines Programms, das den binären Suchalgorithmus verwendet?
Wie hoch ist die zeitliche Komplexität eines Programms, das den binären Suchalgorithmus verwendet?
Wie hoch ist die zeitliche Komplexität eines Programms, das den binären Suchalgorithmus verwendet?
Die zeitliche Komplexität eines Programms, das den binären Suchalgorithmus verwendet, liegt auf der „logarithmischen Ebene“. Die binäre Suche ist eine hocheffiziente Suchmethode. Die Komplexität des Algorithmus ist die Anzahl der While-Schleifen. Die Zeitkomplexität kann als „O(h)=O(log2n)“ ausgedrückt werden.

Die Betriebsumgebung dieses Tutorials: Windows 7-System, Dell G3-Computer.
Die zeitliche Komplexität eines Programms, das den binären Suchalgorithmus verwendet, liegt auf der „logarithmischen Ebene“.
Verwandte Empfehlungen: „Programmieren lernen“
Die binäre Suche wird auch als binäre Suche (Binary Search) bezeichnet und ist eine effizientere Suchmethode. Die binäre Suche erfordert jedoch, dass die lineare Tabelle eine sequentielle Speicherstruktur annimmt und die Elemente in der Tabelle nach Schlüsselwörtern geordnet werden müssen.
Suchvorgang:
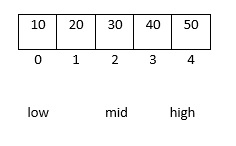
Angenommen, die Elemente in der Tabelle sind in aufsteigender Reihenfolge angeordnet, vergleichen Sie die in der Mitte der Tabelle aufgezeichneten Schlüsselwörter mit den Suchschlüsselwörtern. Wenn die beiden gleich sind, ist die Suche erfolgreich. Andernfalls verwenden Sie die Datensätze in der Mitte, um die Tabelle zu verschieben. Sie ist in zwei Untertabellen unterteilt, die vordere und die hintere. Wenn das in der mittleren Position aufgezeichnete Schlüsselwort größer als das Suchschlüsselwort ist, wird die vorherige Untertabelle durchsucht weiter, andernfalls wird die letztgenannte Untertabelle weiter durchsucht. Wiederholen Sie den obigen Vorgang, bis ein Datensatz gefunden wird, der die Bedingungen erfüllt, wodurch die Suche erfolgreich ist, oder bis die Untertabelle nicht mehr vorhanden ist. In diesem Fall schlägt die Suche fehl.
Algorithmuskomplexität:
Die Grundidee der binären Suche besteht darin, n Elemente in zwei ungefähr gleiche Teile zu teilen und a[n/2] mit x zu vergleichen Wenn x gefunden wird, wird der Algorithmus beendet, wenn .
Die Zeitkomplexität die Anzahl der While-Schleifen ist.
Es gibt insgesamt n Elemente,
folgt nach und nach n, n/2, n/4, .... n/2^k (die verbleibende Anzahl der Elemente, die als nächstes bearbeitet werden sollen), wobei k die Zahl ist von Schleifen
Da Ihr n/2^k gerundet ist >=1
Das heißt, wenn n/2^k=1
, können Sie k=log2n erhalten (was der Logarithmus von n zur Basis 2 ist)
so die Zeit Die Komplexität kann ausgedrückt werden als O(h)=O(log2n)
Das Folgende ist ein Pseudocode für die Implementierung der binären Suche:
BinarySearch(max,min,des) mid-<(max+min)/2 while(min<=max) mid=(min+max)/2 if mid=des then return mid elseif mid >des then max=mid-1 else min=mid+1 return max
Die Halbsuchmethode wird auch als binäre Suchmethode bezeichnet. Sie nutzt die Ordnungsbeziehung zwischen Elementen vollständig aus und übernimmt die Divide-and-Conquer-Strategie. Im schlimmsten Fall kann die Suchaufgabe in O(log n) abgeschlossen werden. Seine Grundidee ist: (unter der Annahme, dass die Array-Elemente in aufsteigender Reihenfolge angeordnet sind) n Elemente in zwei Hälften mit ungefähr der gleichen Anzahl teilen, a[n/2] nehmen und es mit dem x vergleichen, das Sie finden möchten, wenn x= a[n/ 2] dann wird x gefunden und der Algorithmus endet; wenn x Weitere verwandte Artikel finden Sie auf der Chinesischen PHP-Website! ! Das obige ist der detaillierte Inhalt vonWie hoch ist die zeitliche Komplexität eines Programms, das den binären Suchalgorithmus verwendet?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 So schreiben Sie einen binären Suchalgorithmus mit C#
Sep 19, 2023 pm 12:42 PM
So schreiben Sie einen binären Suchalgorithmus mit C#
Sep 19, 2023 pm 12:42 PM
So schreiben Sie mit C# einen binären Suchalgorithmus. Er findet die Position eines bestimmten Elements in einem geordneten Array mit einer Zeitkomplexität von O(logN). In C# können wir mit den folgenden Schritten einen binären Suchalgorithmus schreiben. Schritt 1: Daten vorbereiten Zuerst müssen wir ein sortiertes Array als Zieldaten für die Suche vorbereiten. Angenommen, wir möchten die Position eines bestimmten Elements in einem Array ermitteln. int[]data={1,3,5,7,9,11,13
 Java-Programm zum Finden der Kubikwurzel einer Zahl mithilfe eines binären Suchalgorithmus
Aug 28, 2023 pm 01:33 PM
Java-Programm zum Finden der Kubikwurzel einer Zahl mithilfe eines binären Suchalgorithmus
Aug 28, 2023 pm 01:33 PM
Eine Kubikwurzel ist ein ganzzahliger Wert, der dreimal hintereinander mit sich selbst multipliziert den ursprünglichen Wert ergibt. In diesem Artikel schreiben wir ein Java-Programm, das die binäre Suche verwendet, um die Kubikwurzel einer Zahl zu finden. Das Finden der Kubikwurzel einer Zahl ist eine Anwendung des binären Suchalgorithmus. In diesem Artikel besprechen wir ausführlich, wie man die binäre Suche zur Berechnung von Kubikwurzeln verwendet. Eingabe-Ausgabe-Beispiel Beispiel 1: Eingabe: 64 Ausgabe: 4 Die Kubikwurzel von 64 ist beispielsweise 4 und die Ausgabe ist 4. Beispiel 2: Eingabe: 216 Ausgabe: 6 Beispielsweise ist die Kubikwurzel von 216 6 und die Ausgabe ist 6. Binäre Suche Die binäre Suche ist ein Algorithmus zum Suchen von Elementen (d. h. Schlüsseln in einem sortierten Array). Binärer Algorithmus funktioniert
 In C-Sprache geschriebenes binäres Suchprogramm, das pthread für die Multithread-Verarbeitung verwendet
Aug 26, 2023 pm 12:45 PM
In C-Sprache geschriebenes binäres Suchprogramm, das pthread für die Multithread-Verarbeitung verwendet
Aug 26, 2023 pm 12:45 PM
Wir wissen, dass die binäre Suchmethode der am besten geeignete und effektivste Sortieralgorithmus ist. Dieser Algorithmus funktioniert mit sortierten Sequenzen. Der Algorithmus ist einfach: Er findet einfach das Element in der Mitte, teilt dann die Liste in zwei Teile und bewegt sich zur linken oder rechten Unterliste. Wir kennen seinen Algorithmus. Jetzt werden wir sehen, wie man die binäre Suchtechnik in einer Multithread-Umgebung verwendet. Die Anzahl der Threads hängt von der Anzahl der im System vorhandenen Kerne ab. Werfen wir einen Blick auf den Code, um eine Vorstellung davon zu bekommen. Beispiel#include<iostream>#defineMAX16#defineMAX_THREAD4usingnamespacestd;//placearr,keyandothervariabl
 Wie finde ich das kleinste Element in einem Array mithilfe des binären Suchalgorithmus in C-Sprache?
Aug 25, 2023 pm 08:37 PM
Wie finde ich das kleinste Element in einem Array mithilfe des binären Suchalgorithmus in C-Sprache?
Aug 25, 2023 pm 08:37 PM
Die Programmiersprache C bietet zwei Suchtechniken. Sie lauten wie folgt: Lineare Suche Binäre Suche Binäre Suche Diese Methode eignet sich nur für geordnete Listen. Die angegebene Liste ist in zwei gleiche Teile unterteilt. Das angegebene Schlüsselwort wird mit dem mittleren Element der Liste verglichen. Hier können drei Dinge passieren: Wenn das mittlere Element mit dem Schlüsselwort übereinstimmt, wird die Suche hier erfolgreich beendet. Wenn das mittlere Element größer als das Schlüsselwort ist, findet die Suche in der linken Partition statt. Wenn das mittlere Element kleiner als das Schlüsselwort ist, wird die Suche in der rechten Partition durchgeführt. Eingabe (i/p) – unsortierte Liste von Elementen, Schlüsselwörtern. Ausgabe (o/p)-success-if failed to find the keyword-otherwise key=20mid=(low+high)/2 Programm 1 Das Folgende ist die Verwendung der binären Suche in
 Wie implementiert man einen binären Suchalgorithmus mit Python?
Sep 20, 2023 pm 01:24 PM
Wie implementiert man einen binären Suchalgorithmus mit Python?
Sep 20, 2023 pm 01:24 PM
Wie implementiert man einen binären Suchalgorithmus mit Python? Der binäre Suchalgorithmus, auch binärer Suchalgorithmus genannt, ist ein effizienter Suchalgorithmus. Es funktioniert bei geordneten Arrays oder Listen und grenzt die Suche ein, indem der Zielwert mit Elementen in der Mitte des Arrays verglichen wird. Im Folgenden wird die Implementierung des binären Suchalgorithmus in Python vorgestellt und spezifische Codebeispiele bereitgestellt. Algorithmusidee: Vergleichen Sie den Zielwert mit dem Element in der Mitte des Arrays. Wenn sie gleich sind, geben Sie die Elementposition zurück, wenn der Zielwert größer ist als das Element in der Mitte
 So implementieren Sie einen binären Suchalgorithmus mit Java
Sep 19, 2023 pm 12:57 PM
So implementieren Sie einen binären Suchalgorithmus mit Java
Sep 19, 2023 pm 12:57 PM
So implementieren Sie einen binären Suchalgorithmus mit Java. Der binäre Suchalgorithmus ist eine effiziente Suchmethode, die für sortierte Arrays geeignet ist. Seine Grundidee besteht darin, den Suchbereich kontinuierlich einzuschränken, den Suchwert mit den Elementen in der Mitte des Arrays zu vergleichen und basierend auf dem Vergleichsergebnis zu entscheiden, ob die Suche in der linken oder rechten Hälfte fortgesetzt werden soll, bis das Zielelement gefunden wird oder Der Suchbereich wird auf leer reduziert. Im Folgenden stellen wir detailliert vor, wie der binäre Suchalgorithmus in Java implementiert wird. Schritt 1: Implementieren Sie die binäre Suchmethode publicclassBinarySearch
 Verwenden Sie in einem C-Programm den binären Suchalgorithmus, um rationale Zahlen zu suchen, ohne Gleitkomma-Arithmetik zu verwenden
Aug 27, 2023 pm 06:05 PM
Verwenden Sie in einem C-Programm den binären Suchalgorithmus, um rationale Zahlen zu suchen, ohne Gleitkomma-Arithmetik zu verwenden
Aug 27, 2023 pm 06:05 PM
In diesem Problem erhalten wir eine sortierte Reihe rationaler Zahlen. Wir müssen einen binären Suchalgorithmus verwenden, um nach einem bestimmten Element dieses Arrays rationaler Zahlen zu suchen, ohne Gleitkommaoperationen zu verwenden. Rationale Zahlen sind Zahlen, die in der Form p/q ausgedrückt werden, wobei p und q beide ganze Zahlen sind. Zum Beispiel ⅔, ⅕. Die binäre Suche ist eine Suchtechnik, die Elemente findet, indem sie in der Mitte eines Arrays sucht. Wird verwendet, um Elemente in einem sortierten Array rationaler Zahlen mithilfe der binären Suche zu finden, wobei Gleitkommaoperationen nicht zulässig sind. Wir vergleichen Zähler und Nenner, um herauszufinden, welches Element größer ist bzw. welches Element dasjenige ist, das gefunden werden soll. Beispiel: Erstellen wir hierfür ein Programm, #include<stdio.h>structRational{ &am
 Analyse des PHP-Algorithmus: Wie verwende ich den binären Suchalgorithmus, um Elemente in einem geordneten Array schnell zu finden?
Sep 19, 2023 pm 01:14 PM
Analyse des PHP-Algorithmus: Wie verwende ich den binären Suchalgorithmus, um Elemente in einem geordneten Array schnell zu finden?
Sep 19, 2023 pm 01:14 PM
Analyse des PHP-Algorithmus: Wie verwende ich den binären Suchalgorithmus, um Elemente in einem geordneten Array schnell zu finden? Übersicht: Der binäre Suchalgorithmus ist ein effizienter Suchalgorithmus, der zum Auffinden bestimmter Elemente in einem geordneten Array geeignet ist. In diesem Artikel wird das Prinzip des binären Suchalgorithmus ausführlich vorgestellt und PHP-Codebeispiele gegeben. Prinzip: Der binäre Suchalgorithmus findet das Zielelement schnell, indem er den Suchbereich wiederholt um die Hälfte reduziert. Der Vorgang ist wie folgt: Grenzen Sie zunächst den Suchbereich auf den Anfang und das Ende des Arrays ein. Berechnen Sie dann den Index des mittleren Elements und vergleichen Sie ihn mit dem Zielelement.




