
Python löst fortgeschrittene Mathematikprobleme und meine Mutter muss sich nicht mehr um mein Studium kümmern

Verwenden Sie Python, um Probleme wie Grenzwerte, Ableitungen, partielle Ableitungen, bestimmte Integrale, unbestimmte Integrale, Doppelintegrale usw. zu lösen . in fortgeschrittener Mathematik
1.3 Taylor-Erweiterungsformelreihe1.4 Symbolische ErweiterungSympy ist eine Python-Bibliothek für wissenschaftliches Rechnen, die darauf abzielt, ein voll ausgestattetes Computeralgebrasystem zu sein. SymPy umfasst Funktionen von der grundlegenden symbolischen Arithmetik bis hin zu Analysis, Algebra, diskreter Mathematik und Quantenphysik. Es kann die Ergebnisse in LaTeX anzeigen.网Offizielle Website von Sympy Erweitern
2. Finden Sie den Grenzwert
from sympy import *import sympy
x = Symbol("x")y = Symbol("y")sympy.I
sympy.E
sympy.oo
sympy.pi
sympy.root(8,3)
sympy.log(1024,2)
 Finde den Fakultät
Finde den Fakultätsympy.factorial(4)Nach dem Login kopierenTrigonometrische Funktionen
sympy.sin(sympy.pi)sympy.tan(sympy.pi/4)sympy.cos(sympy.pi/2)
1.2 Ausdruck erweitern
f = (1+x)**3expand(f)
x 3 + 3 x 2 + 3 x + 1 \displaystyle x^{3} + 3 x^{2} + 3 x + 1 x3+3x2+3x+1
1.3 泰勒展开公式series
ln(1+x).series(x,0,4)
x
−
x
2
2
+
x
3
3
+
O
(
x
4
)
\displaystyle x - \frac{x^{2}}{2} + \frac{x^{3}}{3} + O\left(x^{4}Rechts)
2 x 2 + 3x 3 +O (x 4)
x
−
x
3
6
+
x
5
120
−
x
7
5040
+
O
(
x
8
)
\displaystyle x - \frac{x^{3}}{6} + \frac{x^{5}}{120} - \frac{x^{7}}{5040} + O\left(x^{8}Rechts)
6 x 3 + 120x 5 − 504 0x7 +O(x 8)
1
−
x
2
2
+
x
4
24
−
x
6
720
+
x
8
40320
+
O
(
x
9
)
\displaystyle 1 - \frac{x^{2}}{2} + \frac{x^{4}}{24} - \frac{x^{6}}{720} + \frac{x^{8}}{40320} + O\left(x^{9}Rechts)
1 x 2 + 24x 4 − 720 x6 +40320 x 8 +O (x9 )
1
−
x
+
x
2
−
x
3
+
x
4
+
O
(
x
5
)
\displaystyle 1 - x + x^{2} - x^{3} + x^{4} + O\left(x^{5}Rechts)
1−x+ x2 −x 3+ x4+ O( x5)
x
+
x
3
3
+
O
(
x
4
)
\displaystyle x + \frac{x^{3}}{3} + O\left(x^{4}\right)
x+3x3+O(x4)
1
+
x
+
x
2
+
x
3
+
O
(
x
4
)
\displaystyle 1 + x + x^{2} + x^{3} + O\left(x^{4}\right)
1+x+x2+x3+O(x4)
1
−
x
+
x
2
−
x
3
+
O
(
x
4
)
\displaystyle 1 - x + x^{2} - x^{3} + O\left(x^{4}\right)
1−x+x2−x3+O(x4) 1.4 符号展开
x
a
+
b
\displaystyle x^{a + b}
xa+b 2. 求极限limit
1
\displaystyle 1
1
(
x
+
1
)
1
x
\displaystyle \left(x + 1\right)^{\frac{1}{x}}
(x+1)x1 重要极限 dir可以表示极限的趋近方向
e
1
x
+
1
\displaystyle e^{\frac{1}{x}} + 1
ex1+1
1
\displaystyle 1
1
∞
\displaystyle \infty
∞ 3. 求导diff diff(函数,自变量,求导次数) 3.1 一元函数 求导问题
2
cos
(
2
x
)
\displaystyle 2 \cos{\left(2 x \right)}
2cos(2x)
1
x
\displaystyle \frac{1}{x}
x1 3.2 多元函数 求偏导问题
−
x
y
sin
(
x
y
)
+
cos
(
x
y
)
\displaystyle - x y \sin{\left(x y \right)} + \cos{\left(x y \right)}
−xysin(xy)+cos(xy) 4. 积分integrate 4.1 定积分
−
1.54366666666667
\displaystyle -1.54366666666667
−1.54366666666667
1
\displaystyle 1
1 4.2 不定积分
atan
(
x
)
\displaystyle \operatorname{atan}{\left(x \right)}
atan(x) 4.3 双重积分
11.6666666666667
\displaystyle 11.6666666666667
11.6666666666667 5. 求解方程组solve {x: -1, y: 4} 6. 计算求和式summation 计算求和式可以使用sympy.summation函数,其函数原型为sympy.summation(f, *symbols, **kwargs) 10100 到这里就结束了,如果对你有帮助,欢迎点赞关注评论,你的点赞对我很重要。在此也祝愿大家可以把数学学好 相关免费学习推荐:python教程(视频)sin(x).series(x,0,8)
cos(x).series(x,0,9)
(1/(1+x)).series(x,0,5)
tan(x).series(x,0,4)
(1/(1-x)).series(x,0,4)
(1/(1+x)).series(x,0,4)
a = Symbol("a")b = Symbol("b")#simplify( )普通的化简simplify((x**3 + x**2 - x - 1)/(x**2 + 2*x + 1))#trigsimp( )三角化简trigsimp(sin(x)/cos(x))#powsimp( )指数化简powsimp(x**a*x**b)limit(sin(x)/x,x,0)
f2=(1+x)**(1/x)
f2
f1=sin(x)/x
f2=(1+x)**(1/x)f3=(1+1/x)**x
lim1=limit(f1,x,0)lim2=limit(f2,x,0)lim3=limit(f3,x,oo)print(lim1,lim2,lim3)
1 E E
f4 = (1+exp(1/x))f4
lim4 = limit(f4,x,0,dir="-")lim4
lim5 = limit(f4,x,0,dir="+")lim5
diff(sin(2*x),x)
diff(ln(x),x)
diff(sin(x*y),x,y)
f = x**2 + 1integrate(f,(x,-1.1))
integrate(exp(x),(x,-oo,0))
f = 1/(1+x*x)integrate(f,x)
f = (4/3)*x + 2*y
integrate(f,(x,0,1),(y,-3,4))
#解方程组#定义变量f1=x+y-3f2=x-y+5solve([f1,f2],[x,y])
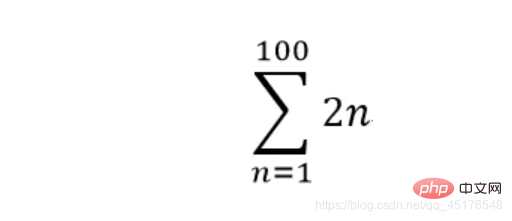
**sympy.summation(2 * n,(n,1,100))
Das obige ist der detaillierte Inhalt vonLernen Sie Python, um fortgeschrittene Mathematikprobleme zu lösen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!