Die Speicherstruktur von Diagrammen
Das Konzept der Diagramme ist fast eingeführt. Sie können es verdauen und den folgenden Inhalt weiter lernen. Wenn es keine Probleme gibt, werden wir den nächsten Inhalt weiter studieren. Dies ist natürlich nicht der problematischste Teil, da wir heute lediglich die Speicherstruktur des Diagramms vorstellen.
Sequentielle Speicherstruktur von Diagrammen: Adjazenzmatrix
Was ist eine Adjazenzmatrix?
Schauen wir uns zunächst an, wie eine sequentielle Struktur zum Speichern von Diagrammen verwendet wird. Unabhängig davon, ob es sich um einen Stapel, eine Warteschlange oder einen Baum handelt, können wir ein einfaches Array verwenden, um die sequentielle Speicherfähigkeit dieser Datenstrukturen zu erreichen. Aber der Graph ist anders. Aus dem vorherigen Artikel haben wir gelernt, dass die Darstellung eines Knotens die Form
[Empfehlung: PHP-Video-Tutorial]
In der Graphenterminologie wird die sequentielle Speicherstruktur eines Graphen, der durch ein zweidimensionales Array dargestellt wird, als Adjazenzmatrix bezeichnet. Genau wie das Formular unten.
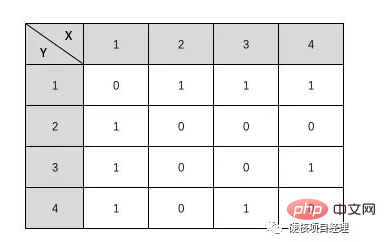
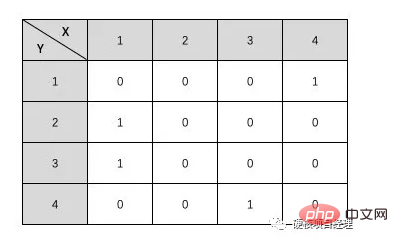
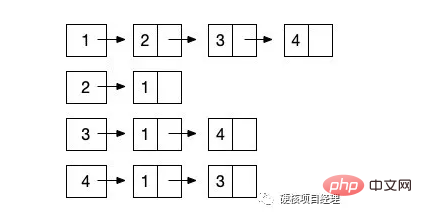
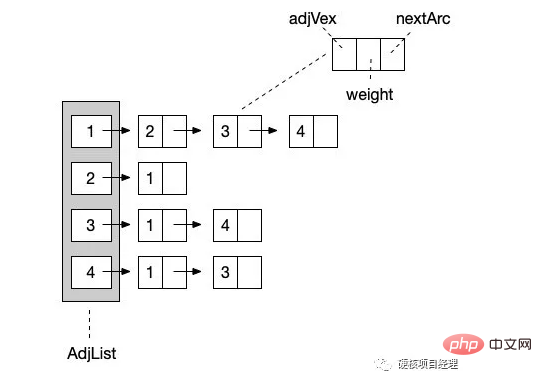
In dieser Tabelle haben wir zwei horizontale und vertikale Koordinaten, ob es eine Kante zwischen einem Knoten gibt. Beispielsweise hat das Koordinatenpaar X1 und Y2 Wie sieht das Diagramm aus, das der obigen Adjazenzmatrix entspricht? Sie können versuchen, es selbst zu zeichnen. Es macht nichts, wenn Sie es nicht zeichnen können, denn wir haben gerade erst mit dem Lernen begonnen. Tatsächlich handelt es sich um die Adjazenzmatrix des Graphen, den wir zuerst gezeigt haben. Das Bild links entspricht der Adjazenzmatrix in der Tabelle oben. Wie sieht also die Adjazenzmatrix des gerichteten Graphen rechts aus? Versuchen wir es auch mit dem Schreiben. Interessant, oder? Was also, wenn es sich um eine mächtige Handlung handelt? Tatsächlich ist es sehr einfach, die 1 im Diagramm durch das Gewicht der entsprechenden Kante zu ersetzen. Es ist jedoch möglich, dass das Gewicht einiger Kanten 0 ist, sodass wir in einem gewichteten Diagramm eine sehr definieren können große ZahlOder definieren Sie eine sehr kleine negative Zahl als unendliche Zahl, um anzuzeigen, dass diese beiden Knoten keine Kanten haben. Aufbau der Adjazenzmatrix Als nächstes werden wir die Speicherstruktur einer solchen Adjazenzmatrix durch Code konstruieren. Zur Implementierung verwenden wir immer noch das Beispiel eines ungerichteten Graphen. Da ein ungerichteter Graph erfordert, dass dem umgekehrten Knoten ein Wert zugewiesen wird, hat er einen Schritt mehr als ein gerichteter Graph, und die anderen sind grundsätzlich ähnlich. In diesem Code initialisieren wir zunächst eine zweidimensionale Matrix über die Methode CreateGraph(). Das heißt, basierend auf der Anzahl der von uns eingegebenen Knoten wird eine zweidimensionale Array-Struktur von X * Y implementiert und alle ihre Werte werden als 0 definiert. Mit anderen Worten, dieser Graph hat derzeit keine Kanten. Nachdem die BuildGraph()-Methode CreateGraph() aufruft, fahren wir mit der Eingabe der Kanteninformationen fort. Geben Sie zunächst die Anzahl der Kanten ein. Wenn die Anzahl der Kanten kleiner oder gleich 0 ist, erstellen Sie diese nicht weiter. Tatsächlich können wir strenger sein und sicherstellen, dass die Kanten die maximale Grenze basierend auf den Definitionen von ungerichteten vollständigen Graphen und gerichteten vollständigen Graphen nicht überschreiten können. Als nächstes geben wir weiterhin Kanteninformationen in einer Schleife ein. Das Eingabeformat, das ich hier benötige, ist der ausgehende Knoten, der eingehende Knoten und die Gewichtung. Da es sich bei unserem Beispiel um einen ungerichteten Graphen handelt, müssen wir zusätzlich zum Erstellen von Kanten für Die Erklärung des Codes kann immer noch recht abstrakt sein. Führen Sie es einfach aus und probieren Sie es aus. Rufen Sie unsere PHP-Datei in der Befehlszeilenumgebung auf und geben Sie dann die relevanten Informationen der Reihe nach entsprechend den Eingabeaufforderungen ein. Ist der Inhalt des endgültig gedruckten Arrays genau derselbe wie in unserer Tabelle oben? Mit einem einfachen Code realisieren wir die sequentielle Speicherung von Diagrammen. 可能有的同学会一时懵圈。因为我第一眼看到的时候也是完全懵了，不过仔细的对比画出来的图和上面的表格其实马上就能想明白了。这次我们真的是进入二维的世界了。是不是感觉图瞬间就把树甩到十万八千里之外了。完全二叉树的时候，我们的思想是二维的，但结构还是一维的，而到邻接矩阵的时候，不管是思想还是代码结构，全部都进化到了二维空间，高大上真不是吹的。 图的链式存储结构：邻接表 说完顺序存储结构，自然不能忽视另一种形式的存储结构，那就是图的链式存储结构。其实对于图来说，链式结构非常简单和清晰，因为我们只需要知道一个结点和那些结点有边就行了。那么我们就让这个结点形成一个单链表，一路往后链接就好了，就像下图这样。（同样以上图无向图为例） 从 结点1 开始，它指向一个后继是 结点2 ，然后继续向后链接 结点3 和 结点4 。这样，与 结点1 相关的边就都描述完成了。由于我们展示的依然是无向图的邻接表表示，所以 结点2 的链表结点指向了 结点 1 。也就是完成了 对于代码实现来说，我们可以将头结点，也就是正式的 1-4 结点保存在一个顺序表中。然后让每个数组元素的值为第一个结点的内容。这样，我们就可以让链表结点只保存结点名称、权重和下一个结点对象的指向信息就可以了。 接下来，我们来看看如何使用邻接表这种结构来建立图。 代码中的注释已经写得很清楚了。可以看出，在邻接表的操作中，无向图也是一样的比有向图多一步操作的，如果只是建立有向图的话，可以不需要 p2 结点的操作。特别需要注意的就是，在这段代码中，我们使用的是链表操作中的 头插法 。也就是最后一条数据会插入到 头结点 上，而最早的那个边会在链表的最后。大家看一下最后建立完成的数据结构的输出就明白了。 使用邻接表来建立的图的链式存储结构是不是反而比邻接矩阵更加的清晰明了一些。就像树的链式和顺序结构一样，在图中它们的优缺点也是类似的。邻接矩阵占用的物理空间更多，因为它需要两层一样多元素的数组，就像上面的表格一样，需要占据 4 * 4 的物理格子。而邻接表我们可以直接数它的结点数，只需要 12 个格子就完成了。而且，更主要的是，链式的邻接表可以随时扩展边结点和边数，不需要重新地初始化，我们只需要简单地修改上面的测试代码就能够实现，而邻接矩阵如果要修改结点数的话，就得要重新初始化整个二维数组了。 总结 对于图来说，除了邻接矩阵和邻接表之外，还有其它的一些存储形式，不过都是链式的邻接表的一些优化和变形而已。大家有兴趣的可以自己去了解一下 十字链表 、邻接多重表 这两种存储结构。 好了，基础的存储结构已经铺垫完了，关于图的概念也都熟悉掌握了，接下来，我们就要准备去做最重要的操作了，那就是如何来对图进行遍历。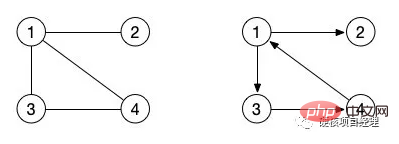
// 邻接矩阵
$graphArr = [];
function CreateGraph($Nv, &$graphArr)
{
$graphArr = [];
for ($i = 1; $i <= $Nv; $i++) {
for ($j = 1; $j <= $Nv; $j++) {
$graphArr[$i][$j] = 0;
}
}
}
// 邻接矩阵
function BuildGraph(&$graphArr)
{
echo '请输入结点数：';
fscanf(STDIN, "%d", $Nv);
CreateGraph($Nv, $graphArr);
if ($graphArr) {
echo '请输入边数：';
fscanf(STDIN, "%d", $Ne);
if ($Ne > 0) {
for ($i = 1; $i <= $Ne; $i++) {
echo '请输入边，格式为 出 入 权：';
fscanf(STDIN, "%d %d %d", $v1, $v2, $weight);
$graphArr[$v1][$v2] = $weight;
// 如果是无向图，还需要插入逆向的边
$graphArr[$v2][$v1] = $weight;
}
}
}
}BuildGraph($graphArr);
// 请输入结点数：4
// 请输入边数：4
// 请输入边，格式为 出 入 权：1 2 1
// 请输入边，格式为 出 入 权：1 3 1
// 请输入边，格式为 出 入 权：1 4 1
// 请输入边，格式为 出 入 权：3 4 1
print_r($graphArr);
// Array
// (
// [1] => Array
// (
// [1] => 0
// [2] => 1
// [3] => 1
// [4] => 1
// )
// [2] => Array
// (
// [1] => 1
// [2] => 0
// [3] => 0
// [4] => 0
// )
// [3] => Array
// (
// [1] => 1
// [2] => 0
// [3] => 0
// [4] => 1
// )
// [4] => Array
// (
// [1] => 1
// [2] => 0
// [3] => 1
// [4] => 0
// )
// )
// x
//y 0 1 1 1
// 1 0 0 0
// 1 0 0 1
// 1 0 1 0
// 头结点
class AdjList
{
public $adjList = []; // 顶点列表
public $Nv = 0; // 结点数
public $Ne = 0; // 边数
}
// 边结点
class ArcNode
{
public $adjVex = 0; // 结点
public $nextArc = null; // 链接指向
public $weight = 0; // 权重
}
function BuildLinkGraph()
{
fscanf(STDIN, "请输入 结点数 边数：%d %d", $Nv, $Ne);
if ($Nv > 1) {
// 初始化头结点
$adj = new AdjList();
$adj->Nv = $Nv; // 保存下来方便使用
$adj->Ne = $Ne; // 保存下来方便使用
// 头结点列表
for ($i = 1; $i <= $Nv; $i++) {
$adj->adjList[$i] = null; // 全部置为 NULL ，一个无边空图
}
if ($Ne > 0) {
//
for ($i = 1; $i <= $Ne; $i++) {
echo '请输入边，格式为 出 入 权：';
fscanf(STDIN, "%d %d %d", $v1, $v2, $weight);
// 建立一个结点
$p1 = new ArcNode;
$p1->adjVex = $v2; // 结点名称为 入结点
$p1->nextArc = $adj->adjList[$v1]; // 下一跳指向 出结点 的头结点
$p1->weight = $weight; // 设置权重
$adj->adjList[$v1] = $p1; // 让头结点的值等于当前新创建的这个结点
// 无向图需要下面的操作，也就是反向的链表也要建立
$p2 = new ArcNode;
// 注意下面两行与上面代码的区别
$p2->adjVex = $v1; // 这里是入结点
$p2->nextArc = $adj->adjList[$v2]; // 这里是出结点
$p2->weight = $weight;
$adj->adjList[$v2] = $p2;
}
return $adj;
}
}
return null;
}print_r(BuildLinkGraph());
// AdjList Object
// (
// [adjList] => Array
// (
// [1] => ArcNode Object
// (
// [adjVex] => 4
// [nextArc] => ArcNode Object
// (
// [adjVex] => 3
// [nextArc] => ArcNode Object
// (
// [adjVex] => 2
// [nextArc] =>
// [weight] => 1
// )
// [weight] => 1
// )
// [weight] => 1
// )
// [2] => ArcNode Object
// (
// [adjVex] => 1
// [nextArc] =>
// [weight] => 1
// )
// [3] => ArcNode Object
// (
// [adjVex] => 4
// [nextArc] => ArcNode Object
// (
// [adjVex] => 1
// [nextArc] =>
// [weight] => 1
// )
// [weight] => 1
// )
// [4] => ArcNode Object
// (
// [adjVex] => 3
// [nextArc] => ArcNode Object
// (
// [adjVex] => 1
// [nextArc] =>
// [weight] => 1
// )
// [weight] => 1
// )
// )
// [Nv] => 4
// [Ne] => 4
// )
测试代码：
https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/5.图/source/5.2图的存储结构.php
Das obige ist der detaillierte Inhalt vonPHP-Datenstruktur-Graph-Speicherstruktur. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
So öffnen Sie eine PHP-Datei
So entfernen Sie die ersten paar Elemente eines Arrays in PHP
Was tun, wenn die PHP-Deserialisierung fehlschlägt?
So verbinden Sie PHP mit der MSSQL-Datenbank
So verbinden Sie PHP mit der MSSQL-Datenbank
So laden Sie HTML hoch
So lösen Sie verstümmelte Zeichen in PHP
So öffnen Sie PHP-Dateien auf einem Mobiltelefon
![[Web-Frontend] Node.js-Schnellstart](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
