Anwendung von Diagrammen: kürzester Weg
Haben Sie das Gefühl, dass Sie im vorherigen Artikel noch mehr über den minimalen Spannbaum lernen müssen? Ich weiß nicht, wie gut es jeder beherrscht. Haben Sie die Prinzipien von Prim und Kruskal verstanden? Wenn Sie es während des Interviews nicht aufschreiben können, geben Sie zumindest eine allgemeine Vorstellung davon. Wenn Sie ein Student sind, der die Aufnahmeprüfung für das Aufbaustudium ablegt, müssen Sie den Code des gesamten Algorithmus genau verstehen und sich daran erinnern.
Was ist der kürzeste Weg?
Heute lernen wir etwas über ein weiteres klassisches Problem in Diagrammanwendungen, nämlich das Problem des kürzesten Pfades. Dieses Problem unterscheidet sich vom minimalen Spannbaum. Die Anforderung des minimalen Spannbaums besteht darin, alle Knoten zu verbinden und die Route mit dem geringsten Gewicht zu nehmen. Der kürzeste Weg bezieht sich auf den Weg mit dem geringsten Gewicht von einem Scheitelpunkt zu einem anderen Scheitelpunkt. Dieser Pfad ist nicht unbedingt im minimalen Spanning Tree enthalten, daher besteht keine große Beziehung zwischen ihnen.
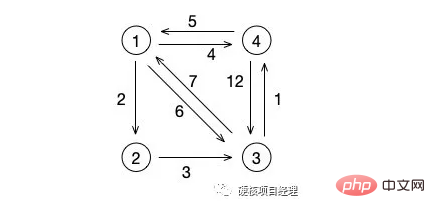
Auf diesem Bild ist unser kürzester Weg von Knoten 1 zu Knoten 2 2, das ist offensichtlich. Was ist also mit Knoten 1 bis Knoten 3? Nicht der direkte Mittelpfad mit einer Gewichtung von 6, sondern der Pfad 1->2->3, also der Pfad mit einer Gesamtgewichtung von 5.
Dann schauen wir uns Knoten 3 an. Der kürzeste Weg von dort zu Knoten 1 sollte der Pfad 3->4->1 sein, also der Pfad mit einer Gewichtung von 6, nicht der mittlere mit einem Gewicht von 7.
Ja, das ist das Konzept des kürzesten Weges. Normalerweise lösen wir das Problem des Einwegdiagramms auf dem kürzesten Weg, aber wie sieht es im wirklichen Leben aus? Die typischsten kartenbezogenen Anwendungen sind eigentlich bidirektionale Diagramme. Dies hat jedoch keinen Einfluss auf unser Lernen. Wir können die Knoten in diesem Beispieldiagramm als Stadtbahnhöfe betrachten. Selbst die Bahnlinien, die Knoten 1 und Knoten 3 verbinden, kommen und gehen nicht unbedingt gleichzeitig. Beispielsweise beträgt die Gesamtfahrzeit des Zuges Z2 von Changsha nach Peking 14 Stunden und 42 Minuten, während die Rückfahrtzeit des Zuges Z1 14 Stunden und 10 Minuten beträgt. Können wir also andere Züge wählen? Es gibt zum Beispiel einen Zug, der von Changsha nach Shijiazhuang nur 8 Stunden und von Shijiazhuang nach Peking nur 2 Stunden braucht. Auf diese Weise beträgt die Gesamtzeit, die wir für diese Route wählen, nur 10 Stunden (natürlich ist dies nur ein Beispiel. Die Leute werden definitiv den Zug am Startbahnhof wählen, wenn es kein Hochgeschwindigkeitszug ist.)
Multi-Source-Shortest-Path-Floyd-Algorithmus
Lassen Sie uns zunächst über einen Multi-Source-Shortest-Path-Algorithmus sprechen. Was ist also Multi-Source?
Tatsächlich kann dieser Algorithmus den kürzesten Weg von allen Knoten zu allen Knoten finden. Das ist richtig, mit diesem Algorithmus wird der kürzeste Weg zwischen ihnen sofort berechnet, egal welcher Knoten zu welchem Knoten geht. Ist es magisch? Nein, nein, nein, was noch erstaunlicher ist und Sie gleich zum Schreien bringen wird, ist der Kerncode, der nur aus fünf Zeilen besteht! !
function Floyd($graphArr){
$n = count($graphArr);
for($k = 1;$k<=$n;$k++){ // 设 k 为经过的结点
for($i = 1;$i<=$n;$i++){
for($j = 1;$j<=$n;$j++){
// 如果经过 k 结点 能使 i 到 j 的路径变短，那么将 i 到 j 之间的更新为通过 k 中转之后的结果
if($graphArr[$i][$j] > $graphArr[$i][$k] + $graphArr[$k][$j]){
$graphArr[$i][$j] = $graphArr[$i][$k] + $graphArr[$k][$j];
}
}
}
}
for($i = 1;$i<=$n;$i++){
for($j = 1;$j<=$n;$j++){
echo $graphArr[$i][$j], ' ';
}
echo PHP_EOL;
}
}
// 请输入结点数：4
// 请输入边数：8
// 请输入边，格式为 出 入 权：1 2 2
// 请输入边，格式为 出 入 权：1 3 6
// 请输入边，格式为 出 入 权：1 4 4
// 请输入边，格式为 出 入 权：2 3 3
// 请输入边，格式为 出 入 权：3 1 7
// 请输入边，格式为 出 入 权：3 4 1
// 请输入边，格式为 出 入 权：4 1 5
// 请输入边，格式为 出 入 权：4 3 12
// 0 2 5 4
// 9 0 3 4
// 6 8 0 1
// 5 7 10 0Nach dem Login kopieren
Wir können zuerst das Ergebnis überprüfen, bei dem es sich um die Matrixausgabe am Ende des Kommentars handelt. Die kürzesten Entfernungen von Knoten 1 zu den Knoten 2, 3 und 4 betragen 2, 5 und 4. Die kürzesten Entfernungen von Knoten 3 zu den Knoten 1, 2 und 4 betragen 6, 8 und 1. Mit anderen Worten: Die Adjazenzmatrix des ursprünglichen Diagramms wird zur Matrix des kürzesten Pfades. Jede Zeile stellt den kürzesten Abstand von jedem Knoten zu anderen Knoten dar.
Okay, das Ergebnis ist in Ordnung, also was genau ist der geschriebene Code? Was ist das für ein K? Machen Sie sich keine Sorgen, schauen wir es uns Schritt für Schritt an.
Angenommen, der Abstand zwischen den beiden Punkten ist nicht der kürzeste, dann muss es einen anderen Punkt als Medium zum Springen geben. Springen Sie zuerst zu diesem Punkt und dann zu Punkt j. Ein solcher Weg ist direkter i liegt in der Nähe von j, wir definieren diesen Punkt als k-Punkt
Aber wir wissen nicht, zu welchem Knoten wir gehen sollen, und es kann sein, dass wir viele k von i bis j durchlaufen müssen Zu diesem Zeitpunkt beginnen wir mit der Traversierung bei k, der ersten Ebene der Schleife. [J ]. Zu diesem Zeitpunkt kennen wir aufgrund der Existenz des äußersten k auch die Länge von k nach j, wenn ich von k aus gehe, was dem Abstand [i][k] + [k][i] entspricht.
Offensichtlich, wenn Der Abstand von [i][k] + [k][i] ist kürzer als [i][j], der Wert von [i][j] wird auf [i][k] + [k] [i] aktualisiert ] Nachdem die internen i- und j-Schleifen von
abgeschlossen sind, ist auch die Durchquerung des ersten Knotens als Mediensprung abgeschlossen. Die Gewichte zwischen jedem Knoten in der aktuellen Matrix wurden über den ersten Knoten verarbeitet Das Medium
Dies ist jedoch nicht korrekt. Möglicherweise ist der Pfad, den wir durch i, k1, k2, j durchlaufen, der kürzeste, sodass die äußere k-Schleife weiterhin durchlaufen wird und die Punkte des zweiten Knotens als Zwischenknoten dienen Der Zyklus wird fortgesetzt, bis alle Knoten die Zwischenknoten einmal durchlaufen haben und wir ein Matrixdiagramm des kürzesten Pfads erhalten. Dies ist das Ergebnis, das in unserem Testcode oben ausgegeben wird.
Nehmen wir Knoten 4 und Knoten 3 wird erklärt. Wir definieren 4 als i und Knoten 3 als j.
初始化时，[i][j] 为 12 ，这个没什么问题，单向图的那条带箭头的边的权值就是 12 。
然后当 k 为 1 时，也就是我们经过结点 1 来看路径有没有变短，这时 [i][k] 是 5 ，[k][j] 是 6 ，OK，路径变成 11 了，把 [i][j] 的值改成 11 。
同时，在 i 为 4 ，j 为 2 的情况下，他们两个的最短路径也在这次 k=1 的循环中被赋值为 7 。最开始 4 到 2 是没有直接的边的，现在在结点 1 的连接下，他们有了路径，也就是 [4][2] = [4][1] + [1][2] = 7 。
当 k 为 2 时，[i][j] 为 11 ，这时 [i][k] 就是上面说过的 [4][2] 。也就是 7 ，而 [k][j] 则是 3 ，路径又缩小了，[i][k] + [k][j] = 10 ，[i][j] 现在又变成了 10 。
循环继续，但已经没有比这条路径更小的值了，所以最后 [4][2] 的最短路径就是 10 。
看着晕吗？拿出笔来在纸上或者本子上自己画画，每一步的 k 都去画一下当前的最短路径矩阵变成什么样了。这样画一次之后，马上就知道这个 Floyd 算法的核心奥秘所在了。
不得不说，前人的智慧真的很伟大吧，不过说是前人，其实 Floyd 大佬在 1962 年才发表了这个算法，但这个算法的核心思想却是数学中的动态规划的思想。所以说，算法和数学是没法分家的，各位大佬哪个不是数学界的一把手呢。
单源最短路径 Dijkstra 算法
说完了多源最短路径，我们再讲一个鼎鼎大名的单源最短路径的算法。虽说上面的多源很牛X，但是它的时间复杂度也就是时间效率也确实是太差了，没看错的话三个 N 次的循环嵌套就是 O(N3)。如果数据稍微多一点的话基本就可以从 Oh!My God! 变成 Oh!FxxK! 了。而且大多数情况下，我们的需求都会是固定的求从某一点到另一点的最短路径问题，也就是单源最短路径问题。这时，就可以使用这种效率稍微好一点的算法来快速地解决了。
// origin 表示源点，也就是我们要看哪个结点到其它结点的最短路径
function Dijkstra($graphArr, $origin)
{
$n = count($graphArr);
$dis = []; // 记录最小值
$book = []; // 记录结点是否访问过
// 初始化源点到每个点的权值
for ($i = 1; $i <= $n; $i++) {
$dis[$i] = $graphArr[$origin][$i]; // 源点到其它点的默认权值
$book[$i] = 0; // 所有结点都没访问过
}
$book[$origin] = 1; // 源点自身标记为已访问
// 核心算法
for ($i = 1; $i <= $n - 1; $i++) {
$min = INFINITY;
// 找到离目标结点最近的结点
for ($j = 1; $j <= $n; $j++) {
// 如果结点没有被访问过，并且当前结点的权值小于 min 值
if ($book[$j] == 0 && $dis[$j] < $min) {
$min = $dis[$j]; // min 修改为当前这个节点的路径值
$u = $j; // 变量 u 变为当前这个结点
}
// 遍历完所有结点，u 就是最近的那个顶点
}
$book[$u] = 1; // 标记 u 为已访问
for ($v = 1; $v <= $n; $v++) {
// 如果 [u][v] 顶点小于无穷
if ($graphArr[$u][$v] < INFINITY) {
// 如果当前 dis[v] 中的权值大于 dis[u]+g[u][v]
if ($dis[$v] > $dis[$u] + $graphArr[$u][$v]) {
// 将当前的 dis[v] 赋值为 dis[u]+g[u][v]
$dis[$v] = $dis[$u] + $graphArr[$u][$v];
}
}
}
// 最近的结点完成，继续下一个最近的结点
}
for ($i = 1; $i <= $n; $i++) {
echo $dis[$i], PHP_EOL;
}
}
// 请输入结点数：4
// 请输入边数：8
// 请输入边，格式为 出 入 权：1 2 2
// 请输入边，格式为 出 入 权：1 3 6
// 请输入边，格式为 出 入 权：1 4 4
// 请输入边，格式为 出 入 权：2 3 3
// 请输入边，格式为 出 入 权：3 1 7
// 请输入边，格式为 出 入 权：3 4 1
// 请输入边，格式为 出 入 权：4 1 5
// 请输入边，格式为 出 入 权：4 3 12
// 测试第四个结点到其它结点的最短路径
Dijkstra($graphArr, 4);
// 5
// 7
// 10
// 0Nach dem Login kopieren
代码一下增加了不少吧，不过仔细看一下核心的算法部分，这次只是两层循环的嵌套了，时间复杂度一下子就降到了 O(N2) ，这一下就比 Floyd 算法提升了很多。当然，它的场景也是有限的，那就是只能一个结点一个结点的计算。
好了，我们还是来看一下 Dijkstra 到底在干嘛吧。我们依然是使用上面那个简单的图，并且还是研究结点 4 到其它结点的算法执行情况。
首先，我们初始化结点 4 到其他所有结点的默认值，这时结点 4 到结点 2 是没有直接路径的，所以是无穷大，而到结点 1 是 5，到结点 3 是 12 。
然后将结点 4 标记为已访问，也就是 book[4] = 1
进入核心算法，从头开始遍历结点，这里是标记为 i 下标，因为这里是单源的最短路径，所以我们不需要再看自己到自己的最短路径了，只需要 n-1 次循环就可以了
开始 j 层的循环，先判断当前的结点是否已经被标记过，没有被标记过的话再看它的值是否是最小的，最后循环完成后获得一个从结点 4 出发的权值最小的路径，并将这条路径到达的结点下标记为 u ，标记 u 下标的这个结点为已访问结点
进入 v 循环，判断图中 u 到 v 的结点是否是无穷，如果不是的话再判断 u 到 v 的结点加上原来的 dis[u] 的权值是否小于 dis[v] 中记录的权值，如果比这个小的话，更新 dis[v] 为 u 到 v 的结点加上原来的 dis[u] 的权值
循环重复地进行比较完成算法
对于结点 4 来说，dis 经历了如下的变化：
首先，默认情况下 dis = [5, 9999999, 12, 0]
第一次循环后，结点1 完成查找，并在 v 的循环中发现了可以从结点1 到结点2 和结点3 而且比原来的值都要小 ，于是 dis = [5, 7, 11, 0]
第二次循环后，结点2 完成查找，这次循环发现从结点2 到结点3 的距离更短，于是 dis = [5, 7, 10, 0]
第三次循环后，结点3 完成查找，没有发现更短的路径，dis = [5, 7, 10, 0]
看明白了吗？不明白的话自己试试吧，不管是断点还是在中间输出一下 dis 和 book ，都能够帮助我们更好地理解这个算法的每一步是如何执行的。从代码中就可以看出来，这个 Dijkstra 算法的时间复杂度是 O(N2) ，这可比 Floyd 快了不少了吧。
总结
关于图的两种最典型的应用及算法就到这里结束了。当然，图的内容可远不止这些，比较典型的还是进度网络图等的算法，特别是做一些项目管理类的系统时会非常有用。当然，更高深的内容就要去研究《图论》了。这个可就远超我的水平了，希望有更多数学相关基础的同学能够继续深入研究。而我嘛，先去恶补下数学吧！！
测试代码：
https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/5.图/source/5.5图的应用：最短路径.php
Nach dem Login kopieren
推荐：《PHP视频教程》
Das obige ist der detaillierte Inhalt vonWas ist der kürzeste Weg in Diagrammanwendungen in der PHP-Datenstruktur?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
