Einführung:
Tatsächlich ist die K-Way-Zusammenführungssortierung immer noch sehr nützlich, vorausgesetzt, Sie möchten große Datenmengen sortieren, z. B. Daten auf TB-Ebene (sagen wir Suchschlüsselwörter auf TB-Ebene). ), Aber unser Speicher ist nur auf GB-Niveau. Wir können nicht alle Daten auf einmal laden und sortieren, aber wir wollen am Ende das Ergebnis, also was sollen wir tun? Tatsächlich handelt es sich hierbei um eine „Teile-und-Herrsche“-Idee. Da wir Q-Zahlen sortieren wollen, aber nicht alle auf einmal sortieren können, teilen wir Q in k auf Gruppen, jede Gruppe ist n. Anzahl, (k Analyse: (1) Wie füge ich k sortierte Arrays zusammen? Da wir bereits über Heaps gesprochen haben, ist die Sortiereffizienz von Heaps offensichtlich sehr hoch. Daher erwägen wir natürlich die Verwendung von Heaps, um sie zu implementieren. Da wir in aufsteigender Reihenfolge sortieren müssen, erstellen wir einen minimalen Heap. Da die Zahlen im endgültigen Sortierergebnis vorne immer kleiner und hinten größer sind, überlegen wir, die ersten Elemente (Mindestzahlen) aller n Arrays in den minimalen Heap zu legen, sodass die Größe des minimalen Heaps k beträgt. Auf diese Weise passen wir die Heap-Struktur an, dann ist ihr erstes Element min (min(array1), min(array2 ....min(arrayn)), was offensichtlich das kleinste Element unter allen Zahlen ist. (2) Da jedes Array in aufsteigender Reihenfolge angeordnet ist, müssen wir, sobald wir ein Mindestelement aus dem Heap löschen, ein Element finden, um die Lücke zu füllen. Dazu müssen wir das nächste Element im Array finden, in dem sich das gelöschte Element befindet, und es dann in den Heap füllen. (Das ist ein bisschen so, als würde man die meisten Elitesoldaten des Landes rekrutieren, um in einem Eliteregiment zu kämpfen. Dann wird der Stärkste aus jedem Regiment rekrutiert. Wenn diese Person unglücklicherweise im Kampf stirbt, dann finde den, der nach ihr zweitgrößter ist Unterstützen Sie diese Elitegruppe weiterhin, um immer die höchste Kampfeffektivität der Elitegruppe aufrechtzuerhalten. Wie findet man also das Array, in dem sich das gelöschte Heap-Element befindet? Dazu müssen wir einen neuen zusammengesetzten Typ erstellen, der sowohl den aktuellen Wert als auch die ID des Arrays enthält, in dem sich der aktuelle Wert befindet. (3) Weil jedes sortierte Array mit dem kontinuierlichen Verlust der kleinsten Elemente versehen ist Nach und nach gibt es weniger Werte, die nicht sortiert wurden, daher müssen wir ein Array der Länge k pflegen, das die aktuelle Position jedes Arrays beibehält, das noch nicht sortiert wurde. Und sobald das kleinste verbleibende Element im Array zum Heap hinzugefügt wird, muss die aktuelle Position nach hinten verschoben werden. (4) Wenn sich die aktuelle Position jedes Arrays nach hinten bewegt, erreicht es schließlich das Ende des Arrays. Zu diesem Zeitpunkt kann das Array keine Zahlen mehr bereitstellen. Es gibt beispielsweise eine scharfe Die Messerfirma in der Armee enthält die herausragendsten Leute. Wenn also die Elitegruppe schließlich ausgewählt wird, wird sie immer aus dieser Firma ausgewählt, und dann wird diese Firma am Ende definitiv niemanden haben), also können wir sie nicht finden Der nächste Wert aus dem Array, in dem sich die aktuell gelöschte Nummer befindet. Zu diesem Zeitpunkt müssen wir die nächste Array-ID mit Wert und ihren Mindestwert auswählen. Die Methode lautet arrayIdForDeletedData = (arrayIdForDeletedData + 1) % k. (5) Am Ende haben alle Array-Positionen das Ende erreicht, das heißt, alle Arrays können keine Werte bereitstellen, die nicht an der Sortierung beteiligt sind. Daher müssen wir zu diesem Zeitpunkt feststellen, ob der aktuelle Heap leer ist nicht, dann enthalten sie die größten Zahlen in n*k. Wir löschenMin(), um die größten Zahlen in der kleinsten Reihenfolge auszugeben. Wenn der aktuelle Heap bereits leer ist, springen Sie direkt aus der Schleife. Die endgültige Zeitkomplexität beträgt also nur O(n*logk) Code: Nachdem wir die oben genannten wichtigen technischen Details durchdacht haben, ist der Code hier einfach zu schreiben. Zuerst definieren wir ein Wertobjekt, das eine Ganzzahl kapselt und aus welchem Array die Ganzzahl stammt. Dann definieren wir einen minimalen Heap, der der Schlüssel zur Lösung des Problems ist Es sollte das oben genannte Wertobjekt sein. Wenn es in den Heap eingefügt und der Heap angepasst wird, werden alle Datenfelder des Wertobjekts berechnet. Abschließend implementieren wir den K-Way-Combiner, der recht einfach zu implementieren ist, bei einigen Indexoperationen ist jedoch besondere Vorsicht geboten. Da wir möchten, dass sie universell sind, werden sowohl k als auch n übergeben. Wenn wir k und n im Voraus planen, müssen wir diese Zahlen tatsächlich überhaupt nicht intern verwalten, da wir sie nur im speichern müssen minimaler Haufen. Experiment: Angenommen, wir haben 32 Zahlen, wir teilen sie in 4 Arten der Zusammenführung auf, jede Art hat 8 Zahlen, und diese 8 Zahlen sind bereits sortiert. Dann verwenden wir den K-Way-Merge-Algorithmus, um alle 32 Zahlen zu sortieren: Das endgültige Laufergebnis ist: Offensichtlich ist das Ergebnis korrekt und unsere Methode unterstützt wiederholte Werte. package com.charles.algo.kwaymerge;
/**
*
* 这个对象表明是一个可以跟踪来自于哪个数组的数据对象
* @author charles.wang
*
*/
public class TrackableData {
//data表明具体的值
private int data;
//comeFromArray表明这个值来自于哪一个数组
private int comeFromArray;
public TrackableData(int data,int comeFromArray){
this.data = data;
this.comeFromArray=comeFromArray;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public int getComeFromArray() {
return comeFromArray;
}
public void setComeFromArray(int comeFromArray) {
this.comeFromArray = comeFromArray;
}
}package com.charles.algo.kwaymerge;
/**
* @author charles.wang
*
*/
public class MinHeap {
// 最小堆的存储是一个数组,并且为了计算，我们第一个位置不放内容
private TrackableData[] data;
// 堆的大小
private int heapSize;
// 当前元素的数量
private int currentSize;
public MinHeap(int maxSize) {
heapSize = maxSize;
// 创建一个比最大容纳数量多1的数组的作用是启用掉数组的头元素，为了方便运算，因为从1开始的运算更加好算
data = new TrackableData[heapSize + 1];
currentSize = 0;
}
/**
* 返回当前的堆是否为空
* @return
*/
public boolean isEmpty(){
if(currentSize==0)
return true;
return false;
}
/**
* 这里考察堆的插入，因为最小堆内部结构中数组前面元素总是按照最小堆已经构建好的，所以我们总从尾部插入 解决方法是： Step
* 1:先把当前的元素插入到数组的尾部 Step 2:递归的比较当前元素和父亲节点元素， Step
* 3:如果当前的元素小于父亲节点的元素，那么就把当前的元素上移，直到移不动为止
*
* @param value
* @return
*/
public MinHeap insert(TrackableData value) {
// 首先判断堆是否满了，如果满了就无法插入
if (currentSize == heapSize)
return this;
// 如果堆还没有满，那么说明堆中还有位置可以插入，我们先找到最后一个可以插入的位置
// currentPos表示当前要插入的位置的数组下标
int currentPos = currentSize + 1;
// 先插入到当前的位置，因为是从1开始的，所以数组下标运算也要+1
data[currentPos] = value;
// 然后比较当前元素和他的父亲元素
// 当前元素是data[currentPos] ，父亲元素是 data[(currentPos/2],一直遍历到根
TrackableData temp;
// 如果currentPos为1，表明是插入的堆中第一个元素，则不用比较
// 否则， 如果插了不止一个元素，则用插入位置的元素和其父元素比较
while (currentPos > 1) {
// 如果当前元素小于父亲元素，那么交换他们位置
if (data[currentPos].getData() < data[currentPos / 2].getData()) {
temp = data[currentPos / 2];
data[currentPos / 2] = data[currentPos];
data[currentPos] = temp;
// 更新当前位置
currentPos = currentPos / 2;
}
// 否则， 在假定已有的堆是最小堆的情况下，说明现在插入的位置是正确的，不用变换
else {
break;
}
}
// 插入完毕之后，吧当前的堆中元素的个数加1
currentSize++;
return this;
}
/**
* 这里考察堆的删除 因为是最小堆，所以肯定删除最小值就是删除堆的根元素，此外，还必须要调整剩余的堆使其仍然保持一个最小堆
* 因为有删除最小元素之后最小元素位置就有了个空位，所以解决方法是： Step 1:吧堆中最后一个元素复制给这个空位 Step
* 2:依次比较这个最后元素值，当前位置的左右子元素的值，从而下调到一个合适的位置 Step 3:从堆数组中移除最后那个元素
*/
public TrackableData deleteMin() {
// 如果最小堆已经为空，那么无法删除最小元素
if (currentSize == 0)
return null;
// 否则堆不为空，那么最小元素总是堆中的第一个元素
TrackableData minValue = data[1];
// 既然删除了最小元素，那么堆中currentSize的尺寸就要-1，为此，我们必须为数组中最后一个元素找到合适的新位置
// 堆中最后一个元素
TrackableData lastValue = data[currentSize];
// 先将堆中最后一个元素移动到最小堆的堆首
data[1] = lastValue;
// 把堆内部存储数组的最后一个元素清0
data[currentSize] = null;
// 并且当前的堆的尺寸要-1
currentSize--;
// 现在开始调整堆结构使其仍然为一个最小堆
int currentPos = 1; // 当前位置设置为根，从根开始比较左右
int leftPos = currentPos * 2;
TrackableData leftValue;
TrackableData rightValue;
TrackableData temp;
// 如果左位置和当前堆的总容量相同，说明只有2个元素了，一个是根元素，一个是根的左元素
if (leftPos == currentSize) {
// 这时候如果根左元素data[2]比根元素data[1]小，那么就交换二者位置
if (data[2].getData() < data[1].getData()) {
temp = data[2];
data[2] = data[1];
data[1] = temp;
}
}
else {
// 保持循环的条件是该节点的左位置小于当前堆中元素个数，那么该节点必定还有右子元素并且位置是左子元素位置+1
while (leftPos < currentSize) {
// 获取当前位置的左子节点的值
leftValue = data[leftPos];
// 获取当期那位置的右子节点的值
rightValue = data[leftPos + 1];
// 如果当前值既小于左子节点又小于右子节点，那么则说明当前值位置是正确的
if (data[currentPos].getData() < leftValue.getData()
&& data[currentPos].getData() < rightValue.getData()) {
break;
}
// 否则，比较左子节点和右子节点
// 如果左子节点小于右子节点（当然了，同时小于当前节点），那么左子节点和当前节点互换位置
else if (leftValue.getData() < rightValue.getData()) {
temp = data[currentPos];
data[currentPos] = leftValue;
data[leftPos] = temp;
// 同时更新当前位置是左子节点的位置,并且新的左子节点的位置为左子节点的左子节点
currentPos = leftPos;
leftPos = currentPos * 2;
}
// 如果右子节点小于左子节点(当然了，同时小于当前节点），那么右边子节点和当前节点互换位置
else {
temp = data[currentPos];
data[currentPos] = rightValue;
data[leftPos + 1] = temp;
// 同时更新当前位置是右子节点的位置,并且新的左子节点的位置为右子节点的左子节点
currentPos = leftPos + 1;
leftPos = currentPos * 2;
}
}
}
return minValue;
}
}package com.charles.algo.kwaymerge;
import java.util.ArrayList;
import java.util.List;
/**
*
* 这个类用于演示K路合并
*
* @author charles.wang
*
*/
public class KWayMerger {
private KWayMerger() {
}
/**
* k路合并，这里的指导思想如下：
*
* (1)首先构造一个最小堆，其中堆中的元素初始值为每个数组中的最小元素
* (2)每次从最小堆中打印并且删除最小元素，然后把这个最小元素所在的数组中的下一个元素插入到最小堆中 (3)每次（2）结束后调整堆来维持这个最小堆
*/
public static void mergeKWay(int k, int n, List<int[]> arrays) {
// 这里存储了所有每个数组的当前的下标,在没有开始插入之前，每个数组的当前下标都设为0
int[] indexInArrays = new int[k];
for (int i = 0; i < k; i++) {
indexInArrays[i] = 0;
}
// 首先构造一个最小堆,其大小为k
MinHeap minHeap = new MinHeap(k);
// 第一步，依次吧每个数组中的第一个元素都插入到最小堆
// 然后把所有数组的下标都指向1
for (int i = 0; i < k; i++) {
// 这里每个都构造TrackableData对象：
// 其中：arrays.get(i)[0]表示它值为第i个数组的下标为0的元素（也就是第i个数组的第一个元素）
// i表示这个对象来自于第i个数组
minHeap.insert(new TrackableData(arrays.get(i)[0], i));
indexInArrays[i] = 1;
}
// 第二步，对最小堆进行反复的插入删除动作
TrackableData currentDeletedData;
TrackableData currentInsertedData;
int arrayIdForDeletedData;
int nextValueIndexInArray;
// 循环的条件是k个数组中至少有一个还有值没有被插入到minHeap中
while (true) {
// 这个变量维护了有多少个数组当前下标已经越界，也就是数组所有元素已经被完全处理过
int noOfArraysThatCompletelyHandled = 0;
// 就是去查询维护所有数组当前下标的数组，如果都越界了，那么就说明都比较过了
for (int i = 0; i < k; i++) {
if (indexInArrays[i] == n)
noOfArraysThatCompletelyHandled++;
}
// 如果所有的数组中的所有的值都比较过了，那么查看堆中内容是否为空。
if (noOfArraysThatCompletelyHandled == k) {
while (!minHeap.isEmpty()) {
currentDeletedData = minHeap.deleteMin();
// 打印出当前的数
System.out.print(currentDeletedData.getData() + " ");
}
break;
}
currentDeletedData = minHeap.deleteMin();
// 打印出当前的数
System.out.print(currentDeletedData.getData() + " ");
// 获取当前的被删的数来自于第几个数组
arrayIdForDeletedData = currentDeletedData.getComeFromArray();
// 获取那个数组的当前下标
nextValueIndexInArray = indexInArrays[arrayIdForDeletedData];
// 如果当前下标没有越界，说明当前数组中还有元素，则找到该数组中的下个元素
if (nextValueIndexInArray < n) {
// 构造新的TrackableData，并且插入到最小堆
currentInsertedData = new TrackableData(
arrays.get(arrayIdForDeletedData)[nextValueIndexInArray],
arrayIdForDeletedData);
minHeap.insert(currentInsertedData);
// 同时更新维护数组当前下标的数组，让对应数组的当前下标+1
indexInArrays[arrayIdForDeletedData]++;
}
// 如果当前下标已经越界，说明这个数组已经没有任何元素了，则找下一个有值的数组的最小元素
else {
while (true) {
arrayIdForDeletedData = (arrayIdForDeletedData + 1) % k;
// 获取那个数组的当前下标
nextValueIndexInArray = indexInArrays[arrayIdForDeletedData];
if (nextValueIndexInArray == n)
continue;
else {
// 构造新的TrackableData，并且插入到最小堆
currentInsertedData = new TrackableData(
arrays.get(arrayIdForDeletedData)[nextValueIndexInArray],
arrayIdForDeletedData);
minHeap.insert(currentInsertedData);
// 同时更新维护数组当前下标的数组，让对应数组的当前下标+1
indexInArrays[arrayIdForDeletedData]++;
break;
}
}
}
}
}
}public static void main(String[] args) {
// 我们来演示K路合并，假设我们有4组已经排序了的数组，每组有8个数，则n=8,k=4
int[] array1 = { 4, 5, 7, 8, 66, 69, 72, 79 };
int[] array2 = { 3, 9, 42, 52, 53, 79, 82, 87 };
int[] array3 = { 1, 17, 21, 31, 47, 55, 67, 95 };
int[] array4 = { 6, 28, 49, 55, 68, 75, 83, 94 };
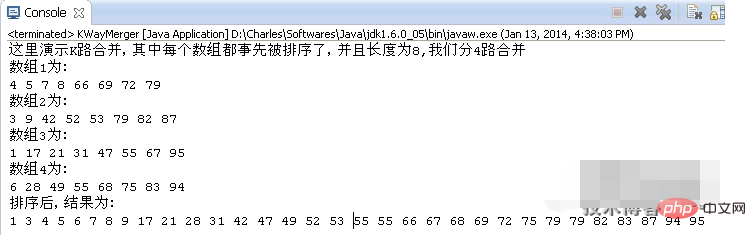
System.out.println("这里演示K路合并，其中每个数组都事先被排序了，并且长度为8,我们分4路合并");
System.out.println("数组1为：");
for(int i=0;i<array1.length;i++)
System.out.print(array1[i]+" ");
System.out.println();
System.out.println("数组2为：");
for(int i=0;i<array2.length;i++)
System.out.print(array2[i]+" ");
System.out.println();
System.out.println("数组3为：");
for(int i=0;i<array3.length;i++)
System.out.print(array3[i]+" ");
System.out.println();
System.out.println("数组4为：");
for(int i=0;i<array4.length;i++)
System.out.print(array4[i]+" ");
System.out.println();
List<int[]> arrayLists = new ArrayList<int[]>(4);
arrayLists.add(0, array1);
arrayLists.add(1, array2);
arrayLists.add(2, array3);
arrayLists.add(3, array4);
KWayMerger kWayMerger = new KWayMerger(4, 8, arrayLists);
System.out.println("排序后，结果为：");
kWayMerger.mergeKWay();
System.out.println();
}
Das obige ist der detaillierte Inhalt vonAusführliche Erklärung der K-Way-Merge-Sortierung (praktischer Kampf). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
Computer-Bluescreen-Code 0xc0000225
Drei Formen bedingter Anweisungen
HTML-Bildcode-Sammlung
Was sind die Unterschiede zwischen Spring-Thread-Pool und JDK-Thread-Pool?
Kompatibilitätsprüfer
So verwenden Sie die Sortierfunktion
So erhalten Sie die aktuelle Uhrzeit in JAVA
Daten von der mobilen Festplatte wiederherstellen
