
Im Computerbereich sind die [Ordner], mit denen wir täglich arbeiten, und die Daten, die wir in Datenbanken speichern, typische Anwendungen von Bäumen. Heute lernen wir die eher theoretischen Definitionen von Bäumen und Binärbäumen sowie einige ihrer Attribute und Eigenschaften kennen.

Anhand der obigen Beispiele aus dem wirklichen Leben können wir sehen, dass die Baumstruktur einige ihrer Eigenschaften zusammenfassen kann.
Baum (Baum) ist eine endliche Menge von N (N>0) Knoten. Es ist entweder ein leerer Baum (N=0) oder ein nicht leerer Baum T.
In dieser Definition müssen wir zwei Punkte klären: Erstens muss der Baum Knoten haben, und zweitens kann er entsprechend der Anzahl der Knoten in zwei Typen unterteilt werden: leere Bäume und nicht leere Bäume. Dies ist jedoch nur die grundlegendste Definition, sie hat einige Eigenschaften.
Es gibt und gibt nur einen Knoten namens Wurzel.
Mit anderen Worten, dieser Baum muss sich von einem bestimmten Knoten aus erweitern, der wie die Wurzel des Baums ist. Von dort aus beginnen sie, sich nach außen zu verzweigen.
Mit Ausnahme des Wurzelknotens können die verbleibenden Knoten in m ( m > 0 ) disjunkte endliche Mengen T1, T2 ..., Tm unterteilt werden. Jede Menge selbst ist ein Baum und wird als Wurzel (SubTree) bezeichnet.
Dieser Absatz ist möglicherweise nicht leicht zu verstehen. Um es ganz klar auszudrücken: Jeder Knoten hat nur einen übergeordneten Knoten und kann nicht mehrere übergeordnete Knoten haben. Ebenso kann es keine Verbindung zwischen horizontalen Knoten geben, es können jedoch mehrere untergeordnete Knoten vorhanden sein.
Für die Definition von Baum können wir uns das Bild unten ansehen.
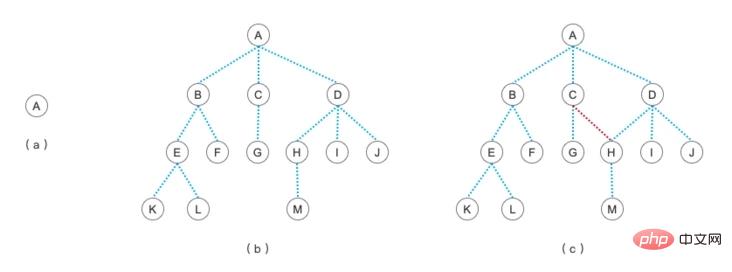
Das Bild oben listet kurz auf, wie Standardbäume und Nicht-Standardbäume aussehen. Darunter:
(a) ist ein Baum mit nur einem Wurzelknoten, solange es einen Knoten gibt, kann er als Baumstruktur bezeichnet werden
(b) ist eine Standardbaumstruktur
(c), beachten Sie, dass es zwischen seinen C- und H-Knoten eine Verbindungslinie gibt. Ein Knoten kann nur dann als Baum bezeichnet werden, wenn er einen übergeordneten Knoten hat [Bild]
Im Vergleich zum Push (in) und Herausspringen aus dem Stapel sowie dem Ein- und Ausreihen in die Warteschlange sind die verwandten Begriffe des Baums viel komplizierter. Auf jeden Fall müssen Sie sich diese Begriffe zunächst merken, sonst wird Sie die Terminologie, die später besprochen wird, nur noch mehr verwirren. Aber es spielt keine Rolle, wenn wir uns im Moment nicht daran erinnern können. Wir können uns zunächst einen groben Eindruck verschaffen und ihn dann später im Lernprozess noch einmal durchgehen.
Knoten: Ein Knoten kann einen Datensatz oder einen Zweig enthalten, der auf andere Knoten zeigt. Er kann als der Ort angesehen werden, an dem die Zweige (b) A, B, C, D, E usw. verzweigen. In der Abbildung sind dies die Grade der Knoten
: Die Anzahl der Teilbäume, die ein Knoten besitzt, wird als Grad des Knotens bezeichnet. Tatsächlich ist es der Grad, wie viele untergeordnete Unterknoten er hat. In der Abbildung beträgt der Grad von Knoten C 1 und der Grad von Knoten D 3
Der Grad des Baums: Der Maximalwert des Grades jedes Knotens im Baum ist der Grad der meisten untergeordneten Knoten. Dies ist der Grad des Baums. (b) Der Grad dieses Baums im Bild beträgt 3
Blätter: Knoten mit Grad 0, dh Knoten ohne untergeordnete Knoten, (b) K, L, F, G , M, im Bild sind I und J die Blattknoten dieses Baums
Eltern und Kinder: Die untergeordneten Knoten eines Knotens sind seine untergeordneten Knoten; für diese untergeordneten Knoten ist der aktuelle Knoten sein übergeordneter Knoten, (b) In Im Bild sind die Kinder von D H, I und J und die Eltern von H, I und J sind D
Ebene: Vom Wurzelknoten aus gezählt, ist der Wurzelknoten die erste Ebene und die Kinder der Wurzel sind Die zweite Ebene usw. (b) Die Ebene des G-Knotens im Bild ist 3, (a) Alle Ebenen im Bild sind nur 1
Die Tiefe (Höhe) des Baums : Die aktuelle maximale Ebene des Baums. Offensichtlich beträgt die Tiefe des (b) Diagramms 4
Brüder, Vorfahren und Nachkommen: Bruderknoten sind die Eltern dieser Knoten, die gleichen Vorfahrenknoten stammen von der Wurzel Knoten zu einem bestimmten Knoten Alle Knoten, die auf der Straße verlaufen, sind alle Knoten auf der Straße, die von einem bestimmten Knoten ausgehen und den Zielknoten erreichen. (b) In der Abbildung sind E und F Brüder, die Vorfahren von E sind A und B und die Nachkommen von E sind K- oder L-Cousins: alle Knoten auf derselben Ebene, aber mit unterschiedlichen Eltern. Sie sind alle Cousins Bild (b), die Cousins von G sind E und F. Darüber hinaus sind H, I und J auch seine Cousins Lernen Sie ein anderes Konzept kennen, das auch die wichtigste Baumform in Datenstrukturen und Algorithmen ist: Binärbäume.
Im Allgemeinen kann sich die Form des Baums ständig ändern. Ein Knoten kann beispielsweise drei untergeordnete Knoten haben, während ein anderer Knoten möglicherweise 300 untergeordnete Knoten hat. Ein solcher Baum ohne Regeln ist tatsächlich sehr mühsam zu bedienen, und die Definition eines Binärbaums ist viel einfacher. Zusätzlich zu den Eigenschaften eines Baums hat er noch einen weiteren Inhalt: Jeder Knoten eines Binärbaums hat höchstens zwei untergeordnete Knoten, das heißt, der Grad des gesamten Binärbaums muss 2 sein, und der Grad aller Knoten darf 2 nicht überschreiten. Warum Binärbäume einfach zu bedienen sind, werden wir im nächsten Abschnitt in den Eigenschaften von Binärbäumen ausführlich erläutern. Alle Baumstrukturen können durch bestimmte regelmäßige Verformungen in Binärbäume umgewandelt werden.
Wir verwenden auch ein Diagramm, um zu zeigen, was ein Binärbaum ist.
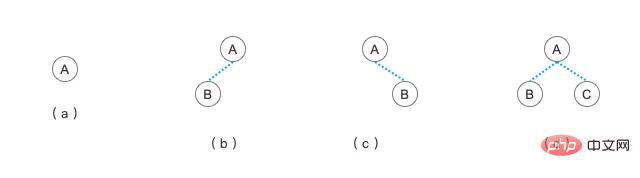
In einem Binärbaum können der linke untergeordnete Knoten und seine Nachkommen als linker Teilbaum des aktuellen Knotens betrachtet werden. Der rechte Knoten und seine Nachkommenknoten können auch als rechter Teilbaum des aktuellen Knotens betrachtet werden. Entsprechend den untergeordneten Knoten des Knotens gibt es mehrere Binärbaumformen, wie in der obigen Abbildung dargestellt.
(a) Ein Baum ist ein Baum mit nur einem Knoten, man kann ihn auch als Binärbaum mit nur einem Knoten bezeichnen
(b) Ein Baum ist ein Binärbaum mit nur einem verbleibenden Knoten
( c) Der Baum ist ein Binärbaum mit nur einem rechten Knoten
(d) Der Baum ist ein Binärbaum mit zwei linken und rechten Knoten
Eigenschaft 1: Auf der i-ten Ebene des Binärbaums gibt es höchstens 2i-1 Knoten (i >= 1)
Eigenschaft 2: Ein Binärbaum mit Tiefe k hat höchstens 2k - 1 Knoten (k >= 1)
Eigenschaft 3: Wenn für jeden Binärbaum T die Anzahl seiner Endknoten n0 und die Anzahl der Knoten mit Grad 2 n2 ist, dann ist n0 = n2 + 1
Eigenschaft 4: Die Tiefe einer vollständigen Binärdatei Baum mit n Knoten ist log2n + 1
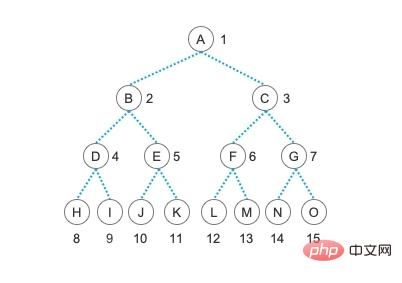
Eigenschaft 5: Wenn die Knoten eines vollständigen Binärbaums mit n Knoten (seine Tiefe ist log2n + 1) in der Reihenfolge der Schichten nummeriert sind (jeweils von der ersten Ebene bis zur log2n + 1. Ebene). Ebene von links nach rechts), dann gilt für jeden A-Knoten i (1
Lassen Sie uns abschließend kurz verstehen, was „Wald“ ist. Mehrere Bäume bilden zusammen einen „Wald“. Genau wie das obige Erklärungsdiagramm des Binärbaums werden (a) (b) (c) (d) als Ganzes betrachtet, es handelt sich um einen „Wald“. In diesem „Wald“ gibt es (a) (b) (c) (d) diese vier Bäume.
Es gibt keine Verbindung zwischen den Bäumen im Wald. Wenn wir einen Wald bewirtschaften oder durchqueren wollen, verwandeln wir den Wald oft in einen Baum. Die spezifischen Algorithmen und Schritte stehen nicht im Mittelpunkt unserer Studie, sodass jeder, der sich eingehend damit befassen möchte, nach relevanten Inhalten suchen oder relevante Lehrbücher konsultieren kann.
Wenn Sie vom Stapel und der Warteschlange hinter den Baum gehen, haben Sie plötzlich das Gefühl, einen großen Schritt gemacht zu haben? Etwas verwirrt? Es spielt keine Rolle, der heutige Inhalt ist eigentlich ein grundlegender theoretischer Inhalt. Wenn Sie ihn verstehen können, verstehen Sie ihn. Wenn Sie ihn nicht verstehen können, lernen Sie weiter und schauen Sie sich dann die heutigen Konzepte an.
Lernen bedeutet nicht, den Prozess des Fortschritts ständig zu wiederholen. Natürlich muss alles auf dem Fundament basieren. Nachdem Sie die Datenstruktur von Bäumen und einige einfache Durchlaufalgorithmen verstanden haben, lernen Sie diese Konzepte noch einmal gründlich kennen und merken Sie sich, dass baumbezogene Fragen in allgemeinen Interviews nicht in Frage kommen.
Empfohlenes Lernen: php-Video-Tutorial
Das obige ist der detaillierte Inhalt vonErfahren Sie in drei Minuten mehr über Bäume und binäre Bäume. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 So öffnen Sie eine PHP-Datei
So öffnen Sie eine PHP-Datei
 So entfernen Sie die ersten paar Elemente eines Arrays in PHP
So entfernen Sie die ersten paar Elemente eines Arrays in PHP
 Was tun, wenn die PHP-Deserialisierung fehlschlägt?
Was tun, wenn die PHP-Deserialisierung fehlschlägt?
 So verbinden Sie PHP mit der MSSQL-Datenbank
So verbinden Sie PHP mit der MSSQL-Datenbank
 So verbinden Sie PHP mit der MSSQL-Datenbank
So verbinden Sie PHP mit der MSSQL-Datenbank
 So laden Sie HTML hoch
So laden Sie HTML hoch
 So lösen Sie verstümmelte Zeichen in PHP
So lösen Sie verstümmelte Zeichen in PHP
 So öffnen Sie PHP-Dateien auf einem Mobiltelefon
So öffnen Sie PHP-Dateien auf einem Mobiltelefon