Mit der Vertiefung des Lernens erweitert und bereichert sich unser Wissen ständig. Hat die Baumstruktur alle verwirrt? Glauben Sie mir, nachdem Sie das Diagramm gelernt haben, werden Sie das Gefühl haben, dass Binärbäume einfach unbeschreiblich einfach sind. Tatsächlich ist der Baum, über den wir sprechen, auch eine spezielle Form eines Diagramms.
Das Konzept der Bilder
Erinnern Sie sich noch an das Bild eines Baumes, das wir im ersten Artikel über das Lernen über Bäume gesehen haben?
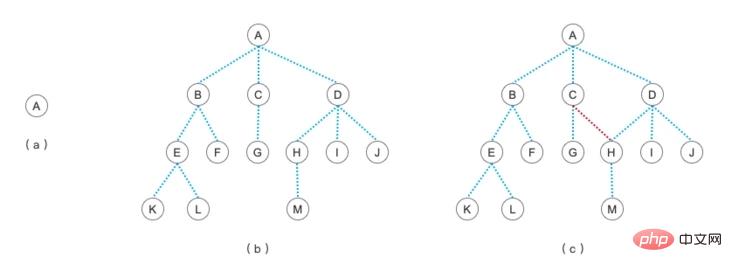
Damals sagten wir, Bild c sei kein Baum, sondern ein Bild. Warum? Aus der Definition von Baum können wir ersehen, dass ein Baum nur einen Wurzelknoten haben kann, dass es keine Verbindung zwischen den Ebenen geben kann und dass er mehrere untergeordnete Knoten haben kann. Graphen müssen diesen Regeln nicht folgen. Das Merkmal von Graphen ist, dass Knoten miteinander verbunden werden können. Die folgenden Bilder sind beispielsweise alle Bilder.
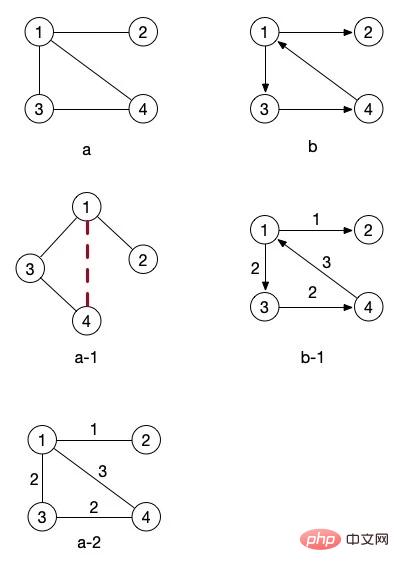
Im oben gezeichneten Bild hat Bild b einen Pfeil, während die Verbindungslinie von Bild a keinen Pfeil hat. Ein Bild mit einer klaren Richtung wie diesem wird als gerichteter Graph bezeichnet. Ein Graph ohne Pfeile, also ein Graph ohne Richtung, wird als ungerichteter Graph bezeichnet.
Lassen Sie uns zunächst auf Abbildung a-1 achten. Tatsächlich dreht es sich nur um Abbildung a. Kann es jeder sehen? Wenn Sie die Verbindung zwischen den Knoten 4 und 1 ignorieren, handelt es sich um einen Baum. Stimmt es mit dem Konzept von Abbildung c in unserem Baumdiagramm oben überein?
Die formellere offizielle Definition eines Graphen lautet:
Graph G besteht aus zwei Mengen V und E, bezeichnet als G=(V, E), wobei V eine endliche, nicht leere Menge von Eckpunkten und E eine endliche Menge ist von Eckpunkten in V, und diese Eckpunkte werden gleichmäßig Kanten genannt.
In einem gerichteten Diagramm kann das Liniensegment, das zwei Punkte vom Startknoten zum Zeigeknoten verbindet, als aufgezeichnet werden. und sind zwei verschiedene Seiten, die auch Bögen genannt werden können. Gemäß Abbildung a können wir sehen, dass es 1> , Da es sich in Abbildung b um einen gerichteten Graphen handelt, hat er nur vier Kanten: , , , .
Haben Sie das Gefühl, dass es klarer ist, wenn Sie sich das Bild oben ansehen, aber Sie sind verwirrt, wenn Sie diese Definition betrachten? Wenn Sie ein Student sind, der einen Test absolvieren muss, müssen Sie sich diese Definition trotzdem merken. Wenn Sie sich wie ich nur auf das Lernen, die Anwendung oder das Verstehen konzentrieren möchten, ist es nicht nötig, es auswendig zu lernen. V ist der Knoten und E ist die Beziehung zwischen diesen Knoten. Die Beziehung zwischen zwei Scheitelpunkten, dh den Liniensegmenten, die die Knoten im Diagramm verbinden, sind die Kanten.
OK, nachdem wir nun diese drei grundlegendsten Konzepte verstanden haben, lernen wir weitere Terminologie im Zusammenhang mit Bildern!
Begriffe im Zusammenhang mit Diagrammen
Zunächst verwenden wir n, um die Anzahl der Eckpunkte im Diagramm darzustellen, und e, um die Anzahl der Kanten darzustellen. Merken Sie sich diese beiden Codes.
(1) Untergraph: Angenommen, es gibt zwei Graphen G=(V, E) und G'=(V', E'). Wenn V' in V und E' in E enthalten ist, heißt es G' ist der Untergraph von G
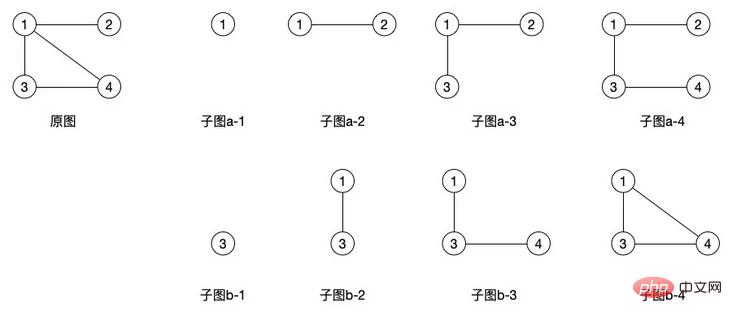
Die Untergraphen rechts im Bild oben sind alle Untergraphen des Originalgraphen. Es ist ersichtlich, dass Untergraphen viele Formen erzeugen können , aber im Vergleich zu ungerichteten Graphen können gerichtete Graphen weniger Untergraphen erzeugen, da ihre Kanten gerichtet sind.
(2) Ungerichteter vollständiger Graph und gerichteter vollständiger Graph: Wenn ein ungerichteter Graph n(n-1)/2 Kanten hat, ist er ein ungerichteter vollständiger Graph. Wenn ein gerichteter Graph n(n-1) Waisen hat, wird er als gerichteter vollständiger Graph bezeichnet. (Siehe den vollständigen Binärbaum)
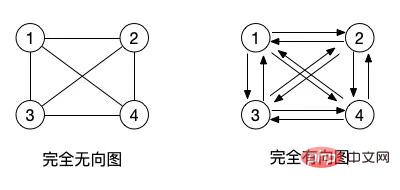
Tatsächlich besteht das Konzept eines vollständigen Diagramms darin, dass alle benachbarten Knoten im Diagramm Kanten haben, die sie miteinander verbinden können.
Für gerichtete Diagramme können wir natürlich auch eine Hin- und Herrichtung definieren, z. B. und Die beiden Pfeile in entgegengesetzter Richtung oben zeigen an, dass es von 1 auf 2 oder von 2 auf 1 gehen kann. In ungerichteten Diagrammen wird eine Kante verwendet, um das Konzept dieser beiden Kanten zu ersetzen. Die Kante ohne Pfeilrichtung ist bidirektional.
(3) Sparse-Graph und dichter Graph: Ein Graph mit wenigen Kanten oder Waisen (wie e
(4) Quanhe.com : In praktischen Anwendungen kann jede Kante oder Insel mit einem Wert markiert werden, der eine gewisse Bedeutung hat, genau wie die Entfernung auf einer Karte. Diese Werte werden als Gewichte bezeichnet. Ein Bild mit Autorität kann als Netzwerk bezeichnet werden
Die Zahlen an den Seiten von Abbildung a-2 und Abbildung b-1 in den oberen Bildern stellen die Gewichte dar. Diese beiden Bilder können als Netzwerkbilder bezeichnet werden. Wir werden das Konzept der Gewichtung später lernen, wenn wir über verwandte Algorithmen sprechen. Anhand dieser beiden Bilder können wir tatsächlich deutlich erkennen, dass wir, wenn wir von Knoten 1 zu Knoten 4 wechseln möchten, nicht direkt zu auf dieser Seite, aber es ist schneller, die Route zu nehmen.
(5) Benachbarte Punkte: Zwei Knoten mit Kanten sind benachbarte Punkte
(6) Grad, In-Grad und Out-Grad: Der Grad eines Scheitelpunkts v bezieht sich auf die Anzahl der mit v verbundenen Kanten. Bei einem gerichteten Graphen ist der Pfeil, der auf andere Knoten zeigt, der äußere Grad, und der Pfeil, der auf sich selbst zeigt, ist der innere Grad.
Schauen wir uns weiterhin Abbildung b an. Knoten 1 hat zwei Out-Degrees und ein In-Degree. Dies scheint keiner großen Erklärung zu bedürfen.
(7) Pfad und Pfadlänge: Alle Scheitelpunkte, die von einem Scheitelpunkt zu einem anderen Scheitelpunkt verlaufen, sind Pfade. Wenn es sich um einen gerichteten Graphen handelt, verläuft sein Pfad in Pfeilrichtung. Die Pfadlänge ist die Anzahl der Kanten oder Waisen, die auf einem Pfad durchlaufen werden
(8) Schleife oder Schleife: Ein Pfad, dessen erster Scheitelpunkt und letzter Scheitelpunkt gleich sind, wird Schleife oder Schleife genannt
(9) verbunden, verbunden Graphen und verbundene Komponenten: Wenn es einen Pfad zwischen zwei Knoten gibt, werden sie als verbunden bezeichnet. Wenn alle Knoten im gesamten Graphen miteinander verbunden werden können, dann ist der Graph ein verbundener Graph. Die Zusammenhangskomponente ist der maximal zusammenhängende Teilgraph im ungerichteten Graphen.
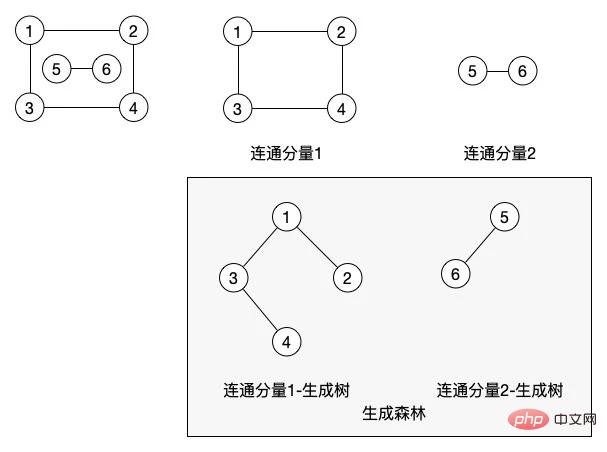
In diesem Bild sind auch die folgenden drei Konzepte enthalten. In einem ungerichteten Graphen ist eine Zusammenhangskomponente gleich einem maximalen Zusammenhangsteilgraphen. In diesem Graphen haben wir zwei Zusammenhangskomponenten.
(10) Maximal verbundener Untergraph: Die maximale Anzahl von Knoten, die ein verbundener Untergraph enthalten kann. Wenn ein weiterer Knoten hinzugefügt wird, ist der Untergraph kein verbundener Graph
(11) Spanning Tree: ein A Der minimal verbundene Teilgraph enthält alle Eckpunkte im Diagramm, aber nur n-1 Kanten, die ausreichen, um einen Baum zu bilden. Ein solcher verbundener Teilgraph ist der Spannbaum eines verbundenen Diagramms. Tatsächlich kann dies über einen Pfad erfolgen Alle Knoten im Diagramm seien in Reihe geschaltet. Im Diagramm verbundener Komponenten generieren wir zwei minimale Spannbäume basierend auf den beiden verbundenen Komponenten. Die Knoten des Spannbaums ihrer verbundenen Komponente 1 müssen nicht unbedingt in dieser Struktur liegen. Wir können Knoten 4 unter Knoten 2 legen, je nachdem, wie wir diesen minimalen Spannbaum durchqueren.
(12) Spanning Forest: In einem nicht verbundenen Diagramm kann jede verbundene Komponente einen verbundenen Spanning Tree erzeugen, der den Spanning Forest des gesamten nicht verbundenen Diagramms darstellt
Sind Sie nach dem Lesen verwirrt? Das spielt keine Rolle, wir werden diese Begriffe in nachfolgenden Studien häufig verwenden und dies ist nicht die umfassendste. Für ein tiefergehendes Studium und Verständnis der graphbezogenen Terminologie können Sie auf die Bibliographie und andere Lernmaterialien zurückgreifen. - Zusammenfassung
Das Konzept der Diagramme ist fast eingeführt. Sie können es verdauen und den folgenden Inhalt weiter studieren. Dies ist erst der Anfang. Viele Schüler werden das Gefühl haben, dass sich dieses Ding im Vergleich zur Baumstruktur erheblich verbessert hat. Haben Sie keine Angst, nachdem Sie die folgenden Kenntnisse erlernt haben, werden Sie auf jeden Fall ein tieferes Verständnis der Baumstruktur haben, auch wenn Sie den Inhalt der Grafik noch nicht verstanden haben. Warum? Bäume sind eigentlich Diagramme ohne Schleifen. Ihre Durchquerung erfolgt durch Tiefe oder Breite, aber das Diagramm ist komplizierter. Haben Sie das Gefühl, dass es noch Hoffnung für die Zukunft gibt? Lernen ist oft ein schrittweiser Prozess. Es wird immer eine Verbindung zwischen aktuellem Wissen und vergangenem Wissen bestehen. Denken Sie nicht zu viel nach, sondern gehen Sie einfach Schritt für Schritt vor!
Empfohlen:
"
Zusammenfassung der PHP-Interviewfragen 2021 (Sammlung)
" "php-Video-Tutorial"
Das obige ist der detaillierte Inhalt vonWas ist das Bild in PHP? Wie kann es gespeichert werden?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
