Die perfekte Begegnung zwischen PHP und der Golden-Section-Sequenz (nicht zu verpassen)

Im Leben enthalten die Dinge, die wir mit bloßem Auge als schön erkennen, oft den Goldenen Schnitt. Zu diesem Zeitpunkt müssen wir seufzen: Die Schönheit der Mathematik ist überall. Die Grenze des Verhältnisses zwischen dem letzten Term und dem vorherigen Term der Goldenen-Schnitt-Folge (auch bekannt als Fibonacci-Folge) ist die Wurzel aus zwei-halb minus eins, was ungefähr 0,618 entspricht (d. h. dem Goldenen-Schnitt-Verhältnis). Wie implementiert man also die Golden-Section-Sequenz mit PHP? Keine Sorge, nehmen wir uns Zeit, es zu verstehen.

Lassen Sie uns zunächst die Goldene-Schnitt-Sequenz (d. h. Fibonacci-Sequenz) verstehen:

Fibonacci-Sequenz bezieht sich auf eine solche Sequenz:

1 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 9 87 1597 2584 4181 6765....

Das heißt: Die ersten beiden Werte sind beide 1, beginnend mit der dritten Ziffer ist jede Ziffer die Summe der ersten beiden Ziffern der aktuellen Ziffer

reguläre Formel Das ist es :

Fn = F(n-1) + F(n+1)

• F: bezieht sich auf die aktuelle Sequenz

• n: der Index der Indexspalte

Okay, ich verstehe Gold Teilen Sie die Sequenz (Fibonacci-Sequenz) auf. Schauen wir uns an, wie Sie sie mit PHP implementieren.

Methode 1: Verwenden Sie das Array

, um die oben angegebene Sequenz zu beobachten. In Kombination mit Array-Kenntnissen können Sie Folgendes analysieren:

• Wenn der Array-Index 0 oder 1 ist, ist der Wert des Elements 1;1；
  

• 数组下标为2时，元素是a[0]+a[1];

• 数组下标为3时，元素是a[1]+a[2];

• .....

• 数组下标为n时，元素是a[n-2]+a[n-1];

可以得出：

• a[0]=1

• a[1]=2

• a[n]=a[n-2]+a[n-1]

Wenn der Array-Index 2 ist, ist das Element a[0]+a[1];

Wenn der Array-Index 3 ist, ist das Element Element ist a [1]+a[2];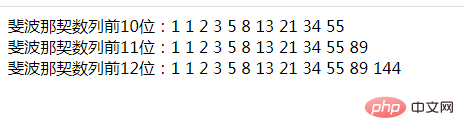

....

Wenn der Array-Index n ist, ist das Element a[n-2] +a[n-1 ];

kann geschlossen werden:

a[0]=1

a[1]=2

🎜🎜a[n]=a[n-2]+a[n-1] (n>2)🎜🎜🎜🎜Code-Implementierung: 🎜

<?php
header("Content-type:text/html;charset=utf-8");
function test($num){
    $arr=[];
    for($i=0;$i<$num;$i++)
    {
        if($i==0 || $i==1){
            $arr[$i]=1;
        }else{
            $arr[$i]=$arr[$i-1]+$arr[$i-2];
        }
		echo $arr[$i]." ";
    }
}
echo "斐波那契数列前10位：";
test(10);
echo "<br>斐波那契数列前11位：";
test(11);
echo "<br>斐波那契数列前12位：";
test(12);
?>

🎜Ausgabe: 🎜🎜🎜🎜🎜Verstehen Nachdem wir nun gelernt haben, wie man Arrays verwendet, um die Fibonacci-Folge zu finden, werfen wir einen Blick darauf, wie man Rekursion verwendet, um die Fibonacci-Folge zu finden. 🎜🎜🎜Methode 2: Rekursion verwenden🎜🎜

<?php
header("Content-type:text/html;charset=utf-8");
function fbnq($n) {
	if ($n <= 0) {
		return 0;
	}
	if ($n == 1 || $n == 2) {
		return 1;
	}
	return fbnq($n - 1) + fbnq($n - 2);
}

echo "斐波那契数列第10位：" . fbnq(10);
echo "<br>斐波那契数列第11位：" . fbnq(11);
echo "<br>斐波那契数列第12位：" . fbnq(12);
?>

🎜Ausgabe: 🎜🎜🎜🎜🎜🎜Die rekursive Methode wurde ebenfalls implementiert, ist das nicht sehr einfach? 🎜🎜Der rekursive Algorithmus kann ein verantwortungsvolles Problem mit kürzerem Code lösen, seine Betriebseffizienz ist jedoch relativ gering. 🎜🎜Okay, das ist alles. Wenn Sie noch etwas wissen möchten, können Sie hier klicken. → →🎜php-Video-Tutorial🎜🎜

Das obige ist der detaillierte Inhalt vonDie perfekte Begegnung zwischen PHP und der Golden-Section-Sequenz (nicht zu verpassen). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!