Was sind die stabilen Sortieralgorithmen?
Zu den stabilen Sortieralgorithmen gehören: 1. Blasensortierung;

Die Betriebsumgebung dieses Tutorials: Windows 10-System, Dell G3-Computer.
Analysieren Sie die Stabilität gängiger Sortieralgorithmen und geben Sie jeweils einfache Gründe an.
Stabiler Sortieralgorithmus:
1. Blasensortierung
Bei der Blasensortierung werden kleine Elemente vorwärts oder große Elemente rückwärts verschoben. Beim Vergleich handelt es sich um einen Vergleich zweier benachbarter Elemente, wobei auch zwischen diesen beiden Elementen ein Austausch stattfindet. Wenn also zwei Elemente gleich sind, glaube ich nicht, dass man sie einfach langweilig vertauschen würde.
Wenn zwei gleiche Elemente nicht benachbart sind, werden sie zu diesem Zeitpunkt nicht ausgetauscht, selbst wenn die beiden durch den vorherigen paarweisen Austausch benachbart sind, sodass sich die Reihenfolge derselben Elemente nicht geändert hat, sodass die Blasensortierung eine A-Stabilität ist Sortieralgorithmus.
2. Auswahlsortierung: Wählen Sie das kleinste aktuelle Element für jede Position aus, wählen Sie das zweitkleinste für das zweite Element unter den verbleibenden Elementen aus. Bis zum n-1-Element muss das n-te Element nicht ausgewählt werden, da es das einzig größte verbleibende Element ist. Wenn dann in einer Auswahl das aktuelle Element kleiner als ein Element ist und das kleine Element nach einem Element erscheint, das dem aktuellen Element entspricht, wird die Stabilität nach dem Austausch zerstört.
5 8 5 2 9 wissen wir beispielsweise, dass die Auswahl des 1ten Elements 5 im ersten Durchgang stimmt überein. Wenn 2 ausgetauscht wird, wird die relative Reihenfolge von 2 und 5 in der Originalsequenz zerstört, also Auswahl Sortieren ist kein stabiler Sortieralgorithmus. n-1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。那么,在一趟选择,如果当前元素比一个元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。
比较拗口,举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中2个5的相对前后顺序就被破坏了,所以选择排序不是一个稳定的排序算法。
3、插入排序
插入排序是在一个已经有序的小序列的基础上,一次插入一个元素。当然,刚开始这个有序的小序列只有1个元素,就是第一个元素。比较是从有序序列的末尾开始,也就是想要插入的元素和已经有序的最大者开始比起,如果比它大则直接插入在其后面,否则一直往前找直到找到它该插入的位置。
如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。
所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
4、快速排序
快速排序有两个方向,左边的i下标一直往右走,当a[i] <= a[center_index],其中center_index是中枢元素的数组下标,一般取为数组第0个元素。而右边的j下标一直往左走,当a[j]>a[center_index]。
如果i和j都走不动了,i<=j,交换a[i]和a[j],重复上面的过程,直到i>j。交换a[j]和a[center_index],完成一趟快速排序。在中枢元素和a[j]交换的时候,很有可能把前面的元素的稳定性打乱,比如序列为5 3 3 4 3 8 9 10 11,现在中枢元素5和3(第5个元素,下标从1开始计)交换就会把元素3的稳定性打乱,所以快速排序是一个不稳定的排序算法,不稳定发生在中枢元素和a[j] 交换的时刻。
5、归并排序
归并排序是把序列递归地分成短序列,递归出口是短序列只有1个元素(认为直接有序)或者2个序列(1次比较和交换),然后把各个有序的段序列合并成一个有序的长序列,不断合并直到原序列全部排好序。可以发现,在1个或2个元素时,1个元素不会交换,2
Einfügungssortierung fügt jeweils ein Element basierend auf einer bereits geordneten kleinen Sequenz ein. Natürlich hatte diese kleine geordnete Sequenz am Anfang nur ein Element, nämlich das erste Element. Der Vergleich beginnt am Ende der geordneten Sequenz, das heißt, das Element, das Sie einfügen möchten, wird mit dem größten, bereits sortierten Element verglichen. Wenn es größer ist, fügen Sie es direkt dahinter ein, andernfalls schauen Sie weiter, bis Sie es gefunden haben Finden Sie das Element, in das es eingefügt werden soll.
Wenn Sie auf ein Element stoßen, das dem eingefügten Element entspricht, fügt das eingefügte Element das einzufügende Element nach dem gleichen Element ein. Die Reihenfolge gleicher Elemente hat sich also nicht geändert. Die Reihenfolge der ursprünglichen ungeordneten Reihenfolge ist die Reihenfolge nach der Sortierung, sodass die Einfügungssortierung stabil ist.
4. Schnellsortierung🎜Die Schnellsortierung auf der linken Seite geht ganz nach rechts. Dabei istcenter_index der Array-Index des mittleren Elements, das im Allgemeinen als 0-Element des Arrays verwendet wird. Der j-Index auf der rechten Seite geht ganz nach links, wenn a[j]>a[center_index]. 🎜🎜Wenn sowohl i als auch j nicht laufen können, i<=j, tauschen Sie a[i] und a[j] aus, wiederholen Sie den Vorgang Der obige Vorgang wird bis i>j fortgesetzt. Tauschen Sie a[j] und a[center_index] aus, um eine schnelle Sortierung durchzuführen. Wenn das Pivot-Element mit a[j] ausgetauscht wird, ist es sehr wahrscheinlich, dass die Stabilität des vorherigen Elements gestört wird. Die Reihenfolge lautet beispielsweise 5 3 3 4 3 8 9 10 11, jetzt die Hub-Elemente 5 und 3 (das 5-Element, der Index beginnt bei 1 code>) werden ausgetauscht. Dadurch wird die Stabilität von Element 3 gestört, daher ist die schnelle Sortierung ein instabiler Sortieralgorithmus. Die Instabilität tritt in dem Moment auf, in dem das zentrale Element und a[j] ausgetauscht werden. 🎜🎜🎜5. Zusammenführungssortierung🎜🎜🎜Bei der Zusammenführungssortierung wird die Sequenz rekursiv in kurze Sequenzen unterteilt. Der rekursive Ausgang besteht darin, dass die kurze Sequenz nur <code>1-Elemente (als direkt geordnet betrachtet) oder 2 code> Sequenzen (1 Vergleich und Austausch) und dann jede geordnete Segmentsequenz zu einer geordneten langen Sequenz zusammenführen und mit dem Zusammenführen fortfahren, bis alle Originalsequenzen sortiert sind. Es kann festgestellt werden, dass bei 1- oder 2-Elementen 1-Elemente nicht ausgetauscht werden und 2 Elemente werden nicht ausgetauscht, wenn die Größen gleich sind und niemand sie absichtlich vertauscht, beeinträchtigt dies nicht die Stabilität. 🎜🎜Wird also beim Zusammenführen kurzer geordneter Sequenzen die Stabilität zerstört? 🎜🎜Nein, während des Zusammenführungsprozesses können wir sicherstellen, dass wir bei Gleichheit der beiden aktuellen Elemente das Element der vorherigen Sequenz vor der Ergebnissequenz speichern und so die Stabilität gewährleisten. Daher ist die Zusammenführungssortierung auch ein stabiler Sortieralgorithmus. 🎜🎜🎜6. Radix-Sortierung: Zuerst nach niedriger Reihenfolge sortieren und dann nach hoher Reihenfolge sortieren;Und so weiter, bis zur höchsten Position. Manchmal haben einige Attribute eine Prioritätsreihenfolge. Sie werden zuerst nach niedriger Priorität und dann nach hoher Priorität sortiert. Die letzte Reihenfolge ist, dass diejenigen mit hoher Priorität zuerst kommen und diejenigen mit der gleichen hohen und niedrigen Priorität zuerst. Die Radix-Sortierung basiert auf separater Sortierung und separater Sammlung und ist daher ein stabiler Sortieralgorithmus.
7. Hügelsortierung (Shell)
Bei der Hügelsortierung werden Elemente nach unterschiedlichen Schrittlängen eingefügt und sortiert. Wenn die Elemente zu Beginn sehr ungeordnet sind, ist die Schrittgröße am größten, also die Anzahl der Elemente Die Einfügungssortierung ist sehr groß und sehr schnell.
Wenn die Elemente grundsätzlich geordnet sind und die Schrittgröße klein ist, ist die Einfügungssortierung für geordnete Sequenzen sehr effizient. Daher ist die zeitliche Komplexität der Hill-Sortierung besser als bei O(n^2). Aufgrund der mehrfachen Einfügungssortierung wissen wir, dass eine Einfügungssortierung stabil ist und die relative Reihenfolge derselben Elemente nicht ändert. Bei verschiedenen Einfügungssortierungsprozessen können sich jedoch dieselben Elemente in ihren jeweiligen Einfügungssortierungen bewegen, und letztendlich ändert sich auch ihre Stabilität Wechselgeld ist durcheinander, sodass die Shell-Sortierung instabil ist. O(n^2)好一些。由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以shell排序是不稳定的。
8、堆排序
我们知道堆的结构是节点i的孩子为2 * i和2 * i + 1节点,大顶堆要求父节点大于等于其2个子节点,小顶堆要求父节点小于等于其2个子节点。在一个长为n的序列,堆排序的过程是从第n / 2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n / 2-1, n/2-2,...1这些个父节点选择元素时,就会破坏稳定性。有可能第n/2个父节点交换把后面一个元素交换过去了,而第n/2-1
i 2 * i und 2 * i sind + 1 Knoten erfordert ein großer oberer Heap, dass der übergeordnete Knoten größer oder gleich seinen 2 untergeordneten Knoten ist, und ein kleiner oberer Heap erfordert, dass der übergeordnete Knoten kleiner oder gleich ist zu seinen 2 untergeordneten Knoten. In einer Sequenz der Länge n besteht der Prozess der Heap-Sortierung darin, den größten Wert ab n / 2 und seine untergeordneten Knoten insgesamt 3auszuwählen > (Großer oberer Heap) oder kleinster (kleiner oberer Heap), die Wahl zwischen diesen 3 Elementen wird die Stabilität sicherlich nicht zerstören. Wenn jedoch Elemente für die übergeordneten Knoten n / 2-1, n/2-2, ...1 ausgewählt werden, wird die Stabilität zerstört . Es ist möglich, dass der n/2te Elternknoten das folgende Element austauscht, während der n/2te Elternknoten das folgende identische Element nicht austauscht die Stabilität zwischen diesen beiden identischen Elementen wird zerstört. Daher ist die Heap-Sortierung kein stabiler Sortieralgorithmus. 🎜🎜Weitere Informationen zu diesem Thema finden Sie in der Spalte „FAQ🎜“! 🎜Das obige ist der detaillierte Inhalt vonWas sind die stabilen Sortieralgorithmen?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Dreamweaver CS6
Visuelle Webentwicklungstools

SublimeText3 Mac-Version
Codebearbeitungssoftware auf Gottesniveau (SublimeText3)

Heiße Themen
 1392
1392
 52
52
 Komplexe experimentelle Designprobleme im zweiseitigen Markt von Kuaishou
Apr 15, 2023 pm 07:40 PM
Komplexe experimentelle Designprobleme im zweiseitigen Markt von Kuaishou
Apr 15, 2023 pm 07:40 PM
1. Hintergrund des Problems 1. Einführung in das zweiseitige Marktexperiment Der zweiseitige Markt, also eine Plattform, umfasst zwei Teilnehmer, Produzenten und Verbraucher, und beide Parteien fördern sich gegenseitig. Kuaishou hat beispielsweise einen Videoproduzenten und einen Videokonsumenten, und die beiden Identitäten können sich bis zu einem gewissen Grad überschneiden. Bilaterales Experiment ist eine experimentelle Methode, die Gruppen auf Produzenten- und Verbraucherseite vereint. Bilaterale Experimente haben folgende Vorteile: (1) Die Auswirkungen der neuen Strategie auf zwei Aspekte können gleichzeitig erfasst werden, beispielsweise Änderungen im Produkt-DAU und die Anzahl der Personen, die Werke hochladen. Bilaterale Plattformen haben oft netzwerkübergreifende Effekte, je mehr Leser es gibt, desto aktiver werden die Autoren sein, und je aktiver die Autoren sind, desto mehr Leser werden ihnen folgen. (2) Effektüberlauf und -übertragung können erkannt werden. (3) Helfen Sie uns, den Wirkungsmechanismus besser zu verstehen. Das AB-Experiment selbst kann uns nicht nur den Zusammenhang zwischen Ursache und Wirkung aufzeigen
 So filtern und sortieren Sie Daten in der Vue-Technologieentwicklung
Oct 09, 2023 pm 01:25 PM
So filtern und sortieren Sie Daten in der Vue-Technologieentwicklung
Oct 09, 2023 pm 01:25 PM
So filtern und sortieren Sie Daten in der Vue-Technologieentwicklung. In der Vue-Technologieentwicklung sind das Filtern und Sortieren von Daten sehr häufige und wichtige Funktionen. Durch Datenfilterung und -sortierung können wir die benötigten Informationen schnell abfragen und anzeigen und so die Benutzererfahrung verbessern. In diesem Artikel wird das Filtern und Sortieren von Daten in Vue vorgestellt und spezifische Codebeispiele bereitgestellt, um den Lesern zu helfen, diese Funktionen besser zu verstehen und zu verwenden. 1. Datenfilterung Datenfilterung bezieht sich auf das Herausfiltern von Daten, die den Anforderungen basierend auf bestimmten Bedingungen entsprechen. In Vue können wir comp bestehen
 Google nutzt KI, um das Zehn-Jahres-Ranking-Algorithmus-Siegel zu brechen. Es wird jeden Tag Billionen Mal ausgeführt, aber Internetnutzer sagen, es sei die unrealistischste Forschung?
Jun 22, 2023 pm 09:18 PM
Google nutzt KI, um das Zehn-Jahres-Ranking-Algorithmus-Siegel zu brechen. Es wird jeden Tag Billionen Mal ausgeführt, aber Internetnutzer sagen, es sei die unrealistischste Forschung?
Jun 22, 2023 pm 09:18 PM
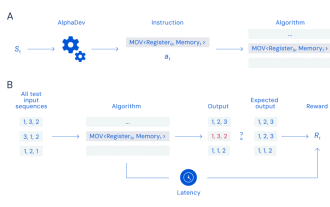
Organisieren |. Nuka-Cola, Chu Es ist eine interessante Herausforderung und es gibt viele Möglichkeiten, sie zu meistern. Es wurde viel Zeit investiert, um herauszufinden, wie Sortieraufgaben effizienter erledigt werden können. Als Grundoperation sind Sortieralgorithmen in die Standardbibliotheken der meisten Programmiersprachen integriert. Es gibt viele verschiedene Sortiertechniken und Algorithmen, die in Codebasen auf der ganzen Welt verwendet werden, um große Datenmengen online zu organisieren, aber zumindest was die mit dem LLVM-Compiler verwendeten C++-Bibliotheken betrifft, hat sich der Sortiercode seit mehr als einem Jahr nicht geändert Jahrzehnt. Kürzlich hat das Google DeepMindAI-Team nun eine entwickelt
 So verwenden Sie den Radix-Sortieralgorithmus in C++
Sep 19, 2023 pm 12:15 PM
So verwenden Sie den Radix-Sortieralgorithmus in C++
Sep 19, 2023 pm 12:15 PM
So verwenden Sie den Basissortieralgorithmus in C++. Der Basissortierungsalgorithmus ist ein nicht vergleichender Sortieralgorithmus, der die Sortierung durch Aufteilen der zu sortierenden Elemente in einen begrenzten Satz von Ziffern abschließt. In C++ können wir den Radix-Sortieralgorithmus verwenden, um eine Menge von Ganzzahlen zu sortieren. Im Folgenden besprechen wir anhand konkreter Codebeispiele ausführlich, wie der Basissortieralgorithmus implementiert wird. Algorithmusidee Die Idee des Radix-Sortieralgorithmus besteht darin, die zu sortierenden Elemente in einen begrenzten Satz digitaler Bits zu unterteilen und die Elemente dann nacheinander nach jedem Bit zu sortieren. Die Sortierung nach jedem Bit ist abgeschlossen
 So implementieren Sie den Auswahlsortierungsalgorithmus in C#
Sep 20, 2023 pm 01:33 PM
So implementieren Sie den Auswahlsortierungsalgorithmus in C#
Sep 20, 2023 pm 01:33 PM
So implementieren Sie den Auswahlsortierungsalgorithmus in C#. Die Auswahlsortierung (SelectionSort) ist ein einfacher und intuitiver Sortieralgorithmus. Seine Grundidee besteht darin, jedes Mal das kleinste (oder größte) Element aus den zu sortierenden Elementen auszuwählen und am Ende einzufügen die sortierte Reihenfolge. Wiederholen Sie diesen Vorgang, bis alle Elemente sortiert sind. Erfahren Sie mehr darüber, wie Sie den Auswahlsortierungsalgorithmus in C# implementieren, zusammen mit spezifischen Codebeispielen. Erstellen einer Auswahlsortierungsmethode Zuerst müssen wir eine Methode zur Implementierung der Auswahlsortierung erstellen. Diese Methode akzeptiert a
 Swoole Advanced: So verwenden Sie Multithreading, um einen Hochgeschwindigkeits-Sortieralgorithmus zu implementieren
Jun 14, 2023 pm 09:16 PM
Swoole Advanced: So verwenden Sie Multithreading, um einen Hochgeschwindigkeits-Sortieralgorithmus zu implementieren
Jun 14, 2023 pm 09:16 PM
Swoole ist ein leistungsstarkes Netzwerkkommunikations-Framework, das auf der PHP-Sprache basiert. Es unterstützt die Implementierung mehrerer asynchroner E/A-Modi und mehrerer erweiterter Netzwerkprotokolle. Basierend auf Swoole können wir seine Multithreading-Funktion nutzen, um effiziente Algorithmusoperationen zu implementieren, beispielsweise Hochgeschwindigkeits-Sortieralgorithmen. Der Hochgeschwindigkeits-Sortieralgorithmus (QuickSort) ist ein gängiger Sortieralgorithmus. Durch die Lokalisierung eines Benchmark-Elements werden die Elemente, die kleiner als das Benchmark-Element sind, auf der linken Seite platziert, und diejenigen, die größer oder gleich dem Benchmark sind Element werden auf der rechten Seite platziert. Dann werden die linke und die rechte Teilsequenzrekursion platziert
 Welche Sortieralgorithmen gibt es für Arrays?
Jun 02, 2024 pm 10:33 PM
Welche Sortieralgorithmen gibt es für Arrays?
Jun 02, 2024 pm 10:33 PM
Array-Sortieralgorithmen werden verwendet, um Elemente in einer bestimmten Reihenfolge anzuordnen. Zu den gängigen Arten von Algorithmen gehören: Blasensortierung: Vertauschen Sie Positionen durch Vergleichen benachbarter Elemente. Auswahlsortierung: Finden Sie das kleinste Element und tauschen Sie es an die aktuelle Position aus. Einfügungssortierung: Elemente einzeln an der richtigen Position einfügen. Schnelle Sortierung: Divide-and-Conquer-Methode, wählen Sie das Pivot-Element aus, um das Array zu teilen. Zusammenführungssortierung: Teilen und Erobern, rekursives Sortieren und Zusammenführen von Unterarrays.
 Diskussion über Anwendungsszenarien verschiedener PHP-Array-Sortieralgorithmen
Apr 28, 2024 am 09:39 AM
Diskussion über Anwendungsszenarien verschiedener PHP-Array-Sortieralgorithmen
Apr 28, 2024 am 09:39 AM
Für verschiedene Szenarien ist es entscheidend, den geeigneten PHP-Array-Sortieralgorithmus auszuwählen. Die Blasensortierung eignet sich für kleine Arrays ohne Stabilitätsanforderungen. Die schnelle Sortierung weist in den meisten Fällen eine hohe Stabilität auf und eignet sich für Situationen, in denen stabile Ergebnisse erforderlich sind ; Heap-Sortierung findet effizient den Maximal- oder Minimalwert. Durch den Vergleich tatsächlicher Fälle ist die schnelle Sortierung anderen Algorithmen hinsichtlich der Zeiteffizienz überlegen. Wenn jedoch Stabilität berücksichtigt werden muss, sollte die Zusammenführungssortierung gewählt werden.



