Vertiefendes Verständnis der MySQL-Indexstruktur

Dieser Artikel vermittelt Ihnen relevantes Wissen über MySQL und stellt hauptsächlich verwandte Fragen zur Indexstruktur vor. Wie ist also die Struktur des Index? Warum kann die Indizierung so schnell sein? Werfen wir einen Blick unten, ich hoffe, es wird für alle hilfreich sein.

Empfohlenes Lernen: MySQL-Tutorial

Datenbankspeichereinheit

Zunächst müssen wir wissen, dass der Index beim Abfragen über den Index nur auf der Festplatte gespeichert werden kann, um Persistenz zu erreichen Da auf der Festplatte E/A-Vorgänge generiert werden, ist es beim Entwerfen des Index erforderlich, die Anzahl der Suchvorgänge so weit wie möglich zu reduzieren, um die E/A-Zeit zu verkürzen.

Darüber hinaus müssen Sie ein sehr wichtiges Prinzip kennen: Die Grundeinheit des Datenbankverwaltungsspeicherplatzes ist Seite (Seite), und mehrere Zeilendatensätze (Zeile) werden auf einer Seite gespeichert. 页(Page)，一个页中存储多条行记录(Row)。

计算机系统对磁盘 I/O 会做预读优化，当一次I/O时，除了当前磁盘地址的数据以外，还会把相邻的数据也读取到内存缓冲池中，每一次 I/O 读取的数据成为一页，InnoDB 默认的页大小是 16KB。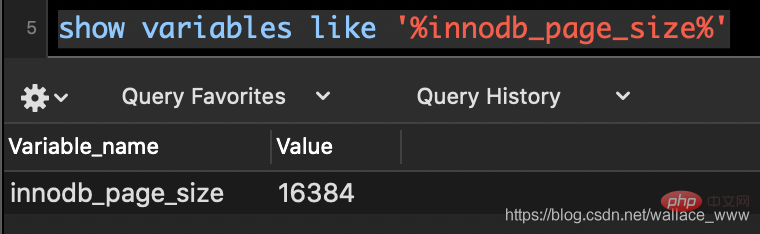
连续的 64 个页组成一个区(Extent)，一个或多个区组成一个段(Segment)，一个或多个段组成表空间(Tablespace)。InnoDB 有两种表空间类型，共享表空间表示多张表共享一个表空间，独立表空间表示每张表的数据和索引全部存在独立的表空间中。

数据页结构如下（图源：极客时间《MySQL 必知必会》）：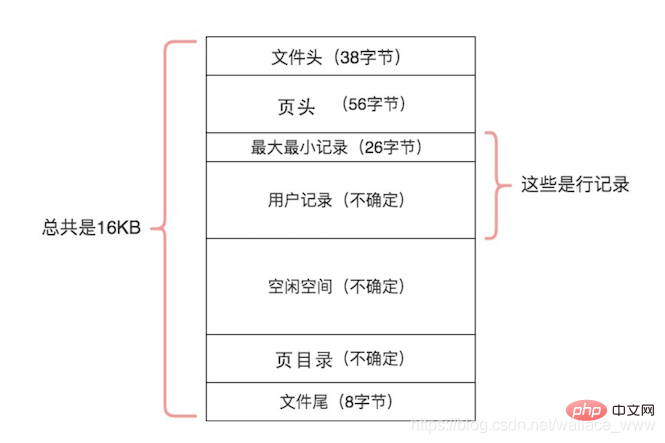

数据页的 7 个结构内容可以大致分为以下三类：

• 文件通用部分，用于校验页传输完整
  • 文件头（File Header）: 表述页信息，文件头中使用 FIL_PAGE_PREV 和 FIL_PAGE_NEXT 构成一个双向链表，分别指向前后的数据页。
  • 页头（File Header）：记录页的状态信息
  • 文件尾（File Trailer）: 校验页是否完整
• 记录部分，用于存储数据记录
  • 最大最小记录（Infimum/Supremum）：虚拟的行记录，表示数据页的最大记录和最小记录。
  • 用户记录（User Record）和空闲空间（Free Space）: 用于存储数据行记录内容
• 索引部分，用于提高记录的检索效率
  • 页目录（Page Directory）：存储用户记录的相对位置

详情可参考淘宝的数据库内核月报

索引数据结构

很自然的，我们会想到查找算法中涉及到的一些常用数据结构，比如二叉查找树，二叉平衡树等等，实际上，Innodb 的索引是用 B+ 树

Das Computersystem führt eine Vorauslese-Optimierung für Festplatten-E/A durch. Wenn eine E/A durchgeführt wird, werden zusätzlich zu den Daten an der aktuellen Festplattenadresse auch angrenzende Daten in die gelesen Im Speicherpuffer werden die von jeder E/A gelesenen Daten zu einer Seite, und die Standardseitengröße von InnoDB beträgt 16 KB.

64 aufeinanderfolgende Seiten bilden einen Extent, ein oder mehrere Extents bilden ein Segment und ein oder mehrere Segmente bilden einen Tablespace. InnoDB verfügt über zwei Tabellenbereichstypen. Dies bedeutet, dass mehrere Tabellen einen Tabellenbereich gemeinsam nutzen. Unabhängiger Tabellenbereich bedeutet, dass die Daten und Indizes jeder Tabelle in unabhängigen Tabellenbereichen gespeichert werden.

Die Datenseitenstruktur ist wie folgt (Quelle: Geek Time „Must Know MySQL“):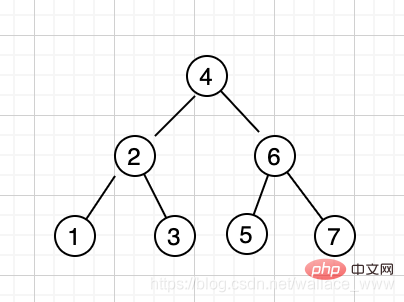
Die 7 strukturellen Inhalte der Datenseite lassen sich grob in die folgenden drei Kategorien einteilen:

• Allgemeiner Teil der Datei, der verwendet wird, um zu überprüfen, ob die Die Seitenübertragung ist abgeschlossen
• Dateikopf: Drückt Seiteninformationen aus. FIL_PAGE_PREV und FIL_PAGE_NEXT werden im Dateikopf verwendet, um eine doppelt verknüpfte Liste zu bilden, die auf die vorherige bzw. nächste Datenseite verweist.
• Dateikopfzeile: Statusinformationen der Seite aufzeichnen
• Dateitrailer: Überprüfen Sie, ob die Seite vollständig ist

Der Datensatz Teil wird zum Speichern von Datensätzen verwendet

• Maximale und minimale Datensätze (Infimum/Supremum): virtuelle Zeilendatensätze, die den maximalen Datensatz und den minimalen Datensatz der Datenseite darstellen.
• Benutzerdatensatz und freier Speicherplatz: Wird zum Speichern des Inhalts von Datenzeilendatensätzen verwendet.

Indexteil, der zur Verbesserung der Effizienz beim Abrufen von Datensätzen verwendet wird

• Seitenverzeichnis: Speichert den relativen Standort von Benutzerdatensätzen

Weitere Informationen finden Sie im monatlichen Bericht des Datenbankkerns von Taobao.
Struktur der Indexdaten

Natürlich werden wir denken Einige gängige Datenstrukturen, die an Suchalgorithmen beteiligt sind, wie z. B. binäre Suchbäume, binär ausgeglichene Bäume usw. Tatsächlich verwendet der Index von Innodb B+-Baum, um dies zu erreichen. Schauen wir uns an, warum diese Indexstruktur so war gewählt.

Einschränkungen des Binärbaums

Lassen Sie uns zunächst kurz die Definition des Binärsuchbaums betrachten. Wenn der zu findende Schlüssel größer als der Wurzelknoten ist, suchen Sie im rechten Teilbaum kleiner als der Wurzelknoten ist, suchen Sie im linken Teilbaum, bis der Schlüssel gefunden wird. Die Zeitkomplexität beträgt O(logn). Beispielsweise generiert die Sequenz [4,2,6,1,3,5,7] den folgenden binären Suchbaum:

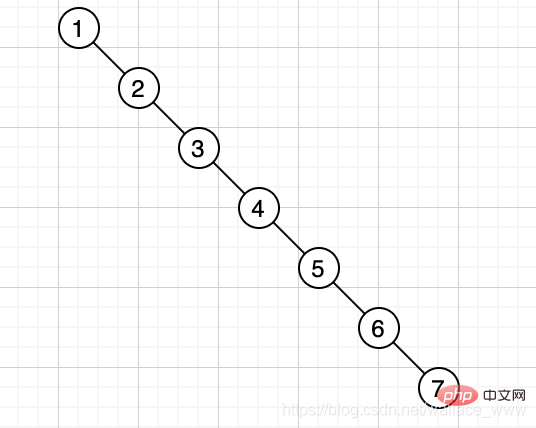
In einigen Sonderfällen ist die Tiefe des Binärbaums jedoch sehr groß, z Als [1,2, 3,4,5,6,7] wird der folgende Baum generiert:

🎜🎜 In der folgenden Situation dauert es im schlimmsten Fall 7 Mal, bis das gewünschte Ergebnis und die Abfrage gefunden sind Die Zeit wird zu Es ist O(n). 🎜🎜Um diese Situation zu optimieren, gibt es einen ausgeglichenen binären Suchbaum (AVL-Baum). Ein AVL-Baum bezieht sich auf einen Baum, in dem der Höhenunterschied zwischen dem linken und rechten Teilbaum 1 nicht überschreitet. Die Suchzeitkomplexität beträgt O (logn), was bereits der Fall ist Es ist ein relativ idealer Suchbaum, aber in einer Datenbank mit mehreren zehn Millionen Datensatzzeilen ist die Tiefe des Baums immer noch sehr hoch und es ist immer noch nicht die idealste Struktur. 🎜🎜B-Baum🎜🎜Wenn Sie also von einem Binärbaum zu einem N-Ary-Baum erweitern, kann man sich leicht vorstellen, dass der N-Ary-Baum die Tiefe des Baums erheblich reduzieren kann Die Struktur kann bereits Dutzende Terabyte an Daten unterstützen. 🎜🎜B-Baum (Balance Tree) ist ein solcher N-Baum, der auch B-Baum genannt wird und die folgende Definition erfüllt: 🎜 Sei k der Grad des B-Baums und gibt an, wie viele Kinder jeder Knoten hat kann höchstens einen Knoten haben), 🎜

1. Jeder Festplattenblock enthält höchstens k - 1 个关键字 和 k Zeiger auf untergeordnete Knoten.
2. In Blattknoten gibt es nur Schlüsselwörter und keine untergeordneten Knotenzeiger der linke Teilbaum eines Wortes ist kleiner als dieser, und alle Schlüssel im rechten Teilbaum sind größer als dieser.
3. Alle Blattknoten befinden sich auf derselben Ebene.
4. Wie oben erwähnt, liest jede E/A die Daten eines Plattenblocks vor, der eine Seite groß ist. Der Inhalt eines Plattenblocks wird zur Darstellung einer E/A verwendet. Der Baum ist wie folgt (Quelle: Ji Sie müssen SQL in Gastzeit kennen):

Der B-Baum ist ebenfalls geordnet. Da der Zeiger des untergeordneten Knotens um 1 größer sein muss als das Schlüsselwort, kann das Schlüsselwort zum Teilen der Segmente verwendet werden Wie im Beispiel in der Abbildung hat jeder A-Knoten 2 Schlüsselwörter und 3 untergeordnete Knoten, z. B. Plattenblock 2. Das Schlüsselwort 3, 5 des ersten Bytepunkts ist kleiner als sein eigener erster untergeordneter Knoten 8, und die 9, 10 des zweiten untergeordneten Knotens liegt zwischen 8 und 10. Zwischen 12 und 12 beträgt der Wert des dritten untergeordneten Knotens 13 und 15, was größer ist als der Wert seines zweiten untergeordneten Knotens 12.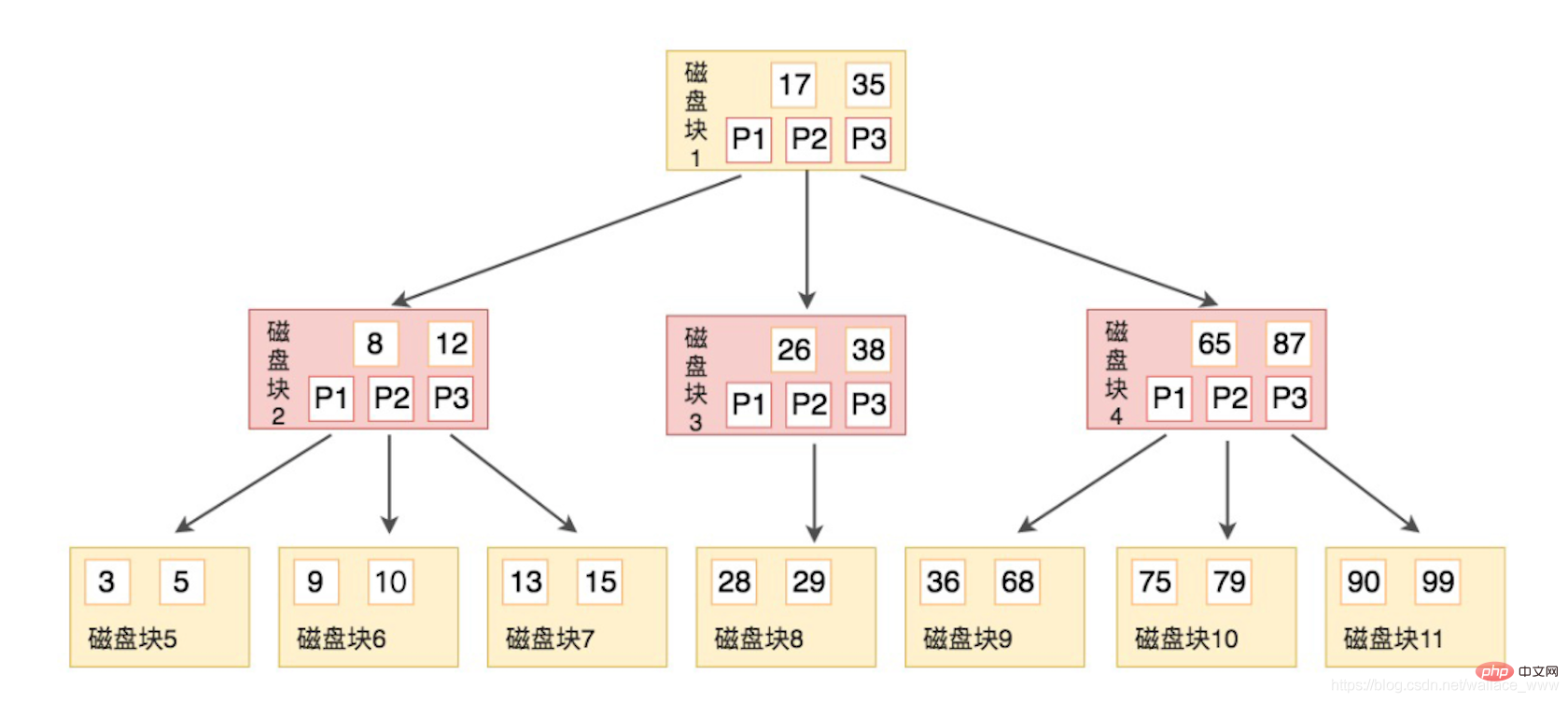
Angenommen, wir möchten jetzt 9 finden, sind die Schritte wie folgt:

Vergleichen Sie Block 1 (17,35) mit dem Stammknoten der Festplatte. Er ist kleiner als 17. Suchen Sie weiter im Zeiger P1, der der Festplatte entspricht Block 2

1. und Plattenblock 2 (8 ,12) Vergleichen Sie, befindet sich zwischen den beiden, suchen Sie weiter am Zeiger P2, der Plattenblock 6 entspricht
2. und vergleichen Sie mit Plattenblock 6 (9, 10), Sie können das sehen 9
3. Obwohl viele Vergleichsvorgänge durchgeführt wurden, wird der Vergleich innerhalb des Festplattenblocks im Speicher durchgeführt, wodurch keine Festplatten-E/A verbraucht wird. Der obige Vorgang erfordert nur 3 E/A. Os zu vervollständigen, was eine ideale Struktur ist.

B+-Baum-Index

Der B+-Baum wird auf Basis des B-Baums weiter verbessert. Der Unterschied zwischen B+-Baum und B-Baum ist wie folgt:

Der B+-Baum wird für die Schlüsselwörter im übergeordneten Knoten erstellt. Alle Schlüsselwörter des linken Teilbaums sind kleiner als dieser Wert und alle Schlüsselwörter des rechten Teilbaums sind größer oder gleich diesem Wert Der Knoten wird auch in den untergeordneten Knoten angezeigt und stellt den Maximalwert (oder Mindestwert) in den untergeordneten Knoten dar.

1. Alle Schlüsselwörter werden in den Blattknoten angezeigt, und die Blattknoten bilden eine geordnete verknüpfte Liste, sortiert von klein nach groß.
2. Das Beispiel sieht wie folgt aus:
3. Angenommen, Sie möchten das Schlüsselwort finden 16, die Suchschritte lauten wie folgt:

Vergleichen Sie mit Root-Knoten-Festplatte 1 (1,18,35), 16 liegt zwischen 1 und 18, holen Sie sich den Zeiger P1, der auf Festplatte 2 zeigt

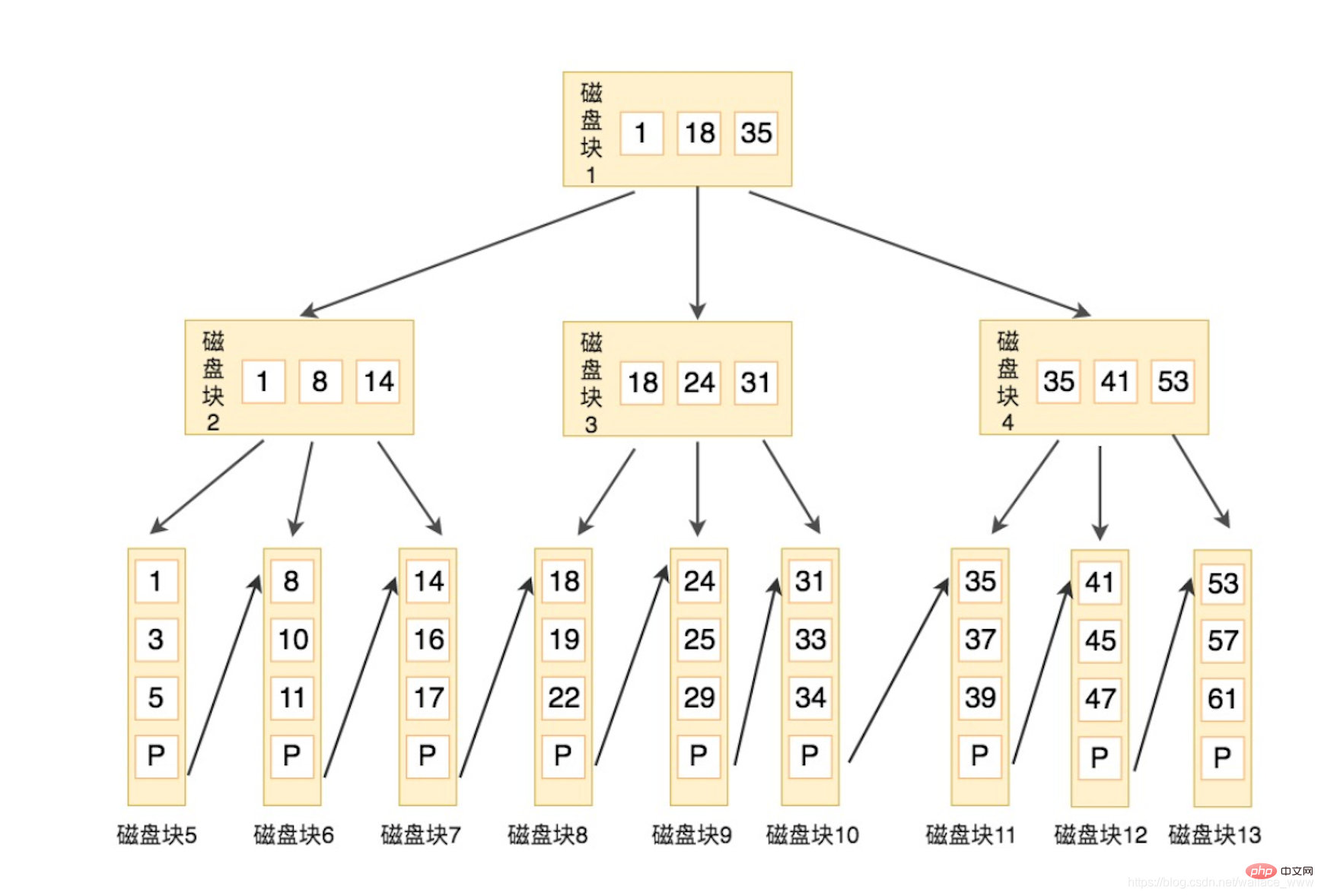Finden Sie Festplatte 2 (1,8 ,14), 16 ist größer als 14, holen Sie sich den Zeiger P3, der auf Datenträger 7 zeigt. Daher ist die Anzahl der Datensätze, die jeder interne Knoten speichern kann, viel größer als bei B Tree, die Baumhöhe ist niedriger, die E/A ist geringer und die von jedem E/A gelesene Datenseite enthält mehr Inhalt

Kann Bereichsabfragen unterstützen. Durchlaufen Sie einfach die geordnete verknüpfte Liste, die aus Blattknoten besteht. Alle Daten werden in Blattknoten gespeichert, sodass die Abfrageeffizienz stabiler ist. HASH-Index. Die Standardindexstruktur der Speicherspeicher-Engine von MySQL ist der Hash-Index Eine Funktion, sogenannte Hash-Funktion, die einen bestimmten Algorithmus (wie MD5, SHA1, SHA2 usw.) verwendet, um Eingaben beliebiger Länge in Ausgaben fester Länge umzuwandeln. Dieser Artikel wird nicht angegeben Eine ausführliche Einführung in die Hash-Funktion finden Sie in der Baidu-Enzyklopädie.

1. Hash-Sucheffizienz ist O(1), was sehr effizient ist. Pythons Diktat, Golangs Map und Javas Hash-Map werden alle auf Basis von Hash implementiert.
2. Für eine präzise Suche ist der Hash-Index effizienter als der B+-Baum-Index, aber der Hash-Index weist einige Einschränkungen auf, sodass er nicht die gängigste Indexstruktur ist.
3. Da die Daten, auf die der Hash-Index verweist, ungeordnet sind, kann der Hash-Index weder nach Bereichen abgefragt werden, noch unterstützt er die Sortierung ORDER BY.

Da Hash eine exakte Übereinstimmung ist, können keine Fuzzy-Abfragen durchgeführt werden.

Der Hash-Index unterstützt nicht das Prinzip der am weitesten links liegenden Übereinstimmung des gemeinsamen Index, und der gemeinsame Index wird nur wirksam, wenn eine vollständige Übereinstimmung vorliegt. Weil der Hash-Index den Hash-Wert berechnet, indem er die Indizes zusammenführt und dann den Hash-Wert zusammen berechnet, anstatt den separaten Hash-Wert jedes Index zu berechnen.
1. Wenn das indizierte Feld viele doppelte Werte enthält, führt dies zu einer großen Anzahl von Hash-Konflikten und die Abfrage wird sehr zeitaufwändig.
3. Aus den oben genannten Gründen unterstützt die MySQL-InnoDB-Engine keinen Hash-Index, aber es gibt eine adaptive Hash-Index-Funktion in der Speicherstruktur. Wenn ein bestimmter Indexwert sehr häufig verwendet wird, basiert er auf dem B+-Baum index
Erstellen Sie automatisch einen Hash-Index, um die Abfrageleistung zu verbessern.

Der adaptive Hash-Index kann als „Index von Indizes“ verstanden werden. Der Hash-Index wird verwendet, um die Seitenadresse im B+-Baumindex zu speichern und den entsprechenden Blattknoten schnell zu finden. Es kann über die Variable innodb_adaptive_hash_index angezeigt werden.

Empfohlenes Lernen: MySQL-Tutorial

Das obige ist der detaillierte Inhalt vonVertiefendes Verständnis der MySQL-Indexstruktur. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!