Beherrschen Sie den Deep-First-Algorithmus der JavaScript-Baumstruktur in einem Artikel

Dieser Artikel vermittelt Ihnen relevantes Wissen über Javascript und stellt hauptsächlich den JavaScript-Baumstruktur-Tiefen-First-Algorithmus vor. Man kann sagen, dass die Baumstruktur eine der häufigsten Datenstrukturen im Front-End ist, wie z. B. DOM-Baum und Kaskade Auswahl, Baumkomponente, schauen wir uns das an, ich hoffe, es wird für alle hilfreich sein.

【Verwandte Empfehlungen: Javascript-Video-Tutorial, Web-Frontend】

Was ist ein Baum?

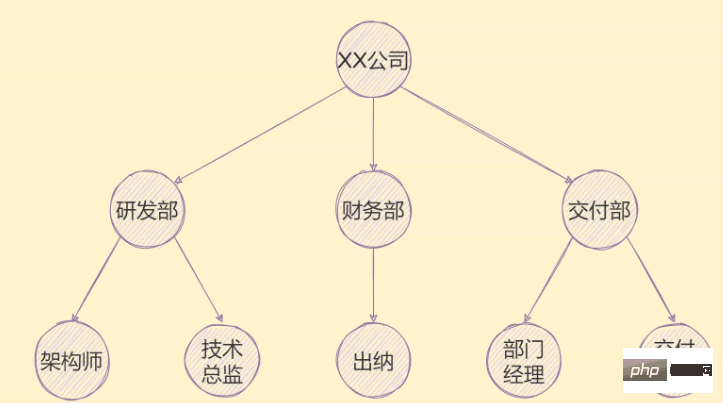
Im wirklichen Leben glaube ich, dass jeder mit Bäumen vertraut ist, egal ob Weiden, Pappeln oder Pfirsiche Bäume Man kann sagen, dass Bäume überall in unserem Leben zu sehen sind. In der Computerwelt ist ein Baum ein abstraktes Modell einer hierarchischen Struktur. Beispielsweise kann die Organisationsstruktur eines Unternehmens wie gezeigt dargestellt werden unten:

Neben der Organisationsstruktur können auch Genealogie, Provinzen und Städte usw. durch eine Baumstruktur dargestellt werden.

Baumterminologie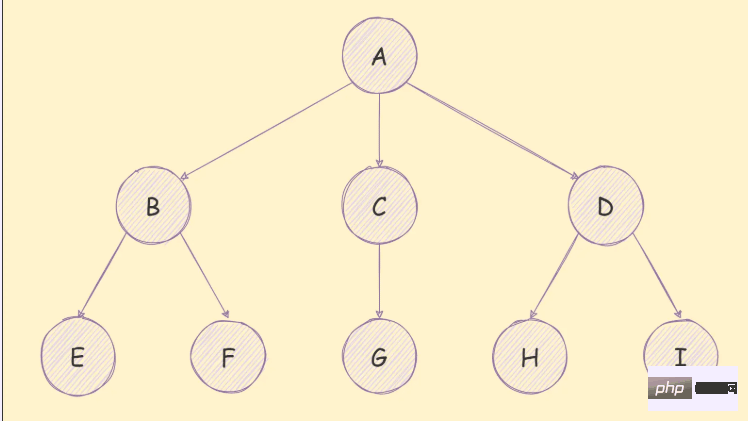

Baum hat viele Begriffe, wie unten gezeigt:

Baum

: eine endliche Menge von n (n≥0) Knoten, wenn n=0 , es wird ein leerer Baum genannt;

Der Grad des Knotens: Die Anzahl der

Teilbäume

des Knotens, zum Beispiel ist der Grad von Knoten B 2 und der Grad von Knoten A ist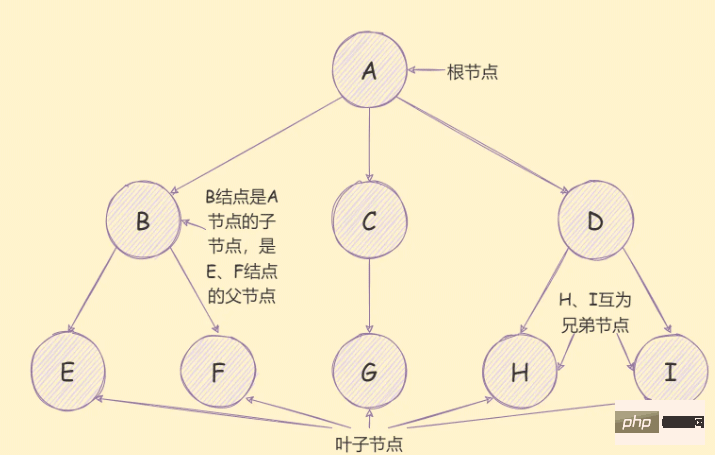

Der Grad des Baumes
• : Der maximale Grad unter allen Knoten des Baumes. Im Bild oben ist der Grad des Baumes beispielsweise 3; n=0时，称为空树；
• 节点的度：节点的子树个数，例如B节点的度就是2，A节点的度就是3；
• 树的度：树的所有节点中最大的度数，例如上图中，树的度是3；
• 叶子节点：度为0的节点，也叫叶节点；
• 子节点：如上图；
• 兄弟节点：如上图；
• 根节点：如上图；
• 树的深度：树中所有结点中的最大层次，例如上图中树的深度就是3；
• 节点的层次：例如E节点的层次就是3，节点的层次就是父节点层次+1，根节点的层次为1；
• 路径：一个节点到另一个节点的通道，例如A→H的路径就是A D H；
• 路径长度：一个节点到另一个节点的距离，例如A→H的路径就是3。

JavaScript中的树

树结构可以说是前端中最常见的数据结构之一，比如说DOM树、级联选择、树形组件等等；

JavaScript中并没有提供树这个数据结构，但是我们可以通过对象和数组来模拟一个树，

例如下面这段代码：

const tree = {
  value: 'A',
  children: [
    {
      value: 'B',
      children: [
        { value: 'E', children: null },
        { value: 'F', children: null },
      ],
    },
    {
      value: 'C',
      children: [{ value: 'G', children: null }],
    },
    {
      value: 'D',
      children: [
        { value: 'H', children: null },
        { value: 'I', children: null },
      ],
    },
  ],
}

广度优先和深度优点遍历算法

深度优先

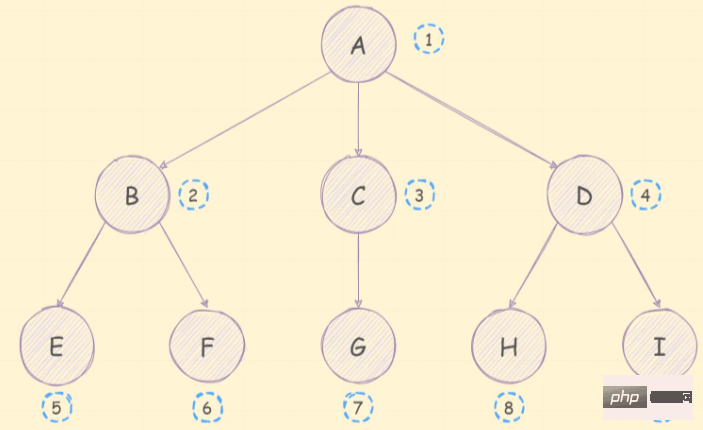
所谓的深度优先遍历算法，就是尽可能深的去搜索树的分支，它的遍历顺序如下图：

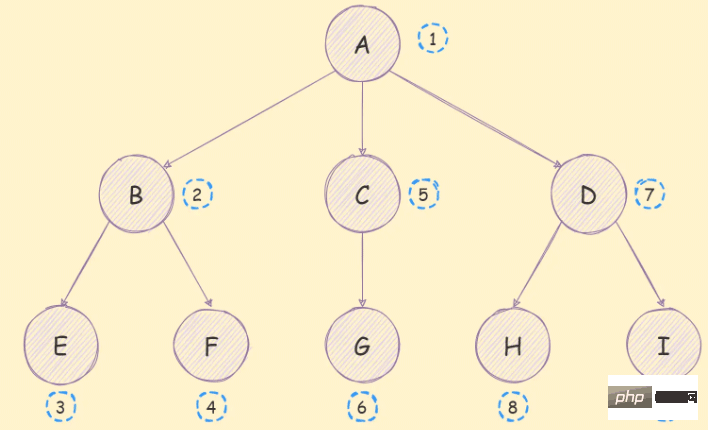
实现思路如下：

• 访问根节点；
• 对根节点的children持续进行深度优先遍历（递归）；

实现代码如下：

function dfs(root) {
  console.log(root.value)
  root.children && root.children.forEach(dfs) // 与下面一致
  // if (root.children) {
  //   root.children.forEach(child => {
  //     dfs(child)
  //   })
  // }
}
dfs(tree) // 这个tree就是前面定义的那个树
/* 结果
A
B
E
F
C
G
D
H
I
*/

可以看到，和图中的顺序是一致的，也就是说我们的算法没有问题。

广度优先

所谓的广度优先就是依次访问离根节点近的节点，它的遍历顺序如下图：

实现思路如下：

• 创建要给队列，把根节点入队；
• 把队头出队并访问；
• 把队头的childrenBlattknoten
:
• ein Knoten mit Grad 0

Kindknoten: Wie oben gezeigt;

Wurzelknoten

: Wie oben gezeigt; : Die maximale Ebene aller Knoten im Baum

, die Tiefe des Baums im Bild oben beträgt beispielsweise 3; die Ebene des Knotens: Die Ebene des E-Knotens beträgt beispielsweise 3 Die Knotenebene ist die übergeordnete Knotenebene + 1 und die Wurzelknotenebene ist

🎜Pfad🎜: 🎜Der Kanal von einem Knoten zu einem anderen Knoten 🎜, zum Beispiel ist der Pfad von A→H A D H; 🎜🎜🎜Pfadlänge🎜: 🎜Der Abstand von einem Knoten zu einem anderen Knoten🎜, zum Beispiel beträgt der Pfad von A→H 3. 🎜🎜🎜Baum in JavaScript🎜🎜Man kann sagen, dass die Baumstruktur eine der häufigsten Datenstrukturen im Front-End ist, wie z. B. DOM-Baum, kaskadierende Auswahl, Baumkomponente usw.; 🎜🎜Die Baumdatenstruktur ist Wird in JavaScript nicht bereitgestellt, aber wir können einen Baum durch Objekte und Arrays simulieren. 🎜🎜🎜Zum Beispiel der folgende Code: 🎜🎜

function bfs(root) {
  // 1. 新建队列 跟节点入队
  const q = [root]
  // 4 重复执行
  while (q.length > 0) {
    const node = q.shift() // 2 队头出队
    console.log(node.value)
    // 3 队头 children 依次入队
    node.children &&
      node.children.forEach(child => {
        q.push(child)
      })
  }
}
bfs(tree)
/* 结果
A
B
C
D
E
F
G
H
I
*/

🎜Breadth-First- und Depth-Advantage-Traversal-Algorithmus🎜🎜Depth-First🎜🎜🎜Der so- Der sogenannte Tiefendurchquerungsalgorithmus besteht darin, die Zweige des Baums so tief wie möglich zu durchsuchen. Seine Durchlaufsequenz ist wie folgt: 🎜🎜🎜🎜🎜🎜Die Implementierungsidee lautet wie folgt: 🎜🎜🎜🎜Besuchen Sie den Wurzelknoten; 🎜🎜Weitere Tiefendurchquerung (Rekursion) von die Wurzel children des Knotens; 🎜🎜🎜🎜Der Implementierungscode lautet wie folgt:🎜🎜rrreee🎜Sie können sehen, dass die Reihenfolge mit dem Bild übereinstimmt, was bedeutet, dass es kein Problem mit unserem Algorithmus gibt. 🎜🎜Breitenpriorität🎜🎜🎜Die sogenannte Breitenpriorität besteht darin, die Knoten zu besuchen, die dem Wurzelknoten am nächsten liegen, und zwar in der folgenden Reihenfolge: 🎜🎜🎜🎜🎜🎜Die Implementierungsidee lautet wie folgt: 🎜🎜🎜🎜Erstellen Sie eine Warteschlange und fügen Sie den Stammknoten zur Warteschlange hinzu; 🎜 🎜Entfernen Sie den Kopf der Warteschlange und greifen Sie darauf zu. 🎜🎜Fügen Sie die untergeordneten Elemente an der Spitze der Warteschlange der Reihe nach hinzu. 🎜🎜Wiederholen Sie die Schritte 2 und 3, bis die Warteschlange leer ist. 🎜🎜🎜🎜Der Implementierungscode lautet wie folgt: 🎜🎜rrreee🎜Wie Sie sehen können, stimmt er mit der Reihenfolge im Bild überein, was bedeutet, dass es kein Problem mit unserem Algorithmus gibt. 🎜🎜【Verwandte Empfehlungen: 🎜Javascript-Video-Tutorial🎜, 🎜Web-Frontend🎜】🎜

Das obige ist der detaillierte Inhalt vonBeherrschen Sie den Deep-First-Algorithmus der JavaScript-Baumstruktur in einem Artikel. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!